强化学习之基于伪计数的探索算法
©作者|王治海
学校|中国科学技术大学硕士生
研究方向|强化学习与机器博弈
强化学习基于智能体与环境的交互,以最大化累积奖励为目标,学习状态到动作的映射(即策略)。本文将主要围绕强化学习中的探索问题展开,首先介绍强化学习中的探索问题,并针对此问题介绍基于伪计数的探索算法,从核心思想和算法有效原因两个角度对该算法进行了深入的分析与讨论。
强化学习中的探索问题介绍
强化学习(Reinforcement Learning)
强化学习用于解决序贯决策问题,而该类问题往往通过马尔可夫决策过程(Markov Decision Process)进行建模。该过程可以通过五元组 表示。其中
表示状态空间,假设状态空间连续。
表示动作空间,假设动作空间连续。
是状态转移的概率密度函数。
是奖励函数。
表示折扣因子,是一个常数。
接下来将介绍强化学习算法面临的一个重要挑战,探索与利用困境。
探索与利用困境(Exploration and Exploitation Dilemma)
何为探索与利用困境
探索与利用困境是强化学习算法的一个重要挑战。直观的例子是今天小明想去吃顿好的,现在他有两家饭店A,B可以选择,A饭店是吃过一次的店,体验还不错,B饭店是新开张的店,B饭店有可能物美价廉,也有可能又贵又难吃。摆在小明面前的选择难题就是探索与利用困境。如果小明倾向于「利用」自己已有的信息,则会选择A饭店;如果小明倾向于「探索」自己不确定的动作,则会选择尝试B饭店。
图1. 小明选择饭馆吃饭(图片来源:UC Berkeley CS188 Intro to AI 课程ppt)在对环境未知的情况下,智能体通过与环境交互,即尝试A 饭店或者B 饭店,收集关于环境的信息。智能体应该基于已有的经验选择自认为最优的动作,如小明选择A饭店;还是去选择智能体不确定度高的动作,如小明尝试B饭店,便是探索与利用困境。
如果智能体只利用,则由于信息的不完整性,智能体很有可能陷入次优策略,如上例中B 饭店远优于A 饭店;如果智能体均匀随机盲目探索,则依旧会访问已经确认是低奖励的状态动作对,增加低质量的样本数量,如上例中小明分别去过4次A 饭店和B 饭店,几乎确认B 饭店体验极差,而如果小明均匀随机盲目探索,则还是会尝试B 饭店。因此,强化学习算法需要考虑如何平衡探索与利用,高效的探索环境,降低对环境的不确定性。接下来将介绍一种高效探索的原则——面向不确定度的乐观探索(Optimism in the Face of Uncertainty)。
面向不确定度的乐观探索(Optimism in the Face of Uncertainty)
何为不确定度(Uncertainty)
不确定度是涉及不完美或者未知信息时的认知情况。如小明在十八岁那一年高考750分和获得750万现金二选一,小明该如何决策。相信很多读者都没法直接给出决策,因为选择高考750分的未来发展的信息几乎未知,这个选择涉及非常高的不确定度,可能“一战封神“,也可能如仲永泯然众人。
深度学习领域中能够建模的不确定度主要有两种类别:偶然不确定度和认知不确定度[5][7]。
在强化学习中偶然不确定度产生于环境本身的随机性,认知不确定度的主要来源是因为收集的数据量不足而导致的不确定度。认知不确定度的特点是随着数据收集越来越多,不确定度会越来越小,直至0。如智能体走迷宫,在智能体没有充分的和环境交互之前,迷宫终点附近的数据量不足,智能体对于迷宫终点附近的认知不确定度高,这些地点可能有宝藏,也可能有陷阱。
以下通过例子给出一种数学建模认知不确定度的方式。
「例子:」 给定一个单状态单动作问题,定义奖励为随机变量 ,服从分布 , 为 区间上的未知分布。假设已经独立采集4个样本 ,我们希望去估计 ,一种常用的估计器 是使用样本均值估计,即 ,但是我们对于 的估计是不确定的,这个不确定度的大小可以由置信区间给出。给定置信度90%,应用霍夫丁不等式(Hoeffding's inequality),我们可得
注意其中 ,可以求得 有至少90%的概率落入区间 ,此时对于随机变量 均值的估计的不确定度的度量为 。这类对于随机变量均值的估计的不确定度属于认知不确定度,因为随着收集的数据量趋于无穷,相应不确定度会趋于0 (大数定理)。
面向不确定度的乐观探索
直观来说,面向不确定度的乐观探索是一个探索原则,即智能体倾向于探索不确定度高的状态动作对,以便确认这些状态动作对是否具备高奖励。智能体对于环境的不确定度可以由 度量[2], 为常数(离散状态离散动作问题设置, 代表状态动作对 被访问的次数)。具体推导细节由于篇幅限制在此不展开叙述,感兴趣的同学可以参考文献[2]。至此,基于计数的探索算法呼之欲出,具体地,将 作为奖励函数的额外奖励,即用于训练智能体的奖励为
直觉解释为如果智能体访问一个状态动作对越少,即 越小,对应的额外奖励 越大,智能体应该更倾向于访问这个状态动作对,确认这个状态动作对是否会是高奖励状态动作对。
但是基于计数的探索算法依赖于统计访问过的状态动作对的次数,这限制了其在连续状态空间下的应用。因为连续状态空间问题中,访问过的状态动作对几乎不会重复, 在大部分状态动作对下都是零,无法起到指导探索的作用。针对于连续状态空间设置下的问题,下文介绍一种基于「伪计数(pseudo-count)」 的探索算法[1]。
基于伪计数的探索算法
算法基本思想
在连续空间问题下,直接对状态动作对计数将失效,所以基于「伪计数(pseudo-count)」 的探索算法通过设计密度模型(density model)来评估状态出现的频率,从而计算伪计数 替代真实计数 ,将 作为奖励函数的额外奖励,即训练智能体的奖励为
何为伪计数
为了简化推导,假设只考虑状态的计数。假定状态空间为集合 ,给定已经访问过的状态信息 , 学习密度模型 评估状态 出现的频率,其中 为模型参数。该密度模型应该满足以下几个性质:
(1)输出总是非负,即 。
(2)对于没有见过且与 都不相似的状态,输出接近于0。
(3)对于出现过或者与 中的状态比较相似,输出较高的值。
在智能体收集到新样本 后,历史数据更新为 ,密度模型也会更新为 ,密度模型的更新方式可以参考文献[4]。基于密度模型,模拟计数特性,依据频率逼近概率的思想,定义伪计数函数 和伪计数总数 ,
也就是说,我们希望在观察到一个数据 后,密度模型预测的 的概率密度会上升,反映到伪计数函数上为相应伪计数增长1,即。由此联立方程可求出
为了使得伪计数符合我们的直觉,它需要满足 ,因此,密度模型需要满足性质:
(4)对于每次收集到任意新样本 时,满足 。即数据 出现的频率增加,密度模型预测 的概率密度上升。
综上,只要有能够满足以上4点性质的密度模型,则可以估计伪计数 ,从而利用伪计数指导探索。具体密度模型的实现方式见文献[4]。
注意,以上定义能方便地拓展延伸到计数状态动作对的情况,即 。
算法流程
以下是基于伪计数探索算法的伪代码,由于论文中没有给出相应的伪代码,我根据自己的理解列出了该算法基本的流程。
图2. 基于伪计数的探索算法伪代码算法有效的原因
该算法有效的主要原因在于以下两点:理论启发,在表格问题设置下,前人证明了 可以作为智能体对环境的不确定度,将 加入奖励函数,可以保证高效探索;在连续空间问题下,该算法设计的伪计数函数具备泛化性的同时能有效反映真实计数的变化情况。
「(1)理论启发: 作为探索额外奖励符合直觉且具备理论保证。」 该算法沿袭了算法Model Based Interval Estimation with Exploration Bonus(MBIE-EB)[2] 的思路。从理论角度看,在表格的问题设置下,MBIE-EB从理论上推导出了 可以度量智能体对环境的不确定度。因此,「如果伪计数 能够有效反映真实计数 ,」 则可以近似认为 也可以度量智能体对环境的不确定度,将 加入奖励函数,依旧可以保证高效探索。从直觉角度看,如果智能体访问一个状态动作对越少,则计算出来的 越小,智能体应该更倾向于去访问这个状态动作对,确定这个状态动作对是否会是高奖励状态动作对,即对应的额外奖励 越大。
「(2)伪计数具备泛化性的同时能有效反映真实计数的变化情况,即伪计数和真实计数在总体趋势上成正相关关系。」 论文[1] 中的Figure 1展示了Atari 游戏环境FREEWAY 环境中使用连续密度模型计算的伪计数和真实计数有较强正相关关系。也就是图3,右侧是FREEWAY 游戏环境,游戏任务是控制一只小鸡过马路,在过马路的过程中可能会被小车撞击导致倒退。小鸡被初始化在马路的一边,目标是控制小鸡到达马路对边。左侧曲线横轴代表和环境交互的步数,纵轴代表伪计数。黑色曲线代表小鸡初始化的位置对应的伪计数、变化趋势是持续正向增加,和真实发生的次数的变化趋势一致。绿色曲线代表小鸡到达马路对面对应的伪计数,淡绿色区域对应的时间段内,小鸡到达了马路对面,伪计数变化趋势是迅速增加,而在小鸡还没有到达过马路对面时,其伪计数接近于0。
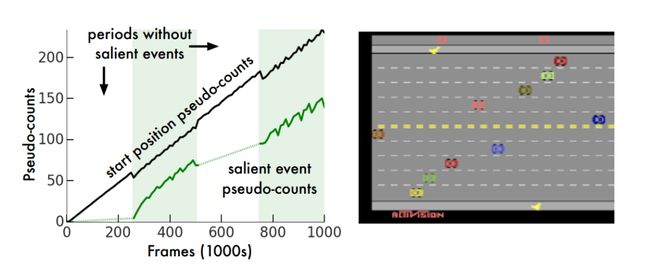 图3. FREEWAY 环境伪计数变化趋势图示 [1]
图3. FREEWAY 环境伪计数变化趋势图示 [1]
研究思路分析
本文介绍的基于伪计数的探索算法由论文[1] 提出,而这篇论文研究科学问题的思路有许多值得借鉴之处,故在这一章节专门针对论文[1] 的研究思路进行总结与分析。
(1)理论启发。在有限马尔科夫决策过程中,基于计数指导探索的思路具备理论保证,从而启发在连续控制问题中使用相关技术去近似计数。
(2)方法以性质为导向。论文[1] 提出了求取伪计数的一种思路之后,围绕伪计数直觉上应该满足的性质进行分析与验证,从而使得方法有效的原因更加清晰。
总结
本文针对于强化学习中的高效探索问题介绍了一种基于伪计数的探索算法。首先介绍了强化学习和探索与利用困境。然后给出解决如何高效探索问题的算法——基于伪计数的探索算法。分析了该算法的基本思想和有效的原因。该算法的基本思想来自于表格环境下的基于计数的探索算法,但是基于计数的探索算法依赖于统计访问过的状态动作对的次数,而连续状态空间问题中,访问过的状态动作对几乎不会重复, 在大部分状态动作对下都是零,无法起到指导探索的作用。因此,该算法通过设计满足一定性质的密度模型来评估频次,计算在连续空间下具有泛化性的伪计数鼓励探索。最后,本文分析了提出基于伪计数的探索算法的论文的研究思路。
参考文献
[1] Bellemare M, Srinivasan S, Ostrovski G, et al. Unifying count-based exploration and intrinsic motivation[C] Advances in neural information processing systems. 2016: 1471-1479.
[2] Strehl A L, Littman M L. An analysis of model-based interval estimation for Markov decision processes[J]. Journal of Computer and System Sciences, 2008, 74(8): 1309-1331.
[3] THEREFORE STOC, ASM. Guide to the Expression of Uncertainty in Measurement[J]. 1993.
[4] Bellemare M, Veness J, Talvitie E. Skip context tree switching[C] International Conference on Machine Learning. 2014: 1458-1466.
[5] Kendall A, Gal Y. What uncertainties do we need in bayesian deep learning for computer vision?[C] Advances in neural information processing systems. 2017: 5574-5584.
[6] Brockman G, Cheung V, Pettersson L, et al. Openai gym[J]. arXiv preprint arXiv:1606.01540, 2016.
[7] Clements W R, Robaglia B M, Van Delft B, et al. Estimating risk and uncertainty in deep reinforcement learning[J]. arXiv preprint arXiv:1905.09638, 2019.
作者简介:
王治海,2020年毕业于华中科技大学电气与电子工程学院,获得工学学士学位。现于中国科学技术大学电子工程与信息科学系的 MIRA Lab 实验室攻读研究生,师从王杰教授。研究兴趣包括强化学习与机器博弈。
????
现在,在「知乎」也能找到我们了
进入知乎首页搜索「PaperWeekly」
点击「关注」订阅我们的专栏吧
关于PaperWeekly
PaperWeekly 是一个推荐、解读、讨论、报道人工智能前沿论文成果的学术平台。如果你研究或从事 AI 领域,欢迎在公众号后台点击「交流群」,小助手将把你带入 PaperWeekly 的交流群里。