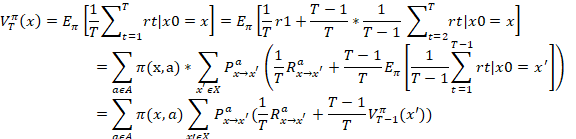强化学习与深度强化学习理解

强化学习

主要参考西瓜书和一些网上视频加上个人理解，欢迎互动。

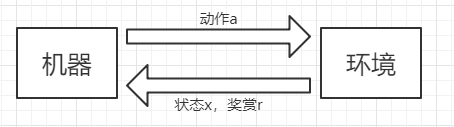
强化学习的model如下图所示，机器在当前状态下做出动作a，然后环境反馈给机器下一个状态和一个奖励。

​

假定状态空间X，每一个状态x∈X，动作空间A，每一个动作a∈A，奖赏函数为R，P为状态转移函数，那么强化学习对应了四元组E=。此处以西瓜浇水为例：

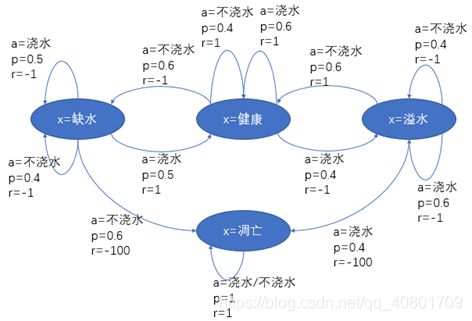
机器通过在环境中不断尝试来学得一个最优的“策略”π。策略有两种表示方法：一种是将策略表示为函数π：X->A，确定性策略常用这种表示；另一种是概率表示π：X，A->R，随机性策略常用这种表示，π(x, a)表示为状态x下选择动作a的概率，且。[确定性策略是指在状态x下，动作是唯一确定的]。另外上图摘自西瓜书，个人觉得在采取随机策略下，x=缺水下a=浇水和a=不浇水概率之和应该为1，此处不是很理解。

强化学习与监督学习的异同

若将“状态”对应监督学习中的“示例”，“动作”对应为“标记”，则可看出强化学习的“策略”相当于监督学习中的“分类器”，相当于神经网络中的修改连接权值W。先提前了解一下，如下图所示：

K-摇臂赌博机

提出了探索和利用两个概念。“仅探索”指将所有的尝试机会平均分配给每个摇臂，最后计算每个摇臂平均吐币数作为奖赏近似。“仅利用”指按下目前为止平均奖赏最大的摇臂。“仅探索”能很好估计每个摇臂的奖赏，却会失去很多选择最优摇臂机会，“仅利用”没有很好的估计摇臂期望奖赏，可能经常选不到最优摇臂。

ε-贪心

ε-贪心法很简单但很实用，是对探索和利用的折中，平时编程经常对随机探索和启发式挖掘做均衡，都差不多。每次尝试时都以ε的概率进行探索，即以均匀概率随机选择一个摇臂；以1-ε概率利用，即选择当前平均奖赏最高的摇臂。此处需要了解一下平均累计奖赏更新：

此处，Q表示奖赏函数，k表示第k个摇臂，n表示第几次，v表示第n次摇k臂获得的奖赏。

实际中ε一般设为指数衰减函数，后期进行过多的探索会产生很多不需要的计算量，就像摇臂机摇10000的期望奖赏已经接近实际值了。

Softmax算法

也是用来完成对探索和利用的折中，基于Boltzmann分布分配。

P(k)表示每个摇臂被选到的概率，t趋于0为“仅利用”，t趋于无穷为“仅探索”。Boltzmann分布用处很广，感兴趣可以多google，此处我没试过，不知道效果怎么样。

有模型学习

假定任务对应的马尔科夫决策过程四元组E=均已知。此时，对任意状态x和x’和动作a，在x状态下执行动作a转移到x’状态的概率是已知的，该转移带来的奖赏也是已知的。

在模型已知时，对任意策略π能估计出该策略带来的期望累计奖赏。令函数表示从状态x出发，使用策略π所带来的累计奖赏；函数表示从状态x出发，执行动作a后再使用策略π带来的累计奖赏。

“策略”是通过在环境中不断尝试而学得，根据策略，在状态x下就能得知要执行的动作a=π(x)，当然如上所说，经常返回概率，表示执行不同动作的可能性。

由累计奖赏定义，有状态值函数：

状态动作值函数如下：

由于MDP(有模型学习)具有马尔科夫性，系统下一时刻状态仅由当前时刻状态决定，不依赖以往状态，所以值函数有简单的递归形式：

这个推导数公式的理解关键在于第二步，这是一个简单的全概率展开，此处采用的是上面所说的随机性策略,并且假定执行的动作为a。如此之后x状态转变为x’，表示在执行完动作a后返回状态x’的概率。此处强烈建议参考西瓜浇水图理解【本文第二个图片】。

类似的，对于γ折扣累计奖赏有：

如果观察细心，会发现和的后半部分即状态动作值函数。

'

所有的推导关键是为了推出递归式，学过算法导论应该理解，递归可以用迭代解，也可以用动态规划解，可以简化计算，目的也就实现了。

策略改进

理想的策略应该能最大化累计奖赏，即

所以以上的迭代也应该替代为最优迭代，即

上式均为最优Bellman等式，其唯一解是最优值函数。

从上面推到和算法分析过程可知，在模型已知时强化学习任务能归结为基于动态规划的寻优问题。

免模型学习

若学习算法不依赖于环境建模，则称为“免模型学习”。

蒙特卡罗强化学习

简单理解：多次“采样”，然后求取平均累计奖赏来作为期望累计奖赏的近似。

简单实现：在模型未知的情形下，我们从起始状态出发，使用某种策略进行采样，执行该策略T步并获得轨迹

然后，对轨迹上出现的每一对状态-动作，记录其后的奖赏之和，作为该状态-动作对的一次累计奖赏采样值。对多条轨迹进行采样后，将每个状态-动作对的累计奖赏采样值进行平均，即得到状态-动作值函数的估计。

同样采用增量式计算，每采样出一条轨迹，就根据该轨迹涉及的所有“状态-动作”对来对值函数进行更新，即

时序差分学习

蒙特卡罗强化学习算法的本质，是通过多次尝试后求平均来作为期望累计奖赏的近似，但它在求平均时是“批处理式”进行的，即在一个完整的采样轨迹完成后再对所有的状态-动作对进行更新。实际上这个更新过程能增量式进行。对于状态-动作对(x,a)，不妨假定基于t个采样已估计出值函数，则在得到第t+1个采样时，有

更一般的，将替换成一个较小的正整数α，跟新步长越大，则越靠后的累积奖赏越重要。

无穷多个状态的解决

不妨直接对连续状态空间进行学习。假定状态空间为n维实数空间X=,此时难以用表格值函数来记录，先考虑简单情形，即值函数能表达成线性函数，即

其中x为状态向量，为参数向量，此时的值函数难以精确记录每个状态的值，因此采用值函数近似，最常用的肯定就是最小二乘法了。即

为使误差最小，采用梯度下降法，关于梯度下降法可以参考BP神经网络。

对于复杂的情形，线性函数估计不能达到理想的结果，这也就有了深度强化学习DQN。

模仿学习

此处直接以DQN为例，简单理解：先提供一些专家数据，可以理解为带标签的数据，进行监督学习，学得一个初始策略，然后在输入其它情形对反馈进行改进，获得更好的决策。

逆强化学习

与模仿学习类似，从人类专家提供的范例数据中反推出奖赏函数有助于解决问题。

深度强化学习

深度强化学习DQN简单可以用如下图来进行表示，即

DQN实现代码：

def trainNetwork(s, readout, h_fc1, sess):
	# s作为输入，readout作为输出
    # define the cost function
    a = tf.placeholder("float", [None, ACTIONS])
    y = tf.placeholder("float", [None])
    readout_action = tf.reduce_sum(tf.multiply(readout, a), reduction_indices=1)  # a=[0,1] or [1,0]
    cost = tf.reduce_mean(tf.square(y - readout_action))
    train_step = tf.train.AdamOptimizer(1e-6).minimize(cost)  # Aim

    # open up a game state to communicate with emulator
    game_state = game.GameState()

    # store the previous observations in replay memory
    D = deque()

    # printing
    a_file = open("logs_" + GAME + "/readout.txt", 'w')
    h_file = open("logs_" + GAME + "/hidden.txt", 'w')

    # get the first state by doing nothing and preprocess the image to 80x80x4
    do_nothing = np.zeros(ACTIONS)
    do_nothing[0] = 1
    x_t, r_0, terminal = game_state.frame_step(do_nothing)
    x_t = cv2.cvtColor(cv2.resize(x_t, (80, 80)), cv2.COLOR_BGR2GRAY)
    ret, x_t = cv2.threshold(x_t,1,255,cv2.THRESH_BINARY)  # 黑白二值化
    s_t = np.stack((x_t, x_t, x_t, x_t), axis=2)

    # saving and loading networks
    saver = tf.train.Saver()
    sess.run(tf.initialize_all_variables())
    checkpoint = tf.train.get_checkpoint_state("saved_networks")
    if checkpoint and checkpoint.model_checkpoint_path:
        saver.restore(sess, checkpoint.model_checkpoint_path)
        print("Successfully loaded:", checkpoint.model_checkpoint_path)
    else:
        print("Could not find old network weights")

    # start training
    epsilon = INITIAL_EPSILON
    t = 0
    while "flappy bird" != "angry bird":
        # choose an action epsilon greedily
        readout_t = readout.eval(feed_dict={s : [s_t]})[0]  # 此处值函数通过不断积累经验估计出来的
        a_t = np.zeros([ACTIONS])  # 动作
        action_index = 0
        if t % FRAME_PER_ACTION == 0:
            if random.random() <= epsilon:
                print("----------Random Action----------")
                action_index = random.randrange(ACTIONS)
                a_t[random.randrange(ACTIONS)] = 1
            else:
                action_index = np.argmax(readout_t)
                a_t[action_index] = 1
        else:
            a_t[0] = 1 # do nothing

        # scale down epsilon
        if epsilon > FINAL_EPSILON and t > OBSERVE:
            epsilon -= (INITIAL_EPSILON - FINAL_EPSILON) / EXPLORE

        # run the selected action and observe next state and reward
        x_t1_colored, r_t, terminal = game_state.frame_step(a_t)  # 返回状态和reward
        x_t1 = cv2.cvtColor(cv2.resize(x_t1_colored, (80, 80)), cv2.COLOR_BGR2GRAY)
        ret, x_t1 = cv2.threshold(x_t1, 1, 255, cv2.THRESH_BINARY)
        x_t1 = np.reshape(x_t1, (80, 80, 1))
        #s_t1 = np.append(x_t1, s_t[:,:,1:], axis = 2)
        s_t1 = np.append(x_t1, s_t[:, :, :3], axis=2)

        # store the transition in D
        D.append((s_t, a_t, r_t, s_t1, terminal))
        if len(D) > REPLAY_MEMORY:
            D.popleft()

        # only train if done observing
        if t > OBSERVE:  
            # sample a minibatch to train on
            minibatch = random.sample(D, BATCH)

            # get the batch variables
            s_j_batch = [d[0] for d in minibatch]
            a_batch = [d[1] for d in minibatch]
            r_batch = [d[2] for d in minibatch]
            s_j1_batch = [d[3] for d in minibatch]

            y_batch = []
            readout_j1_batch = readout.eval(feed_dict = {s : s_j1_batch})
            for i in range(0, len(minibatch)):
                terminal = minibatch[i][4]
                # if terminal, only equals reward
                if terminal:
                    y_batch.append(r_batch[i])  # 结束
                else:
                    y_batch.append(r_batch[i] + GAMMA * np.max(readout_j1_batch[i]))  # 累计reward

            # perform gradient step
            train_step.run(feed_dict = {
                y : y_batch,  # reward
                a : a_batch,  # 动作
                s : s_j_batch} # 图片状态
            )

        # update the old values
        s_t = s_t1  # 下一状态
        t += 1

        # save progress every 10000 iterations
        if t % 10000 == 0:
            saver.save(sess, 'saved_networks/' + GAME + '-dqn', global_step = t)

        # print info
        state = ""
        if t <= OBSERVE:
            state = "observe"
        elif t > OBSERVE and t <= OBSERVE + EXPLORE:
            state = "explore"
        else:
            state = "train"

        print("TIMESTEP", t, "/ STATE", state, \
            "/ EPSILON", epsilon, "/ ACTION", action_index, "/ REWARD", r_t, \
            "/ Q_MAX %e" % np.max(readout_t))
        # write info to files
        '''
        if t % 10000 <= 100:
            a_file.write(",".join([str(x) for x in readout_t]) + '\n')
            h_file.write(",".join([str(x) for x in h_fc1.eval(feed_dict={s:[s_t]})[0]]) + '\n')
            cv2.imwrite("logs_tetris/frame" + str(t) + ".png", x_t1)
        '''

 完整代码链接：

https://github.com/yenchenlin/DeepLearningFlappyBird