吴恩达机器学习 2022新版
2022吴恩达机器学习 第一周
- 一. 机器学习的定义
- 二. 机器学习的分类
-
- 2.1. 监督学习
-
- 【回归算法】
- 【分类算法】
- 三. loss function
-
- 3.1.损失函数公式
- 四. 梯度下降
-
- 4.1.梯度下降算法
- 4.2.理解梯度下降
- 4.3.学习率的选择
- 4.5.如何计算导数项?
一. 机器学习的定义
Arthur Samuel(1959)在没有明确设置的情况下,使计算机具有学习能力的研究领域。
Field of study that gives computers the ability to learn without being explicitly programmed.
Tom Mitchell(1998)假设用P来评估计算机程序在某任务类T上的性能,若一个程序通过利用经验E在T中任务上获得了性能改善,则我们就说关于T和P,该程序对E进行了学习。
Well-posed Learning Problem: A computer program is said to learn from experience E with respect to some task T and some performance measure P, if its performance on T, as measured by P, improves with experience E.
二. 机器学习的分类
监督学习(supervised learning)和无监督学习(unsupervised learning)
Q.监督学习和无监督学习划分依据?
- 根据训练数据是否拥有标记信息(data labeled or not)
- 监督学习数据同时带有输入x和输入标签y,无监督学习数据仅带有输入x但不输出标签y
- 无监督学习算法必须找到数据中的某种结构或某种模式
2.1. 监督学习
监督学习指的是学习x到y或输入到输出映射的算法。监督学习的关键特征是你给予学习算法示例。这包括正确的答案,对于给定的输入x,正确的标签y是通过查看正确的学习算法最终学习到的输入x和期望的输出标签y,只取输入而没有输出标签并给出对输出的合理准确的预测或猜测。
【回归算法】
回归定义
Regression 就是找到一个函数 function ,通过输入特征 x,输出一个数值 Scalar。
应用举例
【经典房价预测】
我们给算法一个数据集,所谓的正确答案,那就是为地块上的每所房子给出的标签或正确的价格y,学习算法的任务是产生更多这样的正确答案,具体预测什么是可能的价格。
【线性回归模型】
给定数据集D={(x1,y1),(x2,y2),…,(xm,ym)},其中xi=(xi1;xi2;…;xid),yi∈R.
“线性回归”试图学得一个线性模型以尽可能准确地预测实值输出标记。
f(xi)=wxi+b
【分类算法】
分类定义
在分类中,学习算法必须对一个类别进行预测,所有可能的输出都是一小组
应用举例
乳腺癌检测-预测类别或离散类别
Q.回归任务和分类任务的不同之处?
- 分类只有少数可能的输出,所以有一个离散的,可能的输出的有限集合。
- 回归问题中模型可以输出无限多可能的数字
三. loss function
loss function 损失函数 cost function 代价函数
-
优化问题->最小化损失函数
-
回归任务中衡量一条线与训练数据的拟合程度
Model: fw,b(x)=wx+b
模型:x,输入或输入特征;函数y称为模型;y’为模型的预测
w,b:参数、系数、权重。slop斜率
Q.如何建立模型?
- step1:模型假设,选择模型框架(eg. 线性模型)
- step2:模型评估,如何判断众多模型的好坏(损失函数)
- step3:模型优化,如何筛选最优的模型(梯度下降)
3.1.损失函数公式
均方误差函数,通常用于线性回归
J ( w , b ) = 1 2 m ∑ i = 1 m ( y ^ − y ) 2 J_{(w,b)}=\frac{1}{2m} \sum_{i=1}^m(\hat{y}-y )^2 J(w,b)=2m1i=1∑m(y^−y)2
J ( w , b ) = 1 2 m ∑ i = 1 m ( f w , b ( x i ) − y i ) 2 J_{(w,b)}=\frac{1}{2m}\sum_{i=1}^m(f_{w,b}(x^i)-y^i)^2 J(w,b)=2m1i=1∑m(fw,b(xi)−yi)2
J(w,b)是关于w,b的函数,w控制由下式定义的线的斜率
代价函数的极值找对应的参数, choose w,b to minimize(w)
J是衡量平方误差有多大的成本函数,所以选择最小化这些平方误差的w,使它们尽可能小
在线性回归中如何使用成本函数来找到最小化J的w值
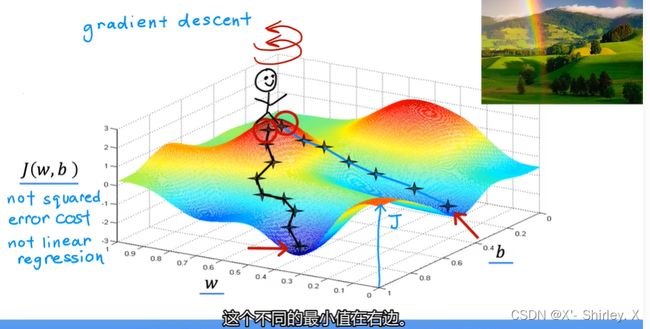
四. 梯度下降
尝试最小化任何函数,而不仅仅是线性回归的代价函数。适用于更一般的函数,包括与具有两个以上参数的模型一起使用的其他成本函数
底部轴w,b。z轴表示表面高度,为成本函数的值。离表面高度越高,代价函数值越高
-
寻找最快下山的途径=最陡下降方向
-
寻找到达谷底的最小值
Q.局部最小值和全局最小值?
- 一般来说,会有多个局部最小值而只有一个全局最小值
- 线性模型中,凸函数中一般只有一个局部最小也是全局最小值?
4.1.梯度下降算法
w = w − ∂ J ∂ w w=w-\frac{\partial_J}{\partial_w} w=w−∂w∂J
表示在你的参数w之后,取当前值w并对其进行少量调整,也就是右边的这个等式
两个参数同时更新
t m p w = w − ∂ J ∂ w tmp_w=w-\frac{\partial_J}{\partial_w} tmpw=w−∂w∂J
t m p b = b − ∂ J ∂ b tmp_b=b-\frac{\partial_J}{\partial_b} tmpb=b−∂b∂J
w = t m p w w=tmp_w w=tmpw
b = t m p b b=tmp_b b=tmpb
当你听到有人谈论梯度下降时,他们总是指你所在的梯度下降执行参数的同时更新
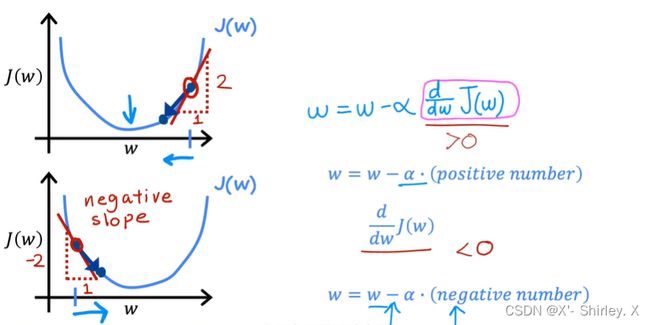
4.2.理解梯度下降
α称为学习率,通常介于0和1之间的一个小的正数,基本上控制你如何下坡迈出一大步,控制更新模型参数w和b时的步长

4.3.学习率的选择
-
当学习率太小时,需要很多步骤才能达到最低限度,梯度下降会起作用但非常慢,需要很长时间
-
当学习率太大时,结果会过冲并且可能永远不会达到最小值。大相交可能无法收敛,甚至可能发散
随着我们越来越接近局部最小梯度下降,将自动采取更小的步骤。因为我们接近局部最小值时,导数会自动变小,这意味着更新步骤也会自动变小,即使学习率保持在某个固定值。
如果此时参数已经使损失达到了局部最小值,那么不会有进一步的梯度下降,它将解决方案保持在该局部最小值,这也解释了为什么梯度下降可以达到局部最小值,即使使用固定的学习率
4.5.如何计算导数项?
1 m ∑ i = 1 m ( x i ) − y i ) x i \frac{1}{m}\sum_{i=1}^m(x^i)-y^i)x^i m1i=1∑m(xi)−yi)xi
J/w微分
1 m ∑ i = 1 m ( f w , b ( x i ) − y i ) \frac{1}{m}\sum_{i=1}^m(f_{w,b}(x^i)-y^i) m1i=1∑m(fw,b(xi)−yi)
1 m ∑ i = 1 m ( f w , b ( x i ) − y i ) \frac{1}{m}\sum_{i=1}^m(f_{w,b}(x^i)-y^i) m1i=1∑m(fw,b(xi)−yi)
事实证明,当使用带有线性回归的平方误差成本函数时,成本函数没有也永远不会有多个局部最小值,它有一个全局最小值,因为bowl shape,convex function。当在凸函数上实现梯度下降时,只要选择适当的学习率,它就始终收敛到全局最小值。
Q.什么是批量梯度下降?
指的是在梯度下降的每一步中,我们都在查看所有训练示例,而不仅仅是训练数据的一个子集。
也有一些是在每个更新步骤中查看较小的训练数据子集
视频中使用批量梯度下降进行线性回归