Tensorflow2.x版本常用函数

TensorFlow2.x中的常用函数

合并与分割

tf.concat()在特定的维度上进行合并

tf.concat(tensor, axis)
其中 tensors 保存了所有需要合并的张量 List，axis 指定需要合并的维度。

a = tf.random.normal([4,35,8]) 
b = tf.random.normal([6,35,4])
tf.concat([a,b], axis = 0)

Output:

tf.stack()

tf.stack(tensors, axis)
是一个堆叠类型的合并，在新的维度上进行合并
其中 tensors 保存了所有需要合并的张量 List，axis >= 0时，在axis之前插入维度；axis<0时，在axis的后方插入维度。

a = tf.random.normal([35,8])
b = tf.random.normal([35,8])
tf.stack([a,b],axis=0) 
tf.stack([a,b], axis = -1)

Output:

tf.split()

合并操作的逆过程就是分割，将一个张量分拆为多个张量。
通过 tf.split(x, axis, num_or_size_splits)可以完成张量的分割操作，其中
❑ x：待分割张量
❑ axis：分割的维度索引号 ❑ num_or_size_splits：切割方案。当num_or_size_splits 为单个数值时，如 10，表示切割为 10 份；当 num_or_size_splits 为 List 时，每个元素表示每份的长度，如[2,4,2,2]表示
切割为 4 份，每份的长度分别为 2,4,2,2

x = tf.random.normal([10,35,8])
# 等长切割
result = tf.split(x,axis=0,num_or_size_splits=10)
len(result)
Output: 10

# 自定义长度的切割
result = tf.split(x,axis=0,num_or_size_splits=[4,2,2,2])
len(result)
Output: 4

数据计算

向量范数(Vector norm)是表征向量“长度”的一种度量方法，在神经网络中，常用来
表示张量的权值大小，梯度大小等。常用的向量范数有：
❑ L1 范数，定义为向量的所有元素绝对值之和
‖‖1 = ∑||

❑ L2 范数，定义为向量的所有元素的平方和，再开根号
‖‖2 = √∑||2

❑ ∞ −范数，定义为向量的所有元素绝对值的最大值：
‖‖∞ = (||)
对于矩阵、张量，同样可以利用向量范数的计算公式，等价于将矩阵、张量拉平成向量后计算。

tf.norm()

In [13]: x = tf.ones([2,2])
tf.norm(x,ord=1) # 计算 L1 范数
Out[13]: 
In [14]: tf.norm(x,ord=2) # 计算 L2 范数
Out[14]: 
In [15]: import numpy as np
tf.norm(x,ord=np.inf) # 计算∞范数
Out[15]: 

数值复制、填充与限制

对于图片数据的高和宽、序列信号的长度，维度长度可能各不相同。为了方便网络的并行计算，需要将不同长度的数据扩张为相同长度，之前我们介绍了通过复制的方式可以增加数据的长度，但是重复复制数据会破坏原有的数据结构，并不适合于此处。通常的做法是，在需要补充长度的信号开始或结束处填充足够数量的特定数值，如 0，使得填充后的长度满足系统要求。那么这种操作就叫做填充(Padding)。
填充操作可以通过 tf.pad(x, paddings)函数实现，paddings 是包含了多个
[ , ℎ ]的嵌套方案 List，如[[0,0],[2,1],[1,2]]表示第一个维度不填充，第二个维度左边(起始处)填充两个单元，右边(结束处)填充一个单元，第三个维度左边填充一个单元，右边填充两个单元。考虑上述 2 个句子的例子，需要在第二个句子的第一个维度的右边填充 2 个单元，则 paddings 方案为[[0,2]]：

tf.pad()

a = tf.constant([1,2,3,4,5,6])
b = tf.constant([7,8,1,6])
b = tf.pad(b, [[0,2]]) # 填充b

Output:

#填充后句子张量形状一致，再将这 2 句子 Stack 在一起：
tf.stack([a,b],axis=0) # 合并

Output:

tf.tile()

通过 tf.tile 函数可以在任意维度将数据重复复制多份，如 shape 为[4,32,32,3]的数据，复制方案 multiples=[2,3,3,1]，即通道数据不复制，高宽方向分别复制 2 份，图片数再复制1 份:

x = tf.random.normal([4,32,32,3])
tf.tile(x,[2,3,3,1]) # 数据复制

tf.maximum() tf.minimum()

在 TensorFlow 中，可以通过 tf.maximum(x, a)实现数据的下限幅： ∈ [, +∞)；可以通过 tf.minimum(x, a)实现数据的上限幅： ∈ (−∞,]：

x = tf.range(9)
tf.maximum(x,2) # 下限幅 2



tf.minimum(x,7) # 上限幅 7

tf.clip_by_value()

tf.clip_by_value(tensor, 下限，上限)

x = tf.range(9)
tf.clip_by_value(x,2,7) # 限幅为 2~7

其他高级操作

tf.gather()

tf.gather(tensor, num, axis)
num为想要收集数据的索引号
axis是按照哪个维度来进行检索

x = tf.random.uniform([4,35,8],maxval=100,dtype=tf.int32)
tf.gather(x,[0,1],axis=0) # 在班级维度收集第 1-2 号班级成绩册

tf.gather_nd()用法与tf.gather()类似，用于根据多维的坐标来检索数据

tf.boolean_mask()

tf.boolean_mask(x,mask=[True, False,False,True],axis=0)
mask是掩码，该方法根据掩码来进行维度的检索

tf.boolean_mask(x,mask=[True, False,False,True],axis=0)  x = [4, 35, 8]
Out[49]:

tf.where()

通过 tf.where(cond, a, b)操作可以根据 cond 条件的真假从 a 或 b 中读取数据，条件判定规则如下：
= { 为 为
其中 i 为张量的索引，返回张量大小与 a,b 张量一致，当对应位置中为 True，位置从中复制数据；当对应位置中为 False，位置从中复制数据。考虑从 2 个全 1、 全 0 的 3x3 大小的张量 a,b 中提取数据，其中cond 为 True 的位置从 a 中对应位置提取，cond 为 False 的位置从 b 对应位置提取：

In [53]:
a = tf.ones([3,3]) # 构造 a 为全 1
b = tf.zeros([3,3]) # 构造 b 为全 0
# 构造采样条件
cond = tf.constant([[True,False,False],[False,True,False],[True,True,False]])
tf.where(cond,a,b) # 根据条件从 a,b 中采样
Out[53]:

通过对于cond的where操作会得到true元素所在的位置

In [55]:tf.where(cond) # 获取 cond 中为 True 的元素索引

Out[55]:

tf.meshgrid()

通过 tf.meshgrid 可以方便地生成二维网格采样点坐标，方便可视化等应用场合。考虑2 个自变量 x,y 的 Sinc 函数表达式为：
=(2 + 2) 2 + 2
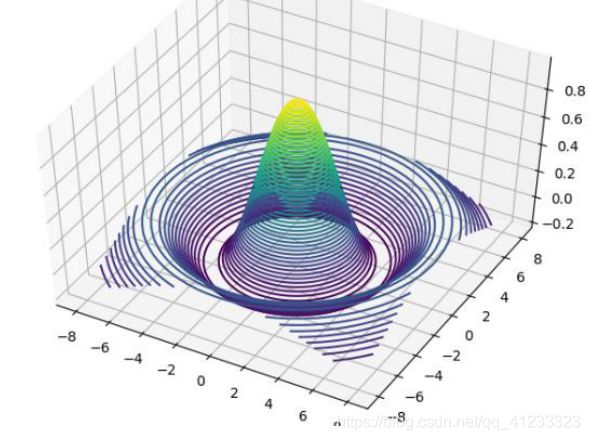
如果需要绘制函数在 ∈ [−8,8], ∈ [−8,8]区间的 Sinc 函数的 3D 曲面，如图 所示，则首先需要生成 x,y 的网格点坐标{(, )}，这样才能通过 Sinc 函数的表达式计算函数在每个(, )位置的输出值 z。可以通过如下方式生成 1 万个坐标采样点：

points = []
for x in range(-8,8,100): # 循环生成 x 坐标
	for y in range(-8,8,100): # 循环生成 y 坐标
		z = sinc(x,y) # 计算 sinc 函数值
		points.append([x,y,z]) # 保存采样点

很明显这种方式串行计算效率极低，那么有没有简洁高效地方式生成网格坐标呢？答案是肯定的，tf.meshgrid 函数即可实现。
通过在 x 轴上进行采样 100 个数据点，y 轴上采样 100 个数据点，然后通过
tf.meshgrid(x, y)即可返回这 10000 个数据点的张量数据，shape 为[100,100,2]。为了方便计算，tf.meshgrid 会返回在 axis=2 维度切割后的 2 个张量 a,b，其中张量 a 包含了所有点的 x坐标，b 包含了所有点的 y 坐标，shape 都为[100,100]：

x = tf.linspace(-8.,8,100) # 设置 x 坐标的间隔
y = tf.linspace(-8.,8,100) # 设置 y 坐标的间隔
x,y = tf.meshgrid(x,y) # 生成网格点，并拆分后返回
x.shape,y.shape # 打印拆分后的所有点的 x,y 坐标张量 shape

Output：(TensorShape([100, 100]), TensorShape([100, 100]))

Sinc 函数在 TensorFlow 中实现如下：

z = tf.sqrt(x**2+y**2) 
z = tf.sin(z)/z # sinc 函数实现

通过 matplotlib 即可绘制出函数在 ∈ [−8,8], ∈ [−8,8]区间的 3D 曲面

fig = plt.figure()
ax = Axes3D(fig)

根据网格点绘制 sinc 函数 3D 曲面

ax.contour3D(x.numpy(), y.numpy(), z.numpy(), 50)
plt.show()

注：.numpy()方法只用在使用tf.enable_eager_execution()(命令式编程开启)后才有的方法, 否则会有==AttributeError: ‘Tensor’ object has no attribute ‘numpy’==报错