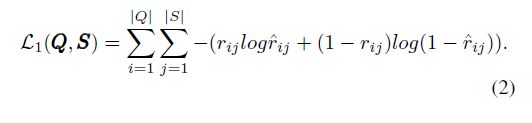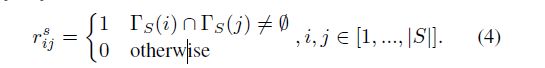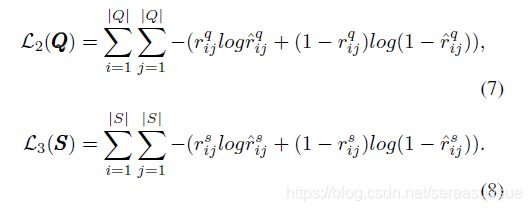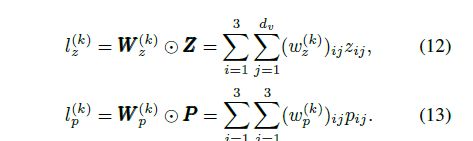Improving Knowledge Tracing via Pre-training Question Embeddings
Improving Knowledge Tracing via Pre-training Question Embeddings
论文：Improving Knowledge Tracing via Pre-training Question Embeddings | IJCAI
代码：https://github.com/lyf-1/PEBG
人工智能大会 IJCAI
摘要
知识追踪(KT)定义的任务是根据学生的历史反应预测学生是否能正确回答问题。尽管许多研究致力于开发问题信息，但问题和技能中丰富的高级信息没有被很好地提取出来，使得先前的工作难以充分执行。在本文中，我们证明了通过在丰富的边信息上对每个问题进行预训练嵌入，然后在所获得的嵌入上训练深度KT模型，可以在KT上实现大的增益。具体来说，边信息包括问题难度和包含在问题和技能之间的二分图中的三种关系。为了预训练问题嵌入，我们建议使用基于产品的神经网络来恢复边信息。因此，在现有深度KT模型中采用预包含嵌入，在三个常见的KT数据集上显著优于最先进的基线。
背景
虽然已有发深度的KT模型很好地预测学生的技能水平，但是存在一个主要的限制，即没有考虑特定问题的信息
具有相同技能的问题可能会有不同的难度，因此技能水平预测不能准确反映学生对特定问题的知识状态。虽然利用特定问题的信息在更细粒度的层次上解决KT是非常必要的，但是存在一个主要问题，即学生和问题之间的交互极其稀疏，如果直接使用问题作为网络输入，将导致灾难性的失误
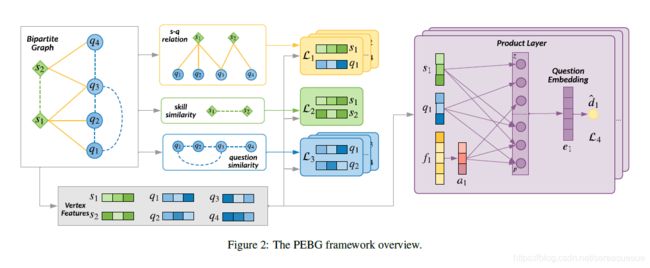
本文提出了一种预训练方法，称为二分图预训练嵌入法(PEBG)，利用所有有用的边信息学习每个问题的低维嵌入。具体来说，辅助信息包括问题难度以及三种关系:显性问题技能关系、隐性问题相似性和技能相似性。为了有效地提取边信息中包含的知识，我们采用产品层融合问题顶点特征、技能顶点特征和属性特征来产生最终的问题嵌入。这样，学习的问题嵌入将保留问题难度信息以及问题和技能之间的关系。
本文的贡献总结如下。
- 第一个使用问题技能关系的二分图来获得问题嵌入的，它提供了丰富的关系信息。
- 我们提出了一种称为PEBG的预训练方法，它引入了一个产品层来融合所有的输入特征，以获得最终的问题嵌入。
- PEBG得到的问题嵌入可以整合到现有的深度KT模型中。在三个真实数据集上的实验结果表明，使用PEBG可以优于最先进的模型，平均提高AUC 8.6%
问题表示
表示学生的过去学习交互
让
成为所有不同问题的集合，让
成为所有不同技能的集合。通常一个技能包含很多问题，一个问题和几个技能有关。所以问题-技能关系自然可以表示为二部图G = (Q，S，R)，其中R =[rij]∞{ 0，1}|Q|×|S|是二元邻接矩阵。如果问题qi和技能sj之间有边，那么rij = 1；否则rij = 0.这里我们介绍我们将用来训练模型中嵌入的信息，包括图中的信息和难度信息。
定义1(明确的问题-技能关系)。给定问题技能二部图，技能顶点和问题顶点之间的关系是显式问题技能关系，即问题顶点I和技能顶点j之间的显式关系取决于rij是否=1。
定义2(隐性问题相似性和技能相似性)。给定问题技能二部图，两个具有公共邻居问题顶点的技能顶点之间的关系被定义为技能相似性。同样，问题相似性是指共享共同邻居技能顶点的两个问题顶点之间的关系。
定义3(问题难度)。一个问题qi的问题难度di被定义为从训练数据集计算的正确回答的比率。所有的题难点形成一个向量d = [di] ∈ R|Q|。
模型
输入特征
为了预先训练问题嵌入，我们使用了如下三种特征。需要注意的是，顶点特征是随机初始化的，将在预处理阶段进行更新，这相当于学习从一次编码到连续特征的线性映射。
技能顶点特征：由特征矩阵
表示，其中dv是特征的维数。对于一个技能si，顶点特征表示为si，是矩阵s的第I行。
问题顶点特征用特征矩阵
表示，特征矩阵与技能顶点特征具有相同的维数dv。对于一个问题qj，顶点特征表示为qj，是矩阵q的第j行。
属性特征:是与问题难度相关的特征，如平均反应时间、问题类型等。对于问题
，我们将特征连接为是特征的数量![f{_{i}}=[f{_{i1}};\cdots;f{_{m}} ]](http://img.e-com-net.com/image/info8/909b197c43fb466a8218378d167c5960.gif){kind=small}
。如果第j个特征是分类的(例如，。问题类型)。如果第j个特征是数字的(例如,平均响应时间)。
二部图约束
技能和问题顶点特征通过二分图约束进行更新。由于图中存在不同的关系，我们设计了不同类型的约束，以便顶点特征可以保留这些关系。
显性问题-技能关系
在问题技能二部图中，问题顶点和技能顶点之间存在边，这是一个明确的信号。类似于LINE中的一阶近似模型[唐等，。2015]中，我们通过考虑技能和问题顶点之间的局部邻近性来建模显式关系。具体来说，我们使用内积来估计嵌入空间中问题和技能顶点之间的局部接近度，
其中σ(x)是sigmoid函数，它将关系值转换为概率。
为了保持显式关系，通过交叉熵损失函数，局部邻近性被强制接近二分图中的技能问题关系:
隐含的相似性
PEBG中使用的隐含相似性表示二分图中邻域之间的相似性。具体来说，存在两种相似性:技能相似性和问题相似性。我们希望使用隐含的相似性来同时更新顶点特征
难度约束
问题的难度信息在KT预测中很重要，但是它不包含在二分图中。因此，我们希望最终的问题嵌入能够恢复难度信息。[Vie和Kashima，2019]使用因式分解机器[Rendle，2010]对边信息进行编码，探索学生建模的特征交互。在本文中，我们使用属性特征与顶点特征的交互来学习高质量的嵌入。特别是受[屈等，。2016]，产品层用于学习高阶特征交互。
对于一个问题q(为了清楚起见省略了它的下标)，我们有它的问题顶点特征q和它的属性特征f。为了通过产品层使属性特征与顶点特征相互作用，我们首先使用由wa参数化的线性层将属性特征f映射到低维特征表示，该低维特征表示被表示为
。假设与
q相关的技能集合，我们使用C中所有技能顶点特征的平均表示作为q的相关技能特征，表示为s,数学上
我们使用顶点特征q、平均技能特征s0和属性特征a来生成问题q的线性信息Z和二次信息P。具体来说，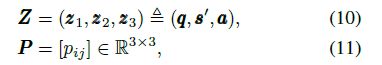
然后我们引入一个乘积层，它可以将这两个信息矩阵转换成信号向量lz和lp，如图2所示。转换方程如下
……
实验
在这一部分，我们通过实验来评估基于问题嵌入的知识追踪模型的性能。
数据集
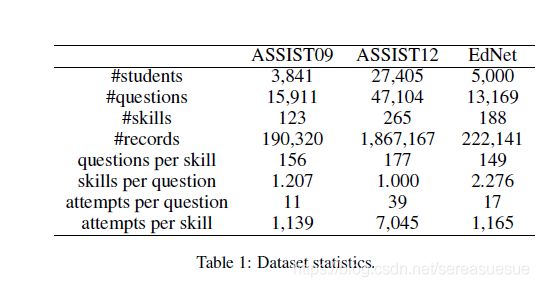
我们使用三个真实世界的数据集，这三个数据集的统计数据如表1所示
ASSIST09和ASSIST12都来自助教在线辅导平台[冯等人。2009]. 对于这两个数据集，我们在没有技能和支架问题的情况下移除记录。我们还删除少于三条记录的用户。经过预处理，ASSIST09数据集由123项技能、3841名学生回答的15911个问题组成，总共有190320条记录。ASSIST12数据集包含265项技能，27，405名学生回答了47，104个问题，记录为1，867，167条。
EdNet是由[Choi等人。2019]. 在本实验中，我们使用了由学生问题解决日志组成的EdNet-KT1数据集，并随机抽取了5000名学生的222，141条记录，其中包含13，169个问题和188项技能。
-
- 比较模型
为了说明我们的模型的有效性，并展示我们的模型对现有深度KT模型的改进，我们比较了最先进的深度KT模型之间的预测性能。我们将比较模型分为技能级模型和问题级模型。
技能水平模型
技能水平模型只使用技能嵌入作为输入，它们都跟踪学生对技能的掌握。
- BKT [Corbett and Anderson，1994]是一个二态动态贝叶斯网络，由初始知识、学习率、滑动和猜测参数定义。
- DKT[皮赫等人。2015]使用递归神经网络对学生技能学习进行建模。
- DKVMN[张等。2017]使用键值存储网络来存储技能的基本概念表示和状态。
问题级模型
除了技能级模型，以下模型利用问题信息进行问题级预测。
- KTM [Vie and Kashima，2019]利用因式分解机器进行预测，让学生id、技能id、问题特征相互作用。
- DKT-Q是我们对DKT模型的扩展，该模型直接使用问题作为DKT的输入，并预测学生对每个问题的反应。
- dkwmn-Q是我们对dkwmn模型的扩展，直接使用问题作为dkwmn的输入，预测学生对每个问题的反应。
- DHKT是DKT的扩展模型，它模拟技能-问题关系，还可以预测学生对每个问题的反应。
我们基于技能级深度学习模型来测试我们的模型。PEBG+DKT和PEBG+dkwmn利用PEBG预先训练的问题嵌入，使DKT和dkwmn实现问题级预测。
实施细节
为了评估每个数据集的性能，我们使用曲线下面积作为评估指标。
PEBG只有几个超参数。顶点特征dv的尺寸设置为64.最后一个问题嵌入维数d = 128.方程中的λ。(17)为0.5.我们使用亚当算法来优化我们的模型，三个数据集的小批量设置为256，学习率为0.001.我们还使用概率为0.5的辍学来减轻过度适应。我们将每个数据集分为80%用于训练和验证，20%用于测试。对于每个数据集，训练过程重复五次，我们报告平均测试AUC。
对于ASSIST09和ASSIST12数据集，平均响应时间和问题类型用作属性特征。对于EdNet数据集，平均响应时间被用作属性特征。
性能预测
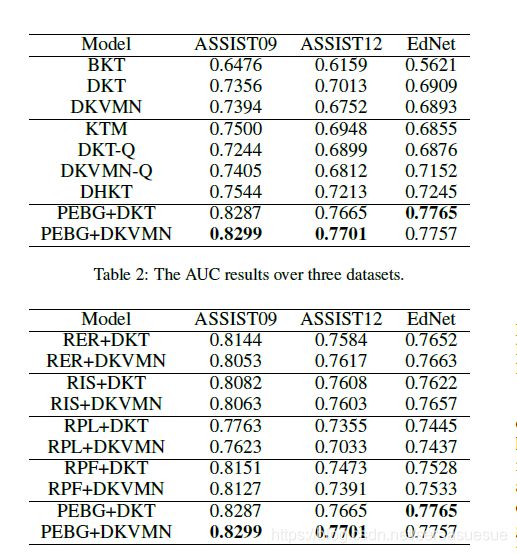
表2说明了所有比较模型的预测性能，我们发现如下几个观察结果。
所提出的PEBG+DKT和PEBG+DKVMN模型在所有三个数据集上都获得了最高的AUC。特别是在ASSIST09数据集上，我们的PEBG+DKT和PEBG+DKVMN型号的AUC为0.8287，并且0.8299，与DKT和德国KVMN实现的0.7356和0.7394相比，平均显著提高了9.18%。在ASSIST12数据集上，结果显示平均增加了8%，PEBG+DKT的AUC为0.7665，PEBG+dkwmn的AUC为0.7701，而DKT的AUC为0.7013，dkwmn为0.6752。在EdNet数据集上，PEBG+DKT和PEBG+dkwmn比最初的DKT和dkwmn平均提高了8.6%。
在所有比较的模型中，BKT的表现最差。DKT、德国KVMN和KTM的表现相似。通过比较DKT和DKT-Q、dkwmn和dkwmn-Q的性能，我们发现DKT-Q和dkwmn-Q没有表现出优势，这表明直接将现有的深度KT模型应用于问题级预测会遇到问题交互稀疏问题。还有我们的PEBG、即使在稀疏数据集上，模型也能很好地改善DKT和DKVMN。尽管DHKT的表现优于DKT，但它的表现仍然不如我们提出的模型，这说明了PEBG在利用技能和问题之间更复杂的关系方面的有效性。
消融研究
在这一部分，我们进行了一些消融研究，以调查我们提出的模型的三个重要组成部分的有效性:(1)显式关系；(2)隐性相似性；(3)产品层。我们设置了四个比较设置，它们的性能如表3所示.下面列出了四种设置的详细信息:
- RER(删除显式关系)不考虑问题和技能之间的显式关系，即。从方程中移除L1。(17).
- RIS(消除隐含相似性)不考虑问题和技能之间的隐含相似性，即。从方程中删除L2和L3。(17).
- RPL(移除产品层)直接连接q、s0和a作为预训练的问题嵌入，而不是使用产品层。
- RPF(用全连接层替换产品层)将q、s0和a连接起来作为全连接层而不是产品层的输入。
除了上面提到的变化，模型的其他部分和实验设置保持不变。
从表3中我们可以发现(1) PEBG+DKT和PEBG+dkwmn表现最好，表明了模型不同组成部分的功效。(2)当去除显性关系和隐性相似性时，模型显示出相似的下降程度，这意味着这两条信息同等重要。(3)去掉产品层对性能伤害很大，使用全连接层也有较低的性能。通过探索
在特征交互方面，与直接连接特征相比，产品层有望学习高阶潜在模式。(4)在没有乘积层的情况下，RPF和RPL是标准的图嵌入方法，它们使用二分图的一阶和二阶邻居信息。并且我们提出的预训练模型PEBG可以更好地提高现有深度KT模型的性能。
嵌入比较
我们使用t-SNE [Maaten和Hinton，2008]将PEBG预先训练的多维问题嵌入和其他问题级深度KT模型学习的问题嵌入投射到二维点。
图3显示了问题嵌入的可视化。DKT和DKVMN学习的问题嵌入是随机混合的，完全失去了问题和技能之间的联系。DHKT学习的不同技能的问题嵌入是完全分离的，未能捕捉到隐含的相似性.由PEBG预先训练的问题嵌入结构良好。同一技能中的题型彼此接近，与共同技能无关的题型分开很好。PEBG+DKT和PEBG+dkwmn对PEBG预处理的问题嵌入进行微调，使其更适合KT任务，同时保留问题和技能之间的关系。
结论
本文提出了一种新的预训练模型PEBG，该模型首先将问题-技能关系表示为一个二分图，并引入一个产品层来学习用于知识追踪的低维问题嵌入。在真实数据集上的实验表明，PEBG显著提高了现有深度KT模型的性能。此外，可视化研究显示了PEBG在捕获问题嵌入方面的有效性，为其高性能提供了直观的解释。