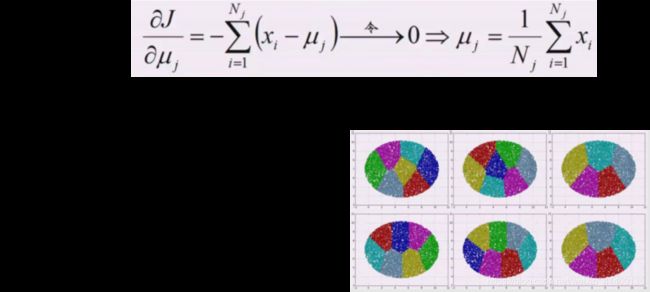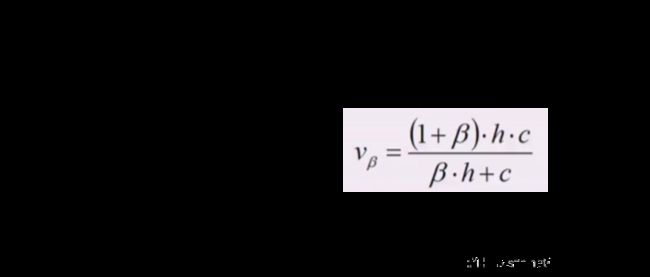机器学习————聚类

机器学习————聚类

聚类

聚类是一个无监督的算法

有X
没有Y
利用X相似性
对大量未标注的数据集，按内在相似性划分为多个类别，类别内相似度大，类之间相似度小

聚类算法

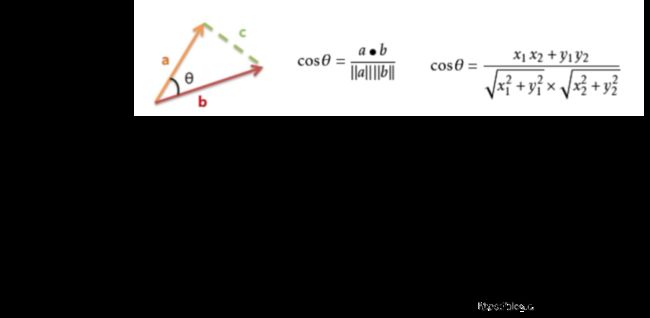
计算距离

欧几里得距离（欧式距离）

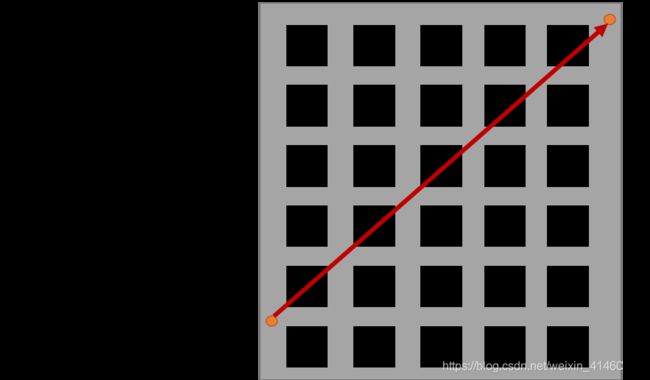
欧几里得距离（欧式距离）
曼哈顿距离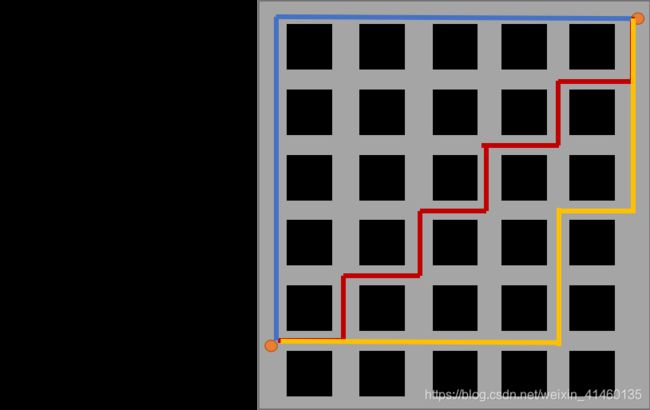
闵可夫斯基距离

闵氏距离不是一种距离，而是一组距离的定义，其中的p是一个参数

当p=1时，就是曼哈顿距离
当p=2时，就是欧式距离
当p->∞时，就是切比雪夫距离

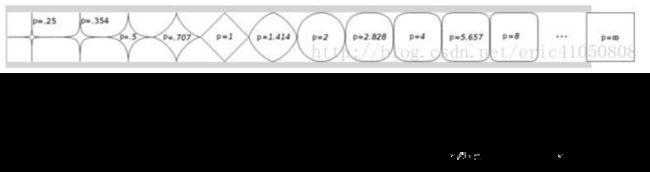
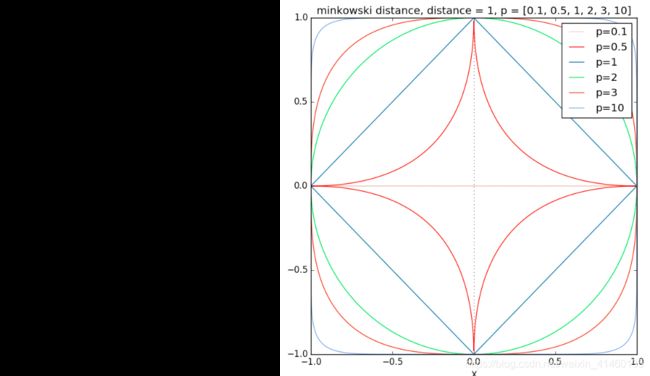
相似度

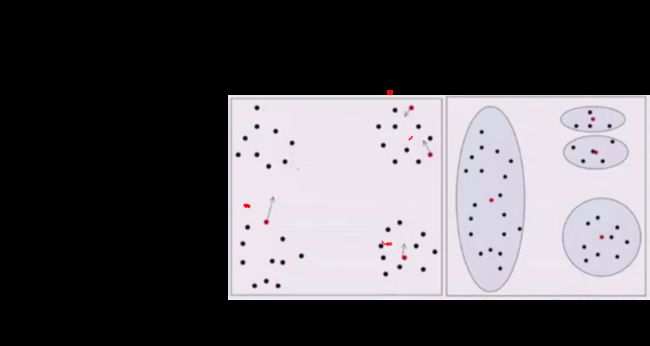
簇

聚类试图将数据中的样本划分为若干个通常是不相交的子集，每个子集称为一个“簇”(cluster)

本质上，N个样本，映射到K个簇中
每个簇至少有一个样本
一般情况下，一个样本只属于一个簇(也有一个样样本属于多个簇的)

最基本：
先给定一个初始划分，迭代改变样本和簇的隶属关系，每次都比前一次好

K-Means聚类

聚类是一种无监督的机器学习任务，它可以自动将数据划分成类cluster。因此聚类分组不需要提前被告知所划分的组应该是什么样子的。因为我们甚至可能都不知道我们再寻找什么，所以聚类是用于知识发现而不是预测

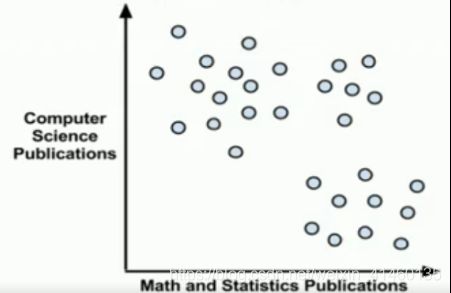
聚类原则是一个组内的记录彼此必须非常相似，而与该组之外的记录截然不同。所有聚类做的就是遍历所有数据，然后找到这些相似性。

使用距离来分配和更新类。


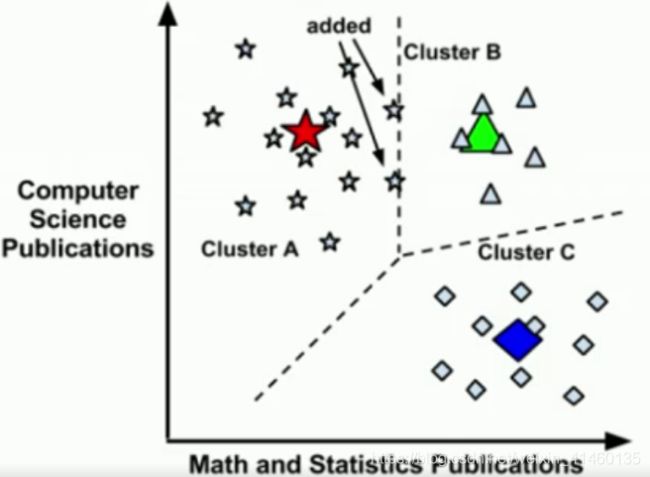
选择K个初始的簇中心，随机的（拍脑袋给的），或者先验知识给的
某一个样本和某一个聚类中心的距离
计算所属聚类的样本均值

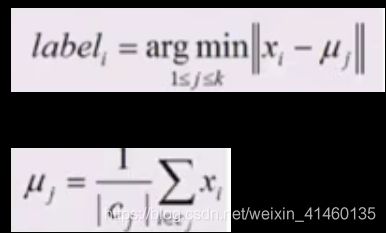
K-Means实现

# encoding: utf-8

import numpy as np
import matplotlib.pyplot as plt
import sklearn.datasets as ds
import matplotlib.colors
from sklearn.cluster import KMeans

def expand(a, b):
    """
    为了扩展x，y轴的长度
    """
    d = (b - a) * 0.1
    return a-d, b+d

if __name__ == '__main__':
    # 创建400个样本
    N = 400
    # 准备分出4个类别
    centers = 4
    # 创建聚类的数据（按照4个正太分布创建点）【想看看方差一样的，数据量一样的，分类效果好不好】
    data, y = ds.make_blobs(N, n_features=2, centers=centers, random_state=2)
    # print(data)
    # 方差和上面不一样，方差越大，数据集越分散；方差越小，数据集越密集【想看看方差不一样，数据量一样，分类效果好不好】
    data2, y2 = ds.make_blobs(N, n_features=2, centers=centers, cluster_std=(1, 2.5, 0.5, 2), random_state=2)
    # 从原来数据中选一部分的数据出来【想看看从每条数据里选不同的样本数量的分类效果好不好】
    data3 = np.vstack((data[y==0][:], data[y==1][:50], data[y==2][:20], data[y==3][:5]))
    # 按道理来说，聚类是不需要y值的，这里的y主要是为了看我们的聚类效果准不准
    y3 = np.array([0] * 100 + [1] * 50 + [2] * 20 + [3] * 5)
    # print(y3)

    # k-means++是为了改变初始化的值，所以参数名称是init
    cls = KMeans(n_clusters=5, init='k-means++')
    y_hat = cls.fit_predict(data)
    y2_hat = cls.fit_predict(data2)
    y3_hat = cls.fit_predict(data3)

    # matplotlib.rcParams['font.sans-serif'] = [u'SimHei']
    cm = matplotlib.colors.ListedColormap(list('rgbm'))

    plt.figure(figsize=(9, 10), facecolor='w')
    # subplot用来画子表的 4行 2列 1第一个图
    plt.subplot(421)
    plt.title("Original Data")
    # scatter散点图
    plt.scatter(data[:, 0], data[:, 1], c=y, s=10, cmap=cm, edgecolors='none')
    x1_min, x2_min = np.min(data, axis=0)
    x1_max, x2_max = np.max(data, axis=0)

    x1_min, x1_max = expand(x1_min, x1_max)
    x2_min, x2_max = expand(x2_min, x2_max)

    plt.xlim(x1_min, x1_max)
    plt.ylim(x2_min, x2_max)
    plt.grid(True)

    plt.subplot(422)
    plt.title("KMeans ++ Clusting")
    plt.scatter(data[:, 0], data[:, 1], c=y_hat, s=30, cmap=cm, edgecolors='none')
    plt.xlim(x1_min, x1_max)
    plt.ylim(x2_min, x2_max)
    plt.grid(True)

    """
    对数据进行旋转
    """
    m = np.array(((1, 1), (1, 3)))
    data_r = data.dot(m)
    y_r_hat = cls.fit_predict(data_r)


    plt.subplot(423)
    plt.title('Rotation Data')
    plt.scatter(data_r[:, 0], data_r[:, 1], c=y, s=30, cmap=cm, edgecolors='none')
    x1_min, x2_min = np.min(data_r, axis=0)
    x1_max, x2_max = np.max(data_r, axis=0)

    x1_min, x1_max = expand(x1_min, x1_max)
    x2_min, x2_max = expand(x2_min, x2_max)

    plt.xlim(x1_min, x1_max)
    plt.ylim(x2_min, x2_max)
    plt.grid(True)

    plt.subplot(424)
    plt.title('Rotated KMeans++ Clusting')
    plt.scatter(data_r[:, 0], data_r[:, 1], c=y_r_hat, s=30, cmap=cm, edgecolors='none')
    plt.xlim(x1_min, x1_max)
    plt.ylim(x2_min, x2_max)
    plt.grid(True)


    plt.subplot(425)
    plt.title('Different Variance Data')
    plt.scatter(data2[:, 0], data2[:, 1], c=y2_hat, s=30, cmap=cm, edgecolors='none')
    x1_min, x2_min = np.min(data2, axis=0)
    x1_max, x2_max = np.max(data2, axis=0)

    x1_min, x1_max = expand(x1_min, x1_max)
    x2_min, x2_max = expand(x2_min, x2_max)

    plt.xlim(x1_min, x1_max)
    plt.ylim(x2_min, x2_max)
    plt.grid(True)

    plt.subplot(426)
    plt.title('Different Variance Data KMeans++ Clusting')
    plt.scatter(data2[:, 0], data2[:, 1], c=y2_hat, s=30, cmap=cm, edgecolors='none')
    plt.xlim(x1_min, x1_max)
    plt.ylim(x2_min, x2_max)
    plt.grid(True)

    plt.tight_layout(2, rect=(0, 0, 1, 0.97))
    plt.show()

K-Means 改进

K-Mediods

数组1,2,3,4,100的均值为22， 其实求均值的话，离里面大多数的值还是比较远的

取中位数的话是3， 更好一些， 因为100可能是噪声

二分K-Means

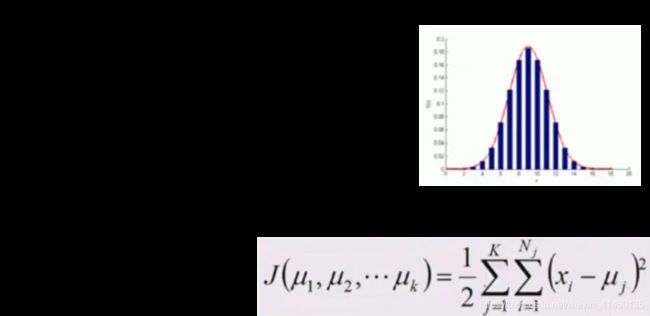
K均值损失函数

K = N, MSE 为 0

K = 1, MSE就是原始数据的方差

选择一开始下降速度快，后来下降速度慢的

elbow method， 不止于K均值

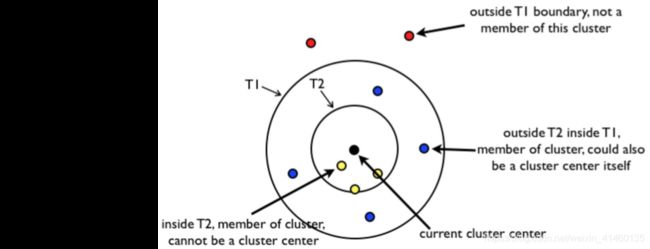
Canopy聚类

聚类的评估

层次聚类

理解起来有点像无监督的决策树

分裂的层次聚类： DIANA

把原始数据集去不断的分裂，然后去计算每个子数据集里面的相似性，然后不断的分裂，把数据集分为很多的类别

凝聚的层次聚类： AGNES

把一个个样本，不断的自底向上的聚类，然后一层一层的来聚，最后聚成一个完整的数据集，这种用的更多一些

如果我们只关心结果的话，那么在某一时刻是要停止聚类的，在一些数据集中做层次聚类是合适的，包含层次的数据集！ 地域！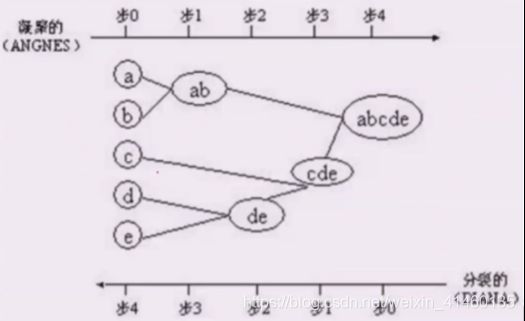
如果两个样本，可以很好的度量距离，如果已经聚了一层，如何度量簇之间的相似性

最小距离：两个簇中，最接近样本的距离，城市和城市边界最短距离，成链状一条直线了

最大距离：两个簇中，最远的样本的距离，某一个簇存在异常值就很麻烦，簇本身比较狭长

平均距离：

两两样本距离的平均

两两样本距离的平方和

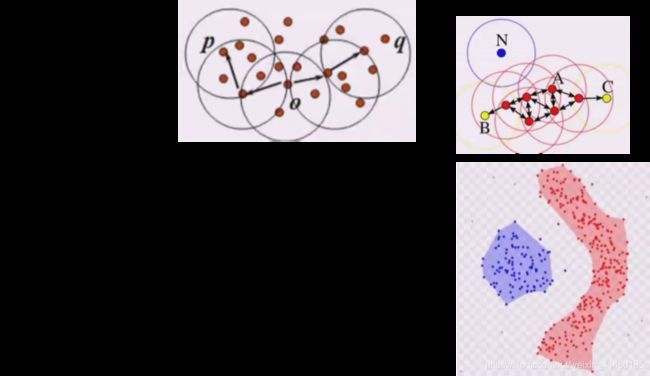
密度聚类

统计样本周边的密度，把密度给定一个阈值，不断的把样本添加到最近的簇

人口密度，根据密度，聚类出城市

解决类似圆形的K-Means聚类的缺点，密度聚类缺点计算复杂度大，空间索引来降低计算时间，降低查找速度

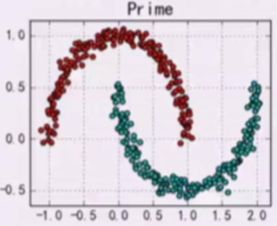
DBSCAN

DBSCAN实现

import numpy as np
import matplotlib.pyplot as plt
import sklearn.datasets as ds
import matplotlib.colors
from sklearn.cluster import DBSCAN
from sklearn.preprocessing import StandardScaler


def expand(a, b):
    d = (b - a) * 0.1
    return a-d, b+d

if __name__ == '__main__':
    N = 1000
    centers = [[1, 2], [-1, -1], [1, -1], [-1, 1]]
    # make_blobs模拟生成聚类的数据 centers：给定的中心点，根据中心点模拟生成数据 cluster_std生成数据的方差
    data, y = ds.make_blobs(N, n_features=2, centers=centers, cluster_std=[0.5, 0.25, 0.7, 0.5], random_state=0)
    # StandardScaler 做归一化的：先做均值归一化，再说方差归一化
    data = StandardScaler().fit_transform(data)
    # 数据的参数 (epsilon, min_sample)第一个是r，第二个是阈值
    params = ((0.4, 5), (0.4, 10), (0.3, 15), (0.5, 5), (0.2, 10), (0.6, 15))

    plt.figure(figsize=(12, 8), facecolor='w')
    # plt.suptitle('DBSCAN Clusting', fontsize=20)

    for i in range(6):
        eps, min_samples = params[i]
        model = DBSCAN(eps=eps, min_samples=min_samples)
        model.fit(data)
        y_hat = model.labels_
        # print(y_hat)
        core_indices = np.zeros_like(y_hat, dtype=bool)

        core_indices[model.core_sample_indices_] = True
        # print(core_indices)
        y_unique = np.unique(y_hat)
        # print(y_hat)
        # 假设有离群点 n_cluster - 1
        n_clusters = y_unique.size - (1 if -1 in y_hat else 0)
        print(y_unique, "聚类簇的个数为：", n_clusters)

        plt.subplot(2, 3, i+1)
        # 谱： 提取更好的特征（特征提取的作用）
        clrs = plt.cm.Spectral(np.linspace(0, 0.8, y_unique.size))
        # print(clrs)
        for k, clr in zip(y_unique, clrs):
            cur = (y_hat == k)
            if k == -1:
                plt.scatter(data[cur, 0], data[cur, 1], s=20)
                continue
            # 把我们分类好的类别，一个点一个点画出来（画离群点）
            plt.scatter(data[cur, 0], data[cur, 1], s=30, c=clr, edgecolors='k')
            # 把我们分类好的类别，一个点一个点画出来（画非离群点）
            plt.scatter(data[cur & core_indices][:, 0], data[cur & core_indices][:, 1], s=60, c=clr, marker='o', edgecolors='k')
        x1_min, x2_min = np.min(data, axis=0)
        x1_max, x2_max = np.max(data, axis=0)
        x1_min, x1_max = expand(x1_min, x1_max)
        x2_min, x2_max = expand(x2_min, x2_max)
        plt.xlim((x1_min, x1_max))
        plt.ylim((x2_min, x2_max))
        plt.grid(True)
        plt.title(u'epsilon = %.1f  m = %d CA:%d' % (eps, min_samples, n_clusters), fontsize=16)


    plt.tight_layout()
    plt.subplots_adjust(top=0.9)
    plt.show()

密度可达

总结

聚类 无监督机器学习
（1）K-Means
把数据按照他自己本身的特性分为K类
K-Means++ 对初始点的选取进行了增强，首先随机选一个点，然后在选第二个点的时候，离前一个点越
近，概率越低
（2）密度聚类
我们通过测量两个点之间的密度（这个点周围在一定的范围内，有多少个点），来确定他们是不是在一
类