现代密码学 | 01：概述

现代密码学_电子科技大学_中国大学MOOC(慕课)
计算机网络安全原理_吴礼发、洪征编著_电子工业出版社出版_ISBN:9787121387272
现代密码学_杨波_清华大学出版社_ISBN:9787302465553

秋风阁——北溪入江流：https://focus-wind.com/
秋风阁——现代密码学 | 01：概述

密码学的基本概念

信息安全与安全威胁

现在我们处于信息时代，信息时代网络无处不在，网络给我们的学习生活工作提供了较大的便利。但与此同时，网络中面对的攻击也是无处不在的，互联网的快速发展，极大的威胁到了我们的信息安全。

威胁信息安全的因素

1. 环境和灾害因素
   1. 网络设备所处环境的温度、湿度、供电、静电、灰尘、电磁场等。
   2. 自然灾害中的水灾、火灾、地震、雷电等。
   3. 针对这些非人为因素已有较好的应对策略。
2. 人为因素
   1. 有意：人为主动的恶意攻击、违纪、违法和犯罪行为等。
   2. 无意：工作疏忽造成的失误（配置不当，弱口令）。
   3. 网络安全防护技术主要针对此类网络安全进行防护。
3. 系统自身因素
   1. 计算机硬件系统故障。
   2. 计算机软件故障或安全缺陷，包括系统软件（如操作系统）、支撑软件（如数据库管理系统）和应用软件的故障和缺陷。
   3. 网络和通信协议自身的缺陷。
   4. 系统自身的脆弱和不足（或称为“安全漏洞”）是造成信息系统安全问题的内部根源。

攻击手段分类

按发起攻击来源分类

1. 外部攻击：攻击者来自网络或计算机系统外部。
2. 内部攻击：指有权使用计算机，但无权访问某些特定的数据、程序或资源的人企图越权使用系统资源的行为。
   1. 假冒着：盗用其他合法用户的身份和口令的人。
   2. 秘密使用者：有意逃避审计机制和存取控制的人员。
3. 行为滥用：指计算机系统资源的合法用户有意或无意地滥用他们的特权。

从攻击对被攻击对象的影响分类

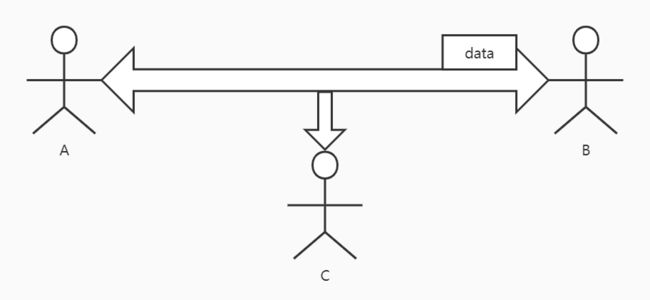
1. 被动攻击：通过窃听和监测来获取正在传输的信息，主要包括监听传输的报文内容和通信流量分析。
   1. 针对被动攻击的监测十分困难，对付被动攻击的重点不是检测，而是预防，可以通过加密来达到预防目的。
2. 主动攻击：包括对数据流的某些修改或者生成一个假的数据流。
   1. 主动攻击难以绝对地预防，但容易检测，所以重点在于检测并从破坏或造成的延迟中恢复过来。

密码学基本概念

密码学是网络安全的基础，很多网络安全的防护手段都是通过密码来实现的。

密码（cryptogram）

根据《中华人民共和国密码法》的定义：密码是指采用特定变换的方法对信息等进行加密保护、安全认证的技术、产品和服务。

密码学（cryptography）

• 密码学是研究编制密码和破译密码的技术科学。
  • 编码学：研究密码变化的客观规律，应用于编制密码以保护通信密码的。
  • 分析学（破译学）：应用于破译密码以获取通信情报的。
    如图所示，假设A和B在信道上进行数据通信，C为信道上的攻击者，意图获取或篡改双方的通信信息，针对这种简单的通信模型，所需的安全需求：

1. 机密性：有没有其他人看到通信数据
2. 完整性：通信数据是否被篡改
3. 消息源认证：这份数据是否是你发送的
4. 通信实体认证：这份数据是否是发给我的
5. 不可否认性：是否你真的给我发送过这份数据

密码系统、密码算法的基本模型

密码系统（Cryptosystem）通常也被称为密码体制。密码系统由五部分组成，以S表示密码系统，则可以描述为S = {M, C, K, E, D}，其中：

1. M（Messae）：明文空间。
   1. 明文：需要加密的信息。
2. C（Ciphertext）：密文空间。
   1. 密文：明文加密后的结果。
3. K（Key）：密钥空间。
   1. 密钥：进行加密和解密运输的关键。
   2. 加密密钥：加密运算使用的密钥。
   3. 解密密钥：解密运输使用的密钥。
4. E（Encryption）：加密算法。
   1. 加密：将明文变换为密文所使用的变换函数。
   2. C = E(k1, M)或C = E_k1(M)。
5. D（Decryption）：解密算法。
   1. 解密：将密文恢复为明文的变换函数。
   2. M = D(k2, C)或M = D_k2©。

密码算法的需求

• 密码算法需求
  • 可逆：算法的使用者可以将密文恢复成明文。
  • 不可逆：敌手无法将密文恢复成明文。
  • 密码参数：密钥
• 密码算法实际上是一个带有秘密参数的函数
  • 知道秘密参数，求逆非常容易。
  • 不知道秘密参数，求逆是不可行的。

密码算法分类

根据密钥分类

- 密码算法
	- 无密钥密码算法
		- 杂凑函数（Hash函数）
		- 单向置换
		- 随机序列
	- 对称密钥密码算法
		- 流密码
		- 分组密码
		- 消息摘要函数
	- 公钥（非对称）密码算法
		- 公钥加密
		- 数字签名
		- 身份认证

按照功能进行分类

• 机密性：
  • 对称密钥加密
    • 流密码
    • 分组密码
  • 公钥加密
• 完整性：
  • 杂凑函数（Hash函数）
  • 消息摘要函数
• 认证：
  • 数字签名
  • 身份认证协议
• 不可否认性：
  • 数字签名

对称密钥加密算法

对称密钥加密算法：指加密密钥和解密密钥相同或很容易相互推到出来。

• 特点：
  • 加解密密钥相同
  • 加解密速度块
• 应用：
  • 大量数据加密
  • 消息认证码
• 常见算法：
  • ZUC、DES、AES、SM4…

公开（非对称）密钥加密算法

公开（非对称）密钥加密算法：加解密密钥互不相同，从其一个密钥难以推导出另外一个密钥。公钥可公开，私钥不可随意泄露。

• 特点：
  • 加解密密钥不同
  • 加解密速度慢
• 应用：
  • 短消息加密
  • 数字签名
  • 身份认证
• 常见算法：
  • RSA、ECC、SM2、ELGamal…

杂凑函数（Hash函数）

针对任意长度的输入映射为定长输出，主要用于完整性验证。

• 特点：
  • 任意长输入映射为定长输出
  • 输入变换，输出发送不可预测的变化
  • 输出无法推导出输入
• 应用：
  • 完整性校验
• 常见算法：
  • SHA系列、MD5、SM3…

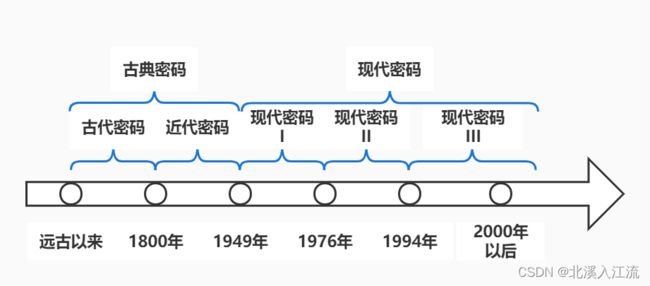
密码学发展简史

古典密码阶段

古代密码

特点

• 时间区域：从由人类以来到1800年
• 密码设计与分析被当作一门艺术
• 这一时期的密码学专家常常是凭直觉和信念来进行密码设计与分析，而不是靠推理证明
• 数据的保密基于加密算法的保密
• 密码工作者多为语言学家、猜谜高手等

著名密码算法

• 500 B.C.，古斯巴达“天书”密码（置换密码）
• 205-123 B.C.，古希腊人棋盘密码（代替密码）
• 50 B.C.，古罗马凯撒密码（代替密码）
• 16世纪，维吉尼亚密码（代替密码）

近代密码（密码机）

特点

• 时间区域：从1800到1949年
• 密码机的迅速发展
• 越来越多的数学家加入密码队伍

著名密码机

• 1795年，杰弗逊圆盘
• 1914年，美陆军和海军的M-138-T4
• 1918年，德国的Enigma密码机
• 1926年，Kryha密码机
• 1936年，瑞典的哈格林发明的Haglin密码机
• 美国TYPEX打字密码机

古典密码阶段

• 时间：
  • 1949年之前：古典密码
• 特点：
  • 密码学还不是科学，而是艺术
  • 出现一些密码算法和加密设备
  • 出现密码算法设计的基本手段（代替法、置换法）
• 保密性
  • 数据的保密基于加密算法的保密
• 里程碑事件
  • 1883年Kerckhoffs第一次明确提出了密码编码的原则：
    • 加密算法应建立在算法的公开而不影响明文和密文的安全，即密码算法的安全性依赖于对密钥的保密。
  • 这一原则已得到普遍承认，成为判定 密码强度的衡量标准， 也成为 古典密码和现代密码的分界线之一。

现代密码阶段

现代密码I阶段（密钥密码）

• 时间跨度：1949年-1976年
• 1949年香农：《保密系统的信息理论（The Communication Theory of Secret Systems）》
  • 定义了理论安全性，提出扩散和混淆原则
  • 奠定了密码学的理论基础
  • 艺术 ——> 科学
• 里程碑事件：
  • 1949年香农的“保密系统的信息理论”
  • 1967年Kahn的“The Codebreakers”
  • 1971-73年IBM的Feistel等的几篇技术报告
  • Lucifer ——> DES
• 保密性：
  • 数据的安全基于密钥而不是算法的保密。

现代密码II阶段（公钥密码）

• 时间跨度：1976年-1994年
• 里程碑事件：
  • 1976年Diffie和Hellman的“New Directions in Cryptography”提出了公钥密码的概念
  • 1977年Rivest、Shamir、Adleman提出了RSA公钥算法
  • 1977年，DES成为第一代公开的，完全说明细节的商业级密码标准
  • 90年代逐步出现椭圆曲线等其他公钥算法
• 公钥密码部分解决了对称密钥密码算法密钥共享和密钥管理困难的问题。
• 特点：
  • 对称密钥加密算法进一步发展，加密算法更加复杂，以DES为代表的加密算法正式成为行业标准
  • 第二把加密密钥“公钥”开始出现，以RSA加密算法为代表的公开密钥加密算法开始流行
  • 以Hash算法为代表的解决数据完整性的数据摘要算法也开始出现。

现代密码III阶段

• 时间区域：1994年至未来
• 里程碑：
  • 1994年，Shor提出量子计算机模型下分解大整数和求解离散对数的多项式时间算法
  • 2000年，AES正式取代DES成为了新的加密标准
  • 2006年，第一届后量子密码学国际研讨会召开
  • 2017年，NIST开始征集后量子密码标准

未来展望（后量子公钥密码）

• 后量子密码：
  • 基于编码的公钥密码
  • 基于格的公钥密码
  • 基于Hash的公钥密码
  • 基于多变量的公钥密码

密码分析学

安全的定义

安全的概念

Bruce Schneier说过：“如果把一封信锁在保险柜中，把保险柜藏起来，然后告诉你去看这封信，这并不是安全，而是 隐藏。 相反，如果把一封信锁在保险柜中，然后把保险柜及其设计规范和许多同样的保险柜给你，以便你和世界上最好的开保险柜的专家都能够研究锁的装置，而你还是无法打开保险柜去读这封信，这才是 安全。
Bruce Schneier的这段话符合了Kerckhoffs假设的约定。

密码分析学的前提

• Kerckhoffs假设：假定密码分析者和敌手知道所使用的密码系统。即密码体制的安全性仅依赖于对 密钥的保密（一切秘密皆蕴含在密钥中），而不应依赖于算法的保密。
  • 假设敌手知道：
    1. 所使用的加密算法
    2. 知道明文的概率分布规律
    3. 知道密钥的概率分布
    4. 知道所有可能的破译方法
    5. 敌手能够拿到加密装置，可以对其进行能量消耗分析等

密码分析学的目标

• 恢复合法密文相应的明文
• 恢复密钥

密码分析方法的分类

密码体制的攻击方法分类

• 穷举攻击：通过穷举所有的密钥来进行破译
  • 对抗：通过增大密钥的数量
• 统计分析攻击：通过分析密文和明文的统计规律来破译
  • 对抗：设法使明文和密文的统计规律不一样
• 解密变换攻击：针对加密变换的数字基础，通过数学求解设法找到解密变换
  • 对抗：选用具有坚实数学基础和足够复杂的加密算法

根据可获得密码分析的信息量分类

• 唯密文攻击（仅知道一些密文）
• 已知明文攻击（知道一些密文和明文）
• 选择明文攻击（密码分析者可以选择一些明文并得到相应的密文）
• 选择密文攻击（密码分析者可以选择一些密文并得到相应的明文）

唯密文攻击

• 密码分析者仅知道一些密文
• 最困难，一般是穷搜索，对截获密文用所有可能密钥去试
• 唯密文攻击敌手知道的信息量最少，最易抵抗
• 只要有足够的计算时间和存储容量，原则上可成功，但在实际上一种能保证安全要求的实用密码算法，都会设计得使得该方法在实际上不可行
• 一般的敌手需要对密文进行统计测试分析，为此需要知道被加密的明文类型，文本，图像等。

已知明文攻击

• 密码分析者知道一些明文和相应的密文
• 在很多情况下，敌手可能由更多的信息，也许能够截获一个或多个明文及其对应的密文，或消息中将出现某种明文格式，这时的攻击称为已知明文攻击，敌手也许能从已知的明文将变换成密文的方式得到密钥

选择明文攻击

• 密码分析者可以选择一些明文，并得到相应的密文。
• 如果攻击者能在加密系统中插入自己选择的明文消息，则通过该明文消息对应的密文可能确定出密钥的结构。
• 明文可以是精心选择的

选择密文攻击

• 密码分析者可以选择一些密文，并得到相应的明文。
• 攻击者利用解密算法，对自己所选的密文解密出相应的明文，有可能确定出密钥信息。
• 选择的密文可以与破解的密文相关。

无条件安全与计算上安全

• 无条件安全（不可破译的）：
  • 无论截获多少密文，都没有足够信息来唯一确定明文，则该密码是无条件安全的。即对算法的破译不必猜测有优势。
• 计算上安全的：
  • 使用有效资源对一个密码系统进行分析而未能破译，则该密码是强的或计算上安全的。

密码算法要满足的准则

密码算法只要满足以下两条准则之一，即在实际中是可用的：

• 破译密文的代价超过被加密信息的价值
• 破译密文所花的时间超过信息的有用期

古典密码算法

置换（Permutation）密码

• 对明文字符或字符组进行位置移动的密码
• 明文的字母保持相同，但顺序被打乱了

天书（Scytale）

• 500.B.C.，斯巴达人在军事上用于加解密
  • 发送者把一条羊皮纸螺旋形的缠在一个圆柱形木棒上，核心思想是置换（木棒的直径需要保密）

代替（Substitution）密码

• 代替密码构造一个或多个密文字母表，然后用密文字母表中的字母或者字母组来代替明文字母或字母组，各字母或字母组的相对位置不变，但其本身的值改变了。
• 代替密码分为单表代替密码和多表代替密码。

单表代替密码

单表代替密码可分为：

• 加法密码
• 乘法密码
• 仿射密码

单表代替密码——加法密码

$$y=x+k(mod26)$$

• 明文：$x$
• 密文：$y$
• 密钥：$k$
• 解密：$x=y-k(mod26)$

凯撒（Caeaser）密码（k=3）

明文字母	A	B	C	D	E	F	G	H	I	J	K	L	M	N	O	P	Q	R	S	T	U	V	W	X	Y	Z
密文字母	D	E	F	G	H	I	J	K	L	M	N	O	P	Q	R	S	T	U	V	W	X	Y	Z	A	B	C

• 设明文为：FOCUS
• 则密文为：IRFXV

单表代替密码——乘法密码

$$y=kx(mod26)$$

• 明文：$x$
• 密文：$y$
• 密钥：$k$
• 解密：$x=k^{-1}y(mod26)$
• 条件：$(k,26)=1$

乘法密码的关键在于求解$k^{-1}$：
方法：扩展的欧几里得算法
若$(m,n)=1$，则存在整数$k_1,k_2$使得$k_{1}m+k_{2}n=1$
这里$k1$就是$m^{-1}modn$，
注意要将$k1$变为正数：
$$-k_{1}modn=(n-k1)modn$$

单表代替密码——仿射密码

• 加密函数：$y=ax+b(mod26)$
• 密钥：$a,b$
• 解密函数：$x=a^{-1}(y-b)(mod26)$
• 条件：$(a,26)=1$
• 仿射密码是乘法密码和加法密码的结合。

单表代替的统计分析

单表代替密码的特点是相同的明文被加密成相同的密文，这使得针对单表代替密码的统计分析可能破译该密码。
以英文为例，英文中字母出现的频率是有规律的，只要能够收集足够多的密文，通过统计就能够很容易地进行密码的破译。

多表代替密码

多表代替密码首先将明文$M$分为由$n$个字母构成的分组$M_1,M_2,\cdot \cdot \cdot ,M_j$，对每个分组$M_i$的加密为：
$$C_i\equiv A{M}_i+B(modN),i=1,2,\cdot \cdot \cdot ,j$$
其中$(A,B)$是密钥，$A$是$n\times n$的可逆矩阵，满足$gcd(|A|,N)=1$（$|A|$是行列式），$B=(B_1,B_2,\cdot \cdot \cdot ,B_n{)}^T$，$C=(C_1,C_2,\cdot \cdot \cdot ,C_n{)}^T$，$M_i=(m_1,m_2,\cdot \cdot \cdot ,m_n{)}^T$
对密文分组$C_i$的解密为：
$$M_i\equiv A^{-1}(C_i-B)(modN),i=1,2,\cdot \cdot \cdot ,j$$

多表代替密码示例

设$n=3,N=26$
$$A=\left(\begin{array}{ccc}11& 2& 19\\ 5& 23& 25\\ 20& 7& 17\end{array}\right),B=\left(\begin{array}{c}0\\ 0\\ 0\end{array}\right)$$
明文为”YOUR PIN NO IS FOUR ONE TWO SIX”

加密

将明文分为$n=3$个字母组成的分组“YOU RPI NNO ISF OUR ONE TWO SIX”，
由表：

字母	A	B	C	D	E	F	G	H	I	J	K	L	M	N	O	P	Q	R	S	T	U	V	W	X	Y	Z
数字	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25
得：
$$
M_1 =
\left ( \begin{array}{c}
24 \
14 \
20 \
\end{array}\right),
M_2 =
\left ( \begin{array}{c}
17 \
15 \
8 \
\end{array}\right),
M_3 =
\left ( \begin{array}{c}
13 \
13 \
14 \
\end{array}\right),
M_4 =
\left ( \begin{array}{c}
8 \
18 \
5 \
\end{array}\right),\
M_5 =
\left ( \begin{array}{c}
14 \
20 \
17 \
\end{array}\right),
M_6 =
\left ( \begin{array}{c}
14 \
13 \
4 \
\end{array}\right),
M_7 =
\left ( \begin{array}{c}
19 \
22 \
14 \
\end{array}\right),
M_8 =
\left ( \begin{array}{c}
18 \
8 \
23 \
\end{array}\right)
$$
所以：
$$
C_1 = A
\left ( \begin{array}{c}
24 \
14 \
20 \
\end{array}\right)
(mod\ 26) =
\left ( \begin{array}{c}
22 \
6 \
8 \
\end{array}\right),
C_2 = A
\left ( \begin{array}{c}
17 \
15 \
8 \
\end{array}\right)
(mod\ 26) =
\left ( \begin{array}{c}
5 \
6 \
9 \
\end{array}\right),\
C_3 = A
\left ( \begin{array}{c}
13 \
13 \
14 \
\end{array}\right)
(mod\ 26) =
\left ( \begin{array}{c}
19 \
12 \
17 \
\end{array}\right),
C_4 = A
\left ( \begin{array}{c}
8 \
18 \
5 \
\end{array}\right)
(mod\ 26) =
\left ( \begin{array}{c}
11 \
7 \
7 \
\end{array}\right),\
C_5 = A
\left ( \begin{array}{c}
14 \
20 \
17 \
\end{array}\right)
(mod\ 26) =
\left ( \begin{array}{c}
23 \
19 \
7 \
\end{array}\right),
C_6 = A
\left ( \begin{array}{c}
14 \
13 \
4 \
\end{array}\right)
(mod\ 26) =
\left ( \begin{array}{c}
22 \
1 \
23 \
\end{array}\right),\
C_7 = A
\left ( \begin{array}{c}
19 \
22 \
14 \
\end{array}\right)
(mod\ 26) =
\left ( \begin{array}{c}
25 \
15 \
18 \
\end{array}\right),
C_8 = A
\left ( \begin{array}{c}
18 \
8 \
23 \
\end{array}\right)
(mod\ 26) =
\left ( \begin{array}{c}
1 \
17 \
1 \
\end{array}\right)
$$
所以密文为“WGI FGJ LHH XTH WBX ZPS BRB”。

解密

解密时，先求出：
$$A^{-1}={\left(\begin{array}{ccc}11& 2& 19\\ 5& 23& 25\\ 20& 7& 17\end{array}\right)}^{-1}(mod26)=\left(\begin{array}{ccc}10& 23& 7\\ 15& 9& 22\\ 5& 9& 21\end{array}\right)$$
再求：
$$\begin{gathered} M_1=A^{-1}\left(\begin{array}{c}22\\ 6\\ 8\end{array}\right)=\left(\begin{array}{c}24\\ 14\\ 20\end{array}\right),M_2=A^{-1}\left(\begin{array}{c}5\\ 6\\ 9\end{array}\right)=\left(\begin{array}{c}17\\ 15\\ 8\end{array}\right), \\ {M}_3=A^{-1}\left(\begin{array}{c}19\\ 12\\ 17\end{array}\right)=\left(\begin{array}{c}13\\ 13\\ 14\end{array}\right),M_4=A^{-1}\left(\begin{array}{c}11\\ 7\\ 7\end{array}\right)=\left(\begin{array}{c}8\\ 18\\ 5\end{array}\right), \\ {M}_5=A^{-1}\left(\begin{array}{c}23\\ 19\\ 7\end{array}\right)=\left(\begin{array}{c}14\\ 20\\ 17\end{array}\right),M_6=A^{-1}\left(\begin{array}{c}22\\ 1\\ 23\end{array}\right)=\left(\begin{array}{c}14\\ 13\\ 4\end{array}\right), \\ {M}_7=A^{-1}\left(\begin{array}{c}25\\ 15\\ 18\end{array}\right)=\left(\begin{array}{c}19\\ 22\\ 14\end{array}\right),M_8=A^{-1}\left(\begin{array}{c}1\\ 17\\ 1\end{array}\right)=\left(\begin{array}{c}18\\ 8\\ 23\end{array}\right) \end{gathered}$$
得明文为：“YOU RPI NNO ISF OUR ONE TWO SIX”

求$mod26$下的逆矩阵

已知：
$$A=\left(\begin{array}{ccc}11& 2& 19\\ 5& 23& 25\\ 20& 7& 17\end{array}\right)$$
求得：
$$\begin{gathered} |A|(mod26)=-4869(mod26)\equiv 19 \\ 因为19和26互素，所以矩阵A可逆 \\ |A{|}^{-1}(mod26)\equiv 19^{-1}(mod26)\equiv 11 \end{gathered}$$
伴随矩阵
$$A^{\ast }=\left(\begin{array}{ccc}{A}_{11}& A_{21}& A_{31}\\ A_{12}& A_{22}& A_{32}\\ A_{13}& A_{23}& A_{33}\end{array}\right)(mod26)=\left(\begin{array}{ccc}216& 99& -387\\ 415& -193& -180\\ -425& -37& 243\end{array}\right)(mod26)=\left(\begin{array}{ccc}8& 21& 3\\ 25& 15& 2\\ 17& 15& 9\end{array}\right)$$
逆矩阵：
$$A^{-1}=|A{|}^{-1}{A}^{\ast }=11\times \left(\begin{array}{ccc}8& 21& 3\\ 25& 15& 2\\ 17& 15& 9\end{array}\right)(mod26)=\left(\begin{array}{ccc}10& 23& 7\\ 15& 9& 22\\ 5& 9& 21\end{array}\right)$$