Thin Plate Spline （薄板样条函数）

原网址：http://blog.csdn.net/swimmingfish2004/article/details/7666087

对于“Given corresponding points in two images, how do we warp one into the other？”这个问题可以用TPS方法进行纹理映射或者三角面片线性插值算法解决。TPS是什么？以下是一些关于TPS的介绍。

一、from http://hi.baidu.com/wpzhao/item/4ae41f5134950ba9acc8579e

一直不太明白TPS是什么东西，今天特地上网查了一下，总结如下：

1. TPS是一种插值方法，它寻找一个通过所有的控制点的弯曲最小的光滑曲面；就像一个薄铁板，通过所给定的几个“样条”（比如木条），铁板表面是光滑的。弯曲最小由一个能量函数定义，就是wiki上的那个双重积分。

2. 对于3个不共线的控制点，TPS是一个平面，多于三个是一个曲面，少于三个则是未定义的。

3. TPS常用来对形状进行 non-rigid 变形，比如给定原始形状的有限点集A，变形后的对应目标点集B，设C=B-A，对(Ax,Ay, Cx)拟合出一个TPS，就可以得到x方向的内插函数；对(Ax,Ay, Cy)拟合出来的TPS则可以得到y方向的内插函数。这样一以来对于不在点集中的点，我们就可以插值得到目标点。从而完成整个面的变形。

4. 某些情况下数据（控制点坐标）可能存在噪声，这时可能会放松要求，TPS得到的曲面不一定要通过所有的控制点（类比B样条），这就是正则化（regularization ），并由一个正则化参数λ控制。如果λ＝0就是普通的TPS，如果λ为无穷大，TPS就退化为均方误差最小平面（平面的弯曲量为0），对于变形操作来说就是一般的仿射变换。

5. TPS是一种径向基函数，径向基函数主要是用来解决插值问题的，这种函数只与到某个点的距离有关，所以叫径向，又因为它们是函数空间中用来逼近函数的基（类似于多项式函数或三角函数），所以叫径向基。

6. 仿射变换保持点的共线性和直线的平行性，可由平移、旋转、缩放、翻转(Flip)和错切(Shear)变换等原子操作叠加实现。平移、旋转、翻转(Flip)不会改变物体形状，属于刚性(rigid)变换。注意错切变换不是Photoshop中的斜切（只拖动一个控制点），后者不保持直线的平行性。仿射变换是线性的，透视变换不是线性的。

7. 正定阵是可逆的。

8. TPS是非参，有解析解(Closed-form solution)的。

TPS的C++程序示例：http://elonen.iki.fi/code/tpsdemo/
Wiki上的TPS：http://en.wikipedia.org/wiki/Thin_plate_spline
RBF介绍：http://www.farfieldtechnology.com/products/toolbox/theory/rbffaq.html
径向基函数：http://166.111.121.20:9218/fedora/get/mathjourpaper:SXJZ803001/fedora-system:3/getItem?itemID=DS1

二：from http://www.cnblogs.com/xiaotie/archive/2009/10/15/1583730.html

如何测量2个2D形状之间的相似性？2D形状的形变使这个问题变得非常复杂。
很多情况下，我们无法准确的描述这种形变，使用2D插值是一个很好的办法。
TPS（薄板样条）插值是常用的2D插值方法。它的物理意义是：假设在原形状中有N个点An，这N个点在形变之后新坐标之下对应新的N个点Bn。用一个薄钢板的形变来模拟2D形变，确保这N个点能够正确匹配，那么怎样的形变，可以使钢板的弯曲能量最小？TPS插值是这个问题的数值解法。
TPS更详细的描述见F.L. Bookstein, "Principal Warps: Thin-Plate Splines and the Decomposition of Deformations,"

下面是一段TPS插值程序运行结果（代码就不放了，保密）



TPS插值的伟大之处在于，几乎所有的生物有关的形变都可以用TPS来近似。Bookstein本人就是生物形态计量的大师。

TPS插值的前提是：找出特征点。找出特征点的算法有很多种，角点检测，形状上下文，Sift……都可以。

三：from http://help.arcgis.com/zh-cn/arcgisdesktop/10.0/help/index.html#//009z00000078000000

样条函数法的工作原理

Resource Center

样条函数法工具应用的插值方法是利用最小化表面总曲率的数学函数来估计值，从而生成恰好经过输入点的平滑表面。

概念的背景

从概念上讲，采样点被拉伸到它们数量上的高度；样条函数折弯一个橡皮页，该橡皮页在最小化表面总曲率的同时穿过这些输入点。在穿过采样点时，它将一个数学函数与指定数量的最近输入点进行拟合。此方法最适合生成平缓变化的表面，例如高程、地下水位高度或污染程度。

基本形式的最小曲率样条函数插值法在内插法的基础上增加了以下两个条件：

• 表面必须恰好经过数据点。
• 表面必须具有最小曲率 - 通过表面上每个点获得的表面的二阶导数项平方的累积总和必须最小。

基本最小曲率法也称为薄板插值法。它确保表面平滑（连续且可微分），一阶导数表面连续。在数据点的周边，梯度或坡度的变化率（一阶导数）很大；因此，该模型不适合估计二阶导数（曲率）。

通过将权重参数的值指定为 0，可将基本插值法应用到样条函数法工具。

样条函数法类型

有两种样条函数方法：规则样条函数方法和张力样条函数方法。规则样条函数方法使用可能位于样本数据范围之外的值来创建渐变的平滑表面。张力样条函数方法根据建模现象的特性来控制表面的硬度。它使用受样本数据范围约束更为严格的值来创建不太平滑的表面。

规则样条函数类型

REGULARIZED 选项对最小化条件进行了修改，从而将三阶导数项加入到最小化条件中。权重参数指定最小化期间附加到三阶导数项的权重，在文献资料中称为τ (tau)。增大此项的值可以得到更加平滑的表面。介于 0 和 0.5 之间的值比较适合。使用 REGULARIZED 选项可确保获得平滑的表面以及平滑的一阶导数表面。如果需要计算插值表面的二阶导数，此方法很有用。

张力样条函数类型

TENSION 选项对最小化条件进行了修改，从而将一阶导数项加入到最小化条件中。权重参数指定最小化期间附加到一阶导数项的权重，在文献资料中称为 Φ (phi)。权重为零时，将变为基本薄板样条函数插值法。增大权重值将会降低薄板的硬度，在极限情况下，随着 phi 接近无穷大，表面形状将近似于经过这些点的膜或橡皮页。插值的表面很平滑。一阶导数连续但不平滑。

其他样条函数参数

通过以下两个附加参数可以进一步控制输出表面：权重和点数。

权重参数

对于规则样条函数方法，权重参数定义曲率最小化表达式中表面的三阶导数的权重。权重越高，输出表面越平滑。为该参数输入的值必须大于或等于零。可能会用到的典型值有 0、0.001、0.01、0.1 和 0.5。

对于张力样条函数方法，权重参数定义张力的权重。权重越高，输出表面越粗糙。输入的值必须大于或等于零。典型值有 0、1、5 和 10。

点数参数

点数识别在计算每个插值像元时所使用的点数。指定的输入点越多，较远数据点对每个像元的影响就越大，输出表面也就越平滑。点数的值越大，处理输出栅格所需的时间就越长。

样条函数法方程

样条函数法工具的算法为表面插值使用以下公式：

• 其中：

  j = 1, 2, ..., N

  N 为点数。

  λ_j 是通过求解线性方程组而获得的系数。

  r_j 是点 (x,y) 到第j 点之间的距离。

根据所选的选项，T(x,y) 和R(r) 的定义将有所不同。

出于计算目的，输出栅格的整个空间被划分为大小相等的块或区域。x 方向和 y 方向上的区域数相等，并且这些区域的形状均为矩形。将输入点数据集中的总点数除以指定的点数值可以确定区域数。如果数据的分布不太均匀，则这些区域包含的点数可能会明显不同，而点数值只是粗略的平均值。如果任何一个区域中的点数小于八，则该区域将会扩大到至少包含八个点。

对于 REGULARIZED 选项

T(x,y) = a1 + a2x + a3y

• 其中：

  a_i 是通过求解线性方程组而获得的系数。

以及

• 其中：

  r 是点与样本之间的距离。

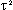   是权重参数。

  K_o 是修正贝塞尔函数。

  c 是大小等于 0.577215 的常数。

对于 TENSION 选项

T(x,y) = a1

• 其中：

  a₁ 是通过求解线性方程组而获得的系数。

以及

• 其中：

  r 是点与样本之间的距离。

  φ² 是权重参数。

  K_o 是修正贝塞尔函数。

  c 是大小等于 0.577215 的常数。

对输出的区域处理

出于计算目的，输出栅格的整个空间被划分为大小相等的块或区域。x 方向和 y 方向上的区域数相等，并且这些区域的形状均为矩形。将输入点数据集中的总点数除以指定的点数值可以确定区域数。如果数据的分布不太均匀，则这些区域包含的点数可能会明显不同，而点数值只是粗略的平均值。如果任何一个区域中的点数小于八，则该区域将会扩大到至少包含八个点。

参考书目

Franke, R. 1982. Smooth Interpolation of Scattered Data by Local Thin Plate Splines.Computer and Mathematics with Appllications.Vol. 8. No. 4. pp.273–281. Great Britain.

Mitas, L., and H. Mitasova. 1988. General Variational Approach to the Interpolation Problem.Computer and Mathematics with Appllications.Vol. 16. No. 12. pp.983–992. Great Britain.

 

 

四：from http://bbs.esrichina-bj.cn/ESRI/viewthread.php?tid=55815&extra=&page=1

前段时间要对气象要素进行插值,翻看了多种方法,做了个PPT报告.对每个方法有简单的介绍极一些总结,不一定都是个人看法,参考了多方书面(sufer,ArcGIS应用教程)以及坛子里,百度上等搜到的资料的看后笔记,有些注了出处有些忘了.截图共享下,也不知有用没用.有错的地方请跟贴指正,谢谢啦!
--------------------------------
所谓空间数据插值,即通过探寻收集到的样点/样方数据的规律,外推/内插到整个研究区域为面数据的方法.即根据已知区域的数据求算待估区域值, 影响插值精度的主要因素就是插值法的选取

空间数据插值方法的基本原理:
任何一种空间数据插值法都是基于空间相关性的基础上进行的。即空间位置上越靠近,则事物或现象就越相似, 空间位置越远,则越相异或者越不相关，体现了事物/现象对空间位置的依赖关系。（http://kc.njnu.edu.cn/dky/nb/page/2000-3-3/2000332117262480.htm，南京师范大学地理科学学院地理信息系统专业网络课程教程）
Ø
由于经典统计建模通常要求因变量是纯随机独立变量，而空间插值则要求插值变量具备某种程度的空间自相关性的具随机性和结构性的区域化变量。即区域内部是随机的，与位置无关的，而在整体的空间分布上又是有一定的规律可循的，这也是不宜用简单的统计分析方法进行插值预估的原因。从而空间统计学应用而生。
Ø
无论用哪种插值方法，根据统计学假设可知，样本点越多越好，而样本的分布越均匀越好。
常用的空间数据插值方法之一：趋势面分析
n
趋势面分析（Trend analyst）。严格来说趋势面分析并不是在一种空间数据插值法。它是根据采样点的地理坐标X，Y值与样点的属性Z值建立多元回归模型，前提假设是，Z值是独立变量且呈正态分布，其回归误差与位置无关。
n
根据自行设置的参数可建立线性、二次…或n次多项式回归模型，从而得到不同的拟合平面，可以是平面，亦可以是曲面。精度以最小二乘法进行验证。
趋势面分析中，将Z值分解成如下等式：

Ø
由于空间数据不具备重复抽样条件，所以通常将后两项合并。趋势值即回归值，而后两项将合并到拟合残差中。
Ø
在趋势面拟合中，空间位置以平面坐标为佳，即将经纬度坐标转换为以米为单位的平面大地坐标。
Ø
通常趋势面分析用于分析趋势和异常而不追求高的拟合精度，一般达到60-80%，阶数在1-4之间即可。拟合精度按R^2系数和F值检验。
由上述可知，趋势面分析是经典统计学在点数据进行空间展面上的应用，属于全局多项式插值，即对整个研究区域用一个多项式进行拟合。

它的缺点在于：当研究区域范围较大，地形很复杂时，需要用高阶多项式拟合以提高精度，但高阶将增加其计算成本，因而需要进行改进。
常用的空间数据插值方法之二：局部多项式插值
局部多项式插值（Local Polynomial Interpolation）：用多个多项式进行拟合。每个多项式都只在特定重叠的邻近区域内有效，通过设定搜索半径和方向的来定义邻近区域。

显然，局部多项式插值是对全局多项式，即趋势面拟合的一大改进。这里涉及到一个搜索邻域的概念。
空间数据插值之邻近区域：
n
从空间自相关性的概念可知，空间上越靠近，属性就越相似，相关性也越高。那么，两个样点间在多远的距离内所具备相关性可以不考虑，或者其相关将消失呢？可以根据经验或专业背景找出这么一个阈值，作为邻近区域的半径。
n
同时，如果其自相关性在不同的方向上消失的距离值也不同的话，将还需要设置一个方向值以及长短两个半径值，此时的邻近区域将呈椭圆。（如当属性值受风向影响较大时，应当将风向角度设置为搜索方向，即长半径所在的方向）
n
通过半径和方向可以定义出一个以待估点为中心的区域（圆或者椭圆）。
n
此外，还可以通过限制参与某待估点值进行预测的样点数来定义邻近区域。即参与某点预测的最多样点数和最少样点数。
n
在由半径和方向决定的区域内包含到的样点数为0时，则扩大搜索区域使其达到最小样点数值。
空间数据插值之各向异性：
在设定邻近区域时，提到了一个方向参数。即当空间相关性沿各个方向上的消失距离都一致时，其邻近区域应该是一个圆，如图a，叫各向同性。否则，如图b，在西南-东北方向上的消失距离明显小于东南-西北方向，则其邻近区域应当是一个平行于东南-西北方向的椭圆，其方向角度（Angle Direction）设为长轴与X轴的角度值。图b的现象即各向异性（Anisotropy)。(图片来源：Arcgis Desjktop Help文件)图中的Range（变程）参数，即自相关消失或不予考虑的半径值。图b中的Minor Range,最小变程，即相关性消失得最快的方向上的半径值，而Major Range，最大变程即相关性消失最慢的方向上的半径值。

常用的空间数据插值方法之三：移动平均插值法（Moving Average)
移动平均插值法，通过设定邻近区域，取该区域内样点的平均值作为待估点的值。

适用于样点分布均匀、密集，而且变化缓慢的情况下，对缺失值进行填补。

主要用于消除随机干扰，即局部降噪功能。

优势在于计算简便快速，但适用范围较窄。
常用的空间数据插值方法之四：线性三角网法（Triangulaion with Linear Interpolation）

线性三角网法是最佳的Delaunay三角形，连续样点数据间的连线形成三角形，覆盖整个研究区域，所有三角形的边都不相交。（即与构建TIN文件的原理一致）

线性三角网法将在整个研究区域内均匀分配数据，地图上的稀疏区域会形成截然不同的三角面。
常用的空间数据插值方法之五：最近邻点插值法（Nearest Neighbor)

最近邻点插值法，又称泰森多边形（Thiessen或Voronoi多边形）分析法。即在每个样点数据周边生成一个邻近区域，即Thiessen多边形，使得每个多边形内的任意一点离其内部的样点最近，在多边形内插值时只有其中心样点参与运算，如图：


最近邻点插值法同样只适用于样点分布均匀、紧密完整，且只有少数缺失值时，对缺失值进行填补

常用的空间数据插值方法之六：自然邻近插值法（Natural Neighbor)

自然邻近插值法是对泰森多边形插值法的改进。它对研究区域内各点都赋予一个权重系数，插值时使用邻点的权重平均值决定待估点的权重。每完成一次估值就将新值纳入原样点数据集重新计算泰松多边形并重新赋权重，再对下一待估点进行估值运算。

对于由样点数据展面生成栅格数据而言，通过设置栅格大小（cell size)来决定自然邻近插值中的泰森多边形的运行次数n，即，设整个研究区域的面积area，则有：n=area/cell size

可设置各向异性参数（半径和方向）来辅助权重系数的计算。

常用的空间数据插值方法之七：反距离权重插值法(Inverse Distance Weighting, IDW)

反距离权重插值综合了泰森多边形的自然邻近法和多元回归渐变方法的长处，在插值时为待估点Z值为邻近区域内所有数据点都的距离加权平均值，当有各向异性时，还要考虑方向权重。

权重函数与待估点到样点间的距离的U次幂成反比，即随着距离增大，权重呈幂函数递减。且对某待估点而言，其所有邻域的样点数的权重和为1。

决定反距离权重插值法结果的参数包括距离的U次幂值的确定，同时还取决于确定邻近区域的所使用的方法。此外，为消除样点数据的不均匀分布的影响，还可设置引入一个平滑参数，以保证没有哪个样点被赋予全部的权重，即使得插值运算时尽可能不只有一个样点参与运算。

IDW是一种全局插值法，即全部样点都参与某一待估点的Z值的估算；

IDW的适用于呈均匀分布且密集程度足以反映局部差异的样点数据集；

IDW与之前介绍的插值法的不同之处在于，它是一种精确的插值法，即插值生成的表面中预测的样点值与实测样点值完全相等。
常用的空间数据插值方法之八：最小曲率法(Minimum Curvature)
最小曲率插值法，非精确插值法。其插值基准是生成一个具有最小曲率（即弯曲度最小），且到各样点的Z值的距离最小的曲面。

影响最小曲率插值法精度的参数有：

最大残差，通常允许残差在10%-1%之间

最大循环次数，与栅格大小（cell size）有关,通常设置为生成的栅格数量的一到两倍。
常用的空间数据插值方法之九：径向基函数插值法（Radial Basis Function)

所谓径向基函数即基函数是由单个变量的函数构成的，是一系列精确插值法的统称。该插值法中的单个变量是指待估点到样点间的距离H，其中每一插值法都是距离H的基函数。

径向基函数是对最小曲率插值的改进，即属于精确的最小曲率插值法。

径向基函数包括的多种函数有：倒转复二次函数（InverseMultiquadric),复对数（Multilog),复二次函数（Multiquadratic),自然三次样条函数（Natural CubicSpline),薄板样条法函数（Thin Plate Spline);

上述的每一函数式中都带有一个平滑因子R，即使得生成的曲面不至于太粗糙。

在实际应用中，许多人都发现复二次函数的效果最佳。

径向基函数比同为精确插值法IDW的优点在于，它可以计算出高于或低于样点Z值的预测值。

通常俗称的样条插值法即径向基函数插值法。此后在实际应用中又发展出了多种样条插值法，包括GRASS软件的RST，RegulationSpline with Tension, ANUSPLINE的薄盘光滑样条插值法；大大提升了样条插值的精度(对气象要素进行插值时推荐该方法,可综合考虑多个协变量,从而大大减少结果的不确定性)。

常用的空间数据插值方法之九：径向基函数插值法（Radial Basis Function)

径向基函数适用于样点数据集大、表面变化平缓的情况；

当局部变异性大，且无法确定样点数据的准确性，或样点数据具很大不确定性时，不适用该技术。
常用的空间数据插值方法之十：地统计插值法（Geostatistical Analyst)

前面提到的多种基于空间统计学的插值方法都属于确定性插值法。

而另一类插值法就是地统计插值法，它是空间统计分析的一个分支。

地统计与确定性插值的最大区别在于，地统计插值引入了概率模型，即地统计插值认为从一个统计模型不可能完全精确地得出预测值，所以在进行预测时，应该给出预测值的误差，即预测值在一定概率内合理。

通常所说的地统计插值是指克里格插值法（Kriging)
Z（s）=μ（s）+ε（s）
S表示不同的位置点，可以是用经纬度表示的空间坐标。
Z（s）是该位置点的属性值。μ（s）为确定趋势值，ε（s）
为自相关随机误差。

当要考虑多个协同变量的情况下，可采用协克里格插值法（Co-Kriging).则其计算公式将变为：
Zj（s）=μj（s）+εj（s）
表示的是第j个变量的情况。在协克里格中，只对主变量进行预估，但将在插值预估时引入不同变量间的随机误差项εj（s）的交叉相关性值，从而构建协同克里格模型。

克里格插值是一个最优的无偏估计法。

获得预测图并不要求数据呈正态分布。但当数据呈正态分布时，克里格插值法将是无偏估计法中效果最好的一种方法。

因此，在进行克里格插值前，可先对非正态分布的数据进行转换，包括Log对数转换，Box-Cox转换，使之呈正态分布，然后再进行插值。
根据样点数据统计特征的不同可将克里格分成多种不同的插值法：

当样点数据是二进制值时，用指示克里格插值法进行概率预测；

对样点数据进行了未知函数变换后，可用该变换函数进行析取克里格插值；

当样点数据的趋势值μ（s）是一个未知常量时，用普通克里格；

当样点数据的趋势可用一个多项式进行拟合，但回归系数未知时，用泛克里格插值法；

当样点数据的趋势已知时，用简单克里格插值法；

其中最常用的是普通克里格与泛克里格插值法；当加入了协变量进行插值时，则叫作协同普通克里格插值法和协同泛克里格插值法。

同反距离权重插值法IDW一样,克里格插值法同样可以表示为:
Z(x0)=∑λi Z(xi)
Z(x0)为待估点的值, Z(xi) 为待估点周围的已知样点值,λi为第i个已知点的权重

所不同之处在于,IDW的权重为待估点与已知样点间距离的u次幂的倒数,而克里格的权重值不仅考虑待估点与已知样点、已知样点之间的距离,还考虑了其空间分布的方位。通过半变异函数来赋权重值。
克里格插值之半变异函数和协方差函数（Semivariogram /covariance）：

半变异函数和协方差函数都是空间自相关性的定量化表达函数。半变异函数的定义为：
r(h)=1/2var(Z(si)-Z(sj))
hij为样点si和 sj间的距离,
Z(si)和Z(sj)分别代表样点的属性值；

若把si和 sj看作一个样点对，r(h)表示的是所有距离为h的样点对的方差的一半。

对于均匀分布的样点数据，任意样点对间的距离都是h的倍数；而一般的样点数据都是随机分布的，则各样点对间的距离有可能是唯一值。为了便于对r(h)计算，可将样点对间的距离分成长为h的n段，位于hn和hn-1之间的样点对都记作一组来求算r(h)值。其中，h叫作步长（lagsize),n叫作步长组（Number of lags)。

步长*步长组的值应该在最大的样点对距离的1/2左右。当r(h)较早到达基台值时，该值适当减小，否则适当增大。根据交叉验证或验证来调试其最优值。

基台值是指半变异函数所能达到的顶点，即样点数据集的最大r(h)值。而理论上当h=0时，r(h)也应当为0，但由于测量误差和微观变异的存在，使得r(h)在h=0时不取零值，此时的值即为块金值。如下图：

原网址：http://blog.csdn.net/summitgao/article/details/46678503

1. 基本数学描述

薄板样条(Thin Plate Spline)映射根据两幅相关图像中的对应控制点集来决定一个变形函数。它寻找通过所有给定点的饶度最小的光滑曲面。“薄板”这个名字的由来，就表示薄板样条是用来近似的仿真一块金属薄片在通过相同的控制点时的行为特征。 
 
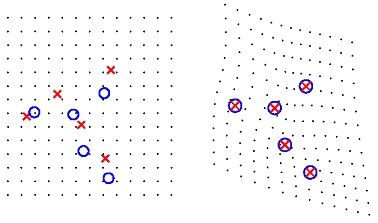
上图是使用薄板样条进行变换的例子，薄板样条插值可表示为多变量插值问题，对于 d 维空间中提取出的 n 个特征点对 xi 和 yi ,问题描述为在一个合适的Hilbert空间 H 上寻找连续变换 f:Rd→Rd ,并满足如下两个条件: 
（1）使得既定泛函 E(f):H→R 最小化; 
（2）满足插值条件(通过指定的几个点)。 
(这里有一系列的数学推导，一维如何计算，二维如何计算，三维如何计算，四维如何计算，暂时代过 … …)

2. 二维图像配准中的应用

以二维图像配准为例,在2维2阶导数情况下,则 f(x,y) 在满足插值方程的同时使得能量函数达到最小，即有： 

f=argminfEfE(f)=∫∫⎛⎝(∂2f∂x2)2+2(∂2f∂x∂y)2+(∂2f∂y2)⎞⎠dxdy

此即为Bookstein于1989年首次将薄板样条应用于二维图像配准中时所采用的目标函数.使得能量函数取得最优解的 f(x,y) 的表达式为： 

f(x,y)=a1+axx+ayy+∑i=1nwiU(∥(xi,yi)−(x,y)∥)

其中 U(r)=r2logr 为径向基函数。 wi,i=1,2,⋯,n 以及 a1,ax,ay 为未知系数。 
为了使 f(x,y) 的二阶导数平方可积，必须有： 

∑i=1nwi=∑i=1nwixi=∑i=1nwiyi=0

故可得薄板样条函数的系数满足一个线性方程组： 

[KPTPO][wa]=[vo]

其中 Ki,j=U(∥(xi,yi)−(xj,yj)∥) ， P 的第i行为 (1,xi,yi) ， O 为 3×3 的零矩阵， o 为 3×1 零向量， w 和 v 为由 wi 和 vi 得到的列向量，而列向量 a 中元素为 a1,ax,ay 。令 

L=[KPTPO]

对上述线性方程组求解，可得： 

w=L−1M

薄板样条的映射函数可以确定源图像（图像A）到目标图像（图像B）的映射变换关键系数 (w1,w2,⋯,wn;a1,ax,ay) ，然后将图像A中任意一点的坐标代入公式，可得到图像B中对应点的坐标。但是，薄板映射并不是一对一的，通常若干个点会映射到同一个点上。这就需要对整幅图像进行遍历，找到所有漏掉的点，通过插值得到这些点的像素值。插值的过程这里不再过多介绍。

3. 结合Matlab代码说明

这里使用的是 Fitzgerald Archibald 的 Matlab 代码来说明，链接如下： 
http://www.mathworks.com/matlabcentral/fileexchange/24315-warping-using-thin-plate-splines

主函数如下，基中，Xp和Yp分别指源图像中的特征点，Xs和Ys指参考图像中的特征点：

%% Algebra of Thin-plate splines
% Compute thin-plate spline mapping [W|a1 ax ay] using landmarks
[wL]=computeWl(Xp, Yp, NPs);
% Y = ( V| 0 0 0)'   where V = [G] where G is landmark homologous (nx2) ; 
% Y is col vector of length (n+3)
wY = [Xs(:) Ys(:); zeros(3,2)]; 
wW = inv(wL)*wY; % (W|a1 ax ay)' = inv(L)*Y
% Thin-plate spline mapping (Map all points in the plane)
% f(x,y) = a1 + ax * x + ay * y + SUM(wi * U(|Pi-(x,y)|)) for i = 1 to n
[Xw, Yw]=tpsMap(wW, imgH, imgW, Xp, Yp, NPs);
 
   
   
   
   

    
    
    
    
1
    
    
    
    
2
    
    
    
    
3
    
    
    
    
4
    
    
    
    
5
    
    
    
    
6
    
    
    
    
7
    
    
    
    
8
    
    
    
    
9
    
    
    
    
10
   
   
   
   
 
   
   
   
   

    
    
    
    
1
    
    
    
    
2
    
    
    
    
3
    
    
    
    
4
    
    
    
    
5
    
    
    
    
6
    
    
    
    
7
    
    
    
    
8
    
    
    
    
9
    
    
    
    
10
   
   
   
   

从中可以看出，首先是计算 L 矩阵，代码如下：

%% [L] = [[K P];[P' 0]]
% np - number of landmark points
% (xp, yp) - coordinate of landmark points
function [wL]=computeWl(xp, yp, np)
   rXp = repmat(xp(:),1,np); % 1xNp to NpxNp
   rYp = repmat(yp(:),1,np); % 1xNp to NpxNp
   wR = sqrt((rXp-rXp').^2 + (rYp-rYp').^2); % compute r(i,j)
   wK = radialBasis(wR); % compute [K] with elements U(r)=r^2 * log (r^2)
   wP = [ones(np,1) xp(:) yp(:)]; % [P] = [1 xp' yp'] where (xp',yp') are n landmark points (nx2)
   wL = [wK wP;wP' zeros(3,3)]; % [L] = [[K P];[P' 0]]
return
 
   
   
   
   

    
    
    
    
1
    
    
    
    
2
    
    
    
    
3
    
    
    
    
4
    
    
    
    
5
    
    
    
    
6
    
    
    
    
7
    
    
    
    
8
    
    
    
    
9
    
    
    
    
10
    
    
    
    
11
   
   
   
   
 
   
   
   
   

    
    
    
    
1
    
    
    
    
2
    
    
    
    
3
    
    
    
    
4
    
    
    
    
5
    
    
    
    
6
    
    
    
    
7
    
    
    
    
8
    
    
    
    
9
    
    
    
    
10
    
    
    
    
11
   
   
   
   

得以 L 矩阵后，下面一行代码用来对 w 求解：

wW = inv(wL)*wY; 
 
   
   
   
   

    
    
    
    
1
   
   
   
   
 
   
   
   
   

    
    
    
    
1
   
   
   
   

最后利用下面一行代码实现源图像到目标图像的变换：

[Xw, Yw]=tpsMap(wW, imgH, imgW, Xp, Yp, NPs);
 
   
   
   
   

    
    
    
    
1
   
   
   
   
 
   
   
   
   

    
    
    
    
1
   
   
   
   

其中，tpsMap的代码如下：

%% Mapping: f(x,y) = a1 + ax * x + ay * y + SUM(wi * U(|Pi-(x,y)|)) for i = 1 to n
% np - number of landmark points
% (xp, yp) - coordinate of landmark points
function [Xw, Yw]=tpsMap(wW, imgH, imgW, xp, yp, np)

[X Y] = meshgrid(1:imgH,1:imgW); % HxW
X=X(:)'; % convert to 1D array by reading columnwise (NWs=H*W)
Y=Y(:)'; % convert to 1D array (NWs)
NWs = length(X); % total number of points in the plane

% all points in plane
rX = repmat(X,np,1); % Np x NWs
rY = repmat(Y,np,1); % Np x NWs

% landmark points
rxp = repmat(xp(:),1,NWs); % 1xNp to Np x NWs
ryp = repmat(yp(:),1,NWs); % 1xNp to Np x NWs

% Mapping Algebra
wR = sqrt((rxp-rX).^2 + (ryp-rY).^2); % distance measure r(i,j)=|Pi-(x,y)|

wK = radialBasis(wR); % compute [K] with elements U(r)=r^2 * log (r)
wP = [ones(NWs,1) X(:) Y(:)]'; % [P] = [1 x' y']'
wL = [wK;wP]'; % [L] = [w1 w2 ... wn 1 x y] 

Xw  = wL*wW(:,1); % [Pw] = [L]*[W]
Yw  = wL*wW(:,2); % [Pw] = [L]*[W]
return

薄板样条插值用于图像配准的原理是非常容易理解的。此外，代码中还有一些是用于插值填图像孔洞 ，这里就不介绍了

注意：这个代码中的X，Y和我们传统图像处理中的X，Y是反的，也就是说，X是行，Y是列，作者为什么这么写，不清楚了

其它细节可以参考如下论文：

1. F.L. Bookstein, “Principal Warps: Thin-Plate Splines and the Decomposition of Deformations,” IEEE TPAMI, 1989.
2. 张春生, 基于CT图像的肺部轮廓非刚性配准方法[D], 哈尔滨工业大学 2012.
3. 李菁菁, 基于控制点平滑的人脸变形算法及其在人脸动画中的应用[D], 湘潭大学 2008.