两种分类方法的比较

一个物体既可以按照元素分类法去分类，也可以按照形态分类法去分类。但似乎很难用元素去分类形态，也很难用形态去分类元素。

想用元素分类形态就得加入位置变量。而所谓的位置变量显然是一种空间变量。是粒子在空间中，所以所谓的空间变量似乎并不是粒子的内在属性，是独立于粒子的一种外部的属性。

同样想用形态去分类元素就需要相对长时间的分布平均值，也就是需要加入时间变量。同样似乎也没有理由认为时间是一种形态的内在属性。所以用形态去分类元素也需要一种外部的属性。

但用这两种方法描述的是同一个物体，所以得到了一个等式

 基于核电荷数表达的元素是一维的和时间一样，而形态是三维的和空间一样。一个是在空间中运动的元素，一个是在时间中运动的形态，一个标记了时间，一个标记了空间。所以这两种分类方法表达的是空间和时间的对称性吗？

这次继续用质心和标准差的方法去拟合迭代次数。

( A, B )---1*30*2---( 1, 0 )( 0, 1 )

让网络的输入只有1个节点，AB各由9张二值化的图片组成.A全是0，B中有4个1，得到迭代次数表格。

0	1	2	3	4	5	6	7	8	迭代次数			A-B
1b	1b	1b	0	1b	0	0	0	0	39477.176	4	4+h5	0*0*0*0*0*0*0*0*0-1*1*1*0*1*0*0*0*0
1b	1b	0	1b	1b	0	0	0	0	40518.643	4	4+h3	0*0*0*0*0*0*0*0*0-1*1*0*1*1*0*0*0*0
1b	1b	1b	0	0	0	0	1b	0	40785.457	4	4+h1	0*0*0*0*0*0*0*0*0-1*0*1*1*1*0*0*0*0
1b	1b	1b	0	0	1b	0	0	0	40695.387	4	4+h4	0*0*0*0*0*0*0*0*0-1*1*1*0*0*1*0*0*0
1b	1b	1b	0	0	0	1b	0	0	41968.141	4	4+h2	0*0*0*0*0*0*0*0*0-1*1*1*0*0*0*1*0*0
1b	1b	0	1b	0	1b	0	0	0	41867.829	4	4+h12	0*0*0*0*0*0*0*0*0-1*1*0*1*0*1*0*0*0
1b	1b	0	1b	0	0	0	1b	0	42412.422	4	4+h9	0*0*0*0*0*0*0*0*0-1*1*0*1*0*0*0*1*0
1b	1b	0	0	0	1b	1b	0	0	42661.869	4	4+h8	0*0*0*0*0*0*0*0*0-1*1*0*0*1*1*0*0*0
1b	1b	0	1b	0	0	1b	0	0	43035.025	4	4+h11	0*0*0*0*0*0*0*0*0-1*1*0*1*0*0*1*0*0
1b	1b	0	0	0	1b	0	1b	0	43201.327	4	4+h6	0*0*0*0*0*0*0*0*0-1*1*0*0*0*1*0*1*0
1b	1b	0	0	1b	0	0	1b	0	43607.116	4	4+h7	0*0*0*0*0*0*0*0*0-1*1*0*0*1*0*0*1*0
1b	1b	0	0	1b	0	1b	0	0	43949.95	4	4+h10	0*0*0*0*0*0*0*0*0-1*1*0*0*1*0*1*0*0
1b	0	1b	0	1b	0	1b	0	0	44721.779	4	4+h13	0*0*0*0*0*0*0*0*0-1*0*1*0*1*0*1*0*0

首先计算质心

1b

1b

0

0

1b

0

0

1b

0

分成两步

1b

1b

0

0

1b

2*x=(4-0.5-x)

X=1.17，质心为1.17+0.5=1.67

第二步计算总的质心

3*x=(7-0.5-1.16666666666667-x)

X=1.33.则总的质心为0.5+1.16666666666667+1.33333333333333=3

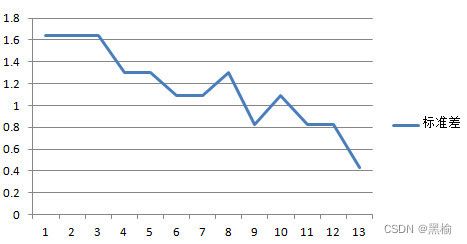
计算标准差，这次用一种更为通用的方法去计算标准差

1b

1b

1b

0

1b

0

0

0

0

					标准差
0	0	1	4		1.6394

4个1b之间的间距是0，0，1，4，标准差为1.6394.

得到表格

0	1	2	3	4	5	6	7	8	迭代次数			质心	间距				标准差	1/标准差	质心+1/标准差
1b	1b	1b	0	1b	0	0	0	0	39477.176	4	4+h5	1.75	0	0	1	4	1.6394	0.609994	2.359994281	0*0*0*0*0*0*0*0*0-1*1*1*0*1*0*0*0*0
1b	1b	0	1b	1b	0	0	0	0	40518.643	4	4+h3	2	0	1	0	4	1.6394	0.609994	2.609994281	0*0*0*0*0*0*0*0*0-1*1*0*1*1*0*0*0*0
1b	1b	1b	0	0	0	0	1b	0	40785.457	4	4+h1	2.5	0	0	4	1	1.6394	0.609994	3.109994281	0*0*0*0*0*0*0*0*0-1*0*1*1*1*0*0*0*0
1b	1b	1b	0	0	1b	0	0	0	40695.387	4	4+h4	2	0	0	2	3	1.299	0.7698	2.769800359	0*0*0*0*0*0*0*0*0-1*1*1*0*0*1*0*0*0
1b	1b	1b	0	0	0	1b	0	0	41968.141	4	4+h2	2.25	0	0	2	3	1.299	0.7698	3.019800359	0*0*0*0*0*0*0*0*0-1*1*1*0*0*0*1*0*0
1b	1b	0	1b	0	1b	0	0	0	41867.829	4	4+h12	2.25	0	1	1	3	1.0897	0.917663	3.167662935	0*0*0*0*0*0*0*0*0-1*1*0*1*0*1*0*0*0
1b	1b	0	1b	0	0	0	1b	0	42412.422	4	4+h9	2.75	0	1	3	1	1.0897	0.917663	3.667662932	0*0*0*0*0*0*0*0*0-1*1*0*1*0*0*0*1*0
1b	1b	0	0	0	1b	1b	0	0	42661.869	4	4+h8	3	0	3	0	2	1.299	0.7698	3.769800359	0*0*0*0*0*0*0*0*0-1*1*0*0*1*1*0*0*0
1b	1b	0	1b	0	0	1b	0	0	43035.025	4	4+h11	2.5	0	1	2	2	0.8292	1.206045	3.706045375	0*0*0*0*0*0*0*0*0-1*1*0*1*0*0*1*0*0
1b	1b	0	0	0	1b	0	1b	0	43201.327	4	4+h6	3.25	0	3	1	1	1.0897	0.917663	4.167662935	0*0*0*0*0*0*0*0*0-1*1*0*0*0*1*0*1*0
1b	1b	0	0	1b	0	0	1b	0	43607.116	4	4+h7	3	0	2	2	1	0.8292	1.206045	4.206045378	0*0*0*0*0*0*0*0*0-1*1*0*0*1*0*0*1*0
1b	1b	0	0	1b	0	1b	0	0	43949.95	4	4+h10	2.75	0	2	1	2	0.8292	1.206045	3.956045378	0*0*0*0*0*0*0*0*0-1*1*0*0*1*0*1*0*0
1b	0	1b	0	1b	0	1b	0	0	44721.779	4	4+h13	3	1	1	1	2	0.433	2.309401	5.309401077	0*0*0*0*0*0*0*0*0-1*0*1*0*1*0*1*0*0

 

迭代次数和质心成正比

 

迭代次数和标准差成反比

用标准差的倒数去修正质心的数据得到曲线y=质心+1/标准差

 

曲线y和迭代次数成正比，平滑很多。

数据

1b	0	0	0	0	0	1b	1b	1b	38034.7	4
0	0	0	0	1b	1b	1b	1b	0	38064.89	4
0	1b	1b	1b	1b	0	0	0	0	38075.63	4
0	0	0	0	0	1b	1b	1b	1b	38150.92	4
1b	1b	0	0	0	0	0	1b	1b	38178.89	4
0	0	1b	1b	1b	1b	0	0	0	38215.21	4
1b	1b	1b	0	0	0	0	0	1b	38222.41	4
0	0	0	1b	1b	1b	1b	0	0	38381.92	4
1b	1b	0	1b	0	0	0	0	1b	39470.74	4+h5
1b	1b	1b	0	1b	0	0	0	0	39477.18	4+h5
0	0	1b	1b	1b	0	1b	0	0	39590.89	4+h5
1b	0	0	0	0	1b	1b	1b	0	39596.71	4+h5
0	0	0	0	1b	1b	1b	0	1b	39630.62	4+h5
1b	0	1b	0	0	0	0	1b	1b	39655.98	4+h5
0	0	0	1b	1b	1b	0	1b	0	39659.56	4+h5
0	1b	1b	1b	0	1b	0	0	0	39696.35	4+h5
0	1b	0	0	0	0	1b	1b	1b	39733.4	4+h5
0	0	1b	1b	0	1b	1b	0	0	40364.98	4+h3
0	1b	1b	0	0	0	0	1b	1b	40397.87	4+h3
1b	0	0	0	0	1b	1b	0	1b	40414.13	4+h3
0	0	0	0	1b	1b	0	1b	1b	40443.07	4+h3
0	1b	1b	0	1b	1b	0	0	0	40462.3	4+h3
1b	1b	0	0	0	0	1b	1b	0	40489.76	4+h3
1b	1b	0	1b	1b	0	0	0	0	40518.64	4+h3
0	0	0	1b	1b	0	1b	1b	0	40525.64	4+h3
1b	1b	0	0	0	0	1b	0	1b	40600.29	4+h1
1b	0	1b	1b	0	0	0	0	1b	40614.69	4+h3
0	0	0	1b	0	1b	1b	1b	0	40669.64	4+h1
1b	1b	0	0	1b	0	0	0	1b	40680.36	4+h4
0	1b	0	0	0	1b	1b	1b	0	40685.67	4+h4
1b	1b	1b	0	0	1b	0	0	0	40695.39	4+h4
0	1b	1b	1b	0	0	0	0	1b	40718.44	4+h1
0	1b	0	1b	1b	1b	0	0	0	40738.36	4+h1
1b	0	0	1b	0	0	0	1b	1b	40747.02	4+h4
0	0	0	1b	1b	1b	0	0	1b	40774.38	4+h4
1b	1b	1b	0	0	0	0	1b	0	40785.46	4+h1
1b	0	1b	1b	1b	0	0	0	0	40794.88	4+h1
0	0	0	0	1b	0	1b	1b	1b	40800.17	4+h1
0	0	1b	0	1b	1b	1b	0	0	40816.7	4+h1
1b	0	0	0	1b	1b	1b	0	0	40821.25	4+h4
0	1b	1b	1b	0	0	1b	0	0	40833.61	4+h4
0	0	1b	1b	1b	0	0	1b	0	40855.6	4+h4
0	0	1b	0	0	0	1b	1b	1b	40931.26	4+h4
1b	0	0	0	0	1b	0	1b	1b	40941.11	4+h1
0	0	0	1b	0	0	1b	1b	1b	41590.38	4+h2
0	1b	0	0	0	1b	1b	0	1b	41739.26	4+h12
1b	0	0	0	1b	1b	0	1b	0	41748.74	4+h12
1b	0	1b	0	0	0	1b	1b	0	41775.63	4+h12
1b	0	0	0	1b	0	0	1b	1b	41796.71	4+h2
0	1b	1b	0	1b	0	1b	0	0	41835.91	4+h12
0	1b	0	0	1b	1b	1b	0	0	41861.36	4+h2
1b	1b	0	1b	0	1b	0	0	0	41867.83	4+h12
1b	1b	0	0	0	1b	0	0	1b	41882.02	4+h2
0	1b	1b	1b	0	0	0	1b	0	41889.73	4+h2
0	1b	0	1b	0	0	0	1b	1b	41897.48	4+h12
1b	0	1b	0	1b	0	0	0	1b	41922.54	4+h12
1b	0	0	1b	1b	1b	0	0	0	41943.03	4+h2
0	0	1b	0	0	1b	1b	1b	0	41948.11	4+h2
1b	1b	1b	0	0	0	1b	0	0	41968.14	4+h2
0	0	1b	1b	0	1b	0	1b	0	41987.61	4+h12
0	0	0	1b	1b	0	1b	0	1b	42030.67	4+h12
0	0	1b	1b	1b	0	0	0	1b	42043.6	4+h2
1b	0	1b	1b	0	1b	0	0	0	42119.11	4+h9
1b	0	0	0	1b	0	1b	1b	0	42250.48	4+h9
0	0	0	1b	0	1b	1b	0	1b	42272.18	4+h9
0	1b	0	0	0	1b	0	1b	1b	42282.24	4+h9
0	1b	0	1b	1b	0	1b	0	0	42297.94	4+h9
1b	0	1b	0	0	0	1b	0	1b	42342.04	4+h9
1b	1b	0	1b	0	0	0	1b	0	42412.42	4+h9
0	1b	1b	0	1b	0	0	0	1b	42417.5	4+h9
0	0	1b	0	1b	1b	0	1b	0	42432.81	4+h9
1b	1b	0	0	1b	1b	0	0	0	42514.65	4+h8
0	1b	1b	0	0	1b	1b	0	0	42547.77	4+h8
0	0	1b	1b	0	0	1b	1b	0	42601.33	4+h8
1b	0	0	0	1b	1b	0	0	1b	42646.66	4+h8
1b	1b	0	0	0	1b	1b	0	0	42661.87	4+h8
0	0	1b	1b	0	0	0	1b	1b	42719.69	4+h8
0	1b	1b	0	0	0	1b	1b	0	42767.35	4+h8
1b	0	0	1b	1b	0	0	0	1b	42781.3	4+h8
0	0	0	1b	1b	0	0	1b	1b	42890.42	4+h8
0	0	1b	1b	0	1b	0	0	1b	42908.32	4+h11
0	1b	1b	0	1b	0	0	1b	0	42954.08	4+h11
1b	1b	0	1b	0	0	1b	0	0	43035.03	4+h11
0	1b	0	0	1b	0	0	1b	1b	43036.09	4+h11
1b	0	0	1b	1b	0	1b	0	0	43040.57	4+h11
1b	0	0	1b	0	0	1b	1b	0	43044.13	4+h11
0	0	1b	0	0	1b	1b	0	1b	43049.19	4+h11
0	1b	0	0	1b	1b	0	1b	0	43117.74	4+h11
1b	1b	0	0	0	1b	0	1b	0	43201.33	4+h6
1b	0	1b	0	0	1b	0	0	1b	43214.11	4+h11
0	1b	1b	0	0	0	1b	0	1b	43260.58	4+h6
0	0	0	1b	0	1b	0	1b	1b	43264.8	4+h6
0	0	1b	0	1b	0	1b	1b	0	43307.4	4+h6
0	1b	0	1b	0	1b	1b	0	0	43311.28	4+h6
1b	0	1b	0	1b	1b	0	0	0	43325.11	4+h6
1b	0	0	0	1b	0	1b	0	1b	43338.26	4+h6
0	1b	0	1b	1b	0	0	0	1b	43366.07	4+h6
1b	0	1b	1b	0	0	0	1b	0	43421.87	4+h6
1b	0	0	1b	0	0	1b	0	1b	43546.95	4+h7
0	0	1b	0	0	1b	0	1b	1b	43593.53	4+h7
1b	1b	0	0	1b	0	0	1b	0	43607.12	4+h7
0	1b	0	1b	1b	0	0	1b	0	43651.83	4+h7
1b	0	0	1b	0	1b	1b	0	0	43652.3	4+h7
0	0	1b	0	1b	1b	0	0	1b	43683.95	4+h7
0	1b	0	0	1b	0	1b	1b	0	43751.72	4+h7
1b	0	1b	1b	0	0	1b	0	0	43780.44	4+h7
0	1b	1b	0	0	1b	0	0	1b	43847.82	4+h7
0	0	1b	0	1b	0	0	1b	1b	43887.97	4+h10
1b	1b	0	0	1b	0	1b	0	0	43949.95	4+h10
0	0	1b	1b	0	0	1b	0	1b	43978.46	4+h10
0	1b	1b	0	0	1b	0	1b	0	44030.46	4+h10
1b	0	0	1b	0	1b	0	0	1b	44062.37	4+h10
0	1b	0	0	1b	1b	0	0	1b	44101.23	4+h10
0	1b	0	1b	0	0	1b	1b	0	44151.27	4+h10
1b	0	0	1b	1b	0	0	1b	0	44171.77	4+h10
1b	0	1b	0	0	1b	1b	0	0	44182.55	4+h10
0	1b	0	1b	0	1b	0	1b	0	44715.64	4+h13
1b	0	1b	0	1b	0	1b	0	0	44721.78	4+h13
0	1b	0	1b	0	1b	0	0	1b	44763.38	4+h13
1b	0	1b	0	1b	0	0	1b	0	44788.87	4+h13
0	1b	0	1b	0	0	1b	0	1b	44819.71	4+h13
1b	0	0	1b	0	1b	0	1b	0	44830.89	4+h13
1b	0	1b	0	0	1b	0	1b	0	44978.35	4+h13
0	0	1b	0	1b	0	1b	0	1b	45037.3	4+h13
0	1b	0	0	1b	0	1b	0	1b	45104.25	4+h13