u013250861

模型调参（二）：learning rate decay（学习率衰减）【使用库调整学习率：等间隔、多间隔、指数衰减、余弦退火函数、根据指标、自定义】【手动调整学习率】

一、学习率衰减的概念和必要性

解释①：如果在整个梯度下降过程中，保持learning rate不变，如果learning rate设置小了，会导致梯度下降过慢，如果设置大了，对于mini-batch来说最后就很难收敛，一直在最小值附近盘旋。所以动态改变learning rate很重要，在开始的时候，设置较大的learning rate，可以保证梯度下降的速度，慢慢减小，可以使最后的cost function在最小值非常小的范围内盘旋，得到一个比较满意的值。

解释②：学习率过大，在算法优化的前期会加速学习，使得模型更容易接近局部或全局最优解。但是在后期会有较大波动，甚至出现损失函数的值围绕最小值徘徊，波动很大，始终难以达到最优，如下图蓝色曲线所示。所以引入学习率衰减的概念，直白点说，就是在模型训练初期，会使用较大的学习率进行模型优化，随着迭代次数增加，学习率会逐渐进行减小，保证模型在训练后期不会有太大的波动，从而更加接近最优解，如下图中上面一条绿色曲线所示。

当学习率过大，以J(X)=X^2为例，学习率始终为1，梯度下降算法的运行过程：

可以看到无论进行多少轮迭代，参数始终在5和-5之间摇摆，而不是收敛到一个极小值。

二、什么是param_groups

optimizer通过param_group来管理参数组.param_group中保存了参数组及其对应的学习率,动量等等.所以我们可以通过更改param_group[‘lr’]的值来更改对应参数组的学习率。

例1：有两个`param_group`即,len(optim.param_groups)==2

optim.SGD([
                {'params': model.base.parameters()},
                {'params': model.classifier.parameters(), 'lr': 1e-3}
            ], lr=1e-2, momentum=0.9)

上面第一个例子中，我们分别为 model.base 和 model.classifier 的参数设置了不同的学习率，即此时 optimizer.param_grops 中有两个不同的param_group：

param_groups[0]: {‘params’: model.base.parameters()},
param_groups[1]: {‘params’: model.classifier.parameters(), ‘lr’: 1e-3}

每一个param_group都是一个字典，它们共同构成了param_groups，所以此时len(optimizer.param_grops)==2，

例2：一个参数组

optim.SGD(model.parameters(), lr=1e-2, momentum=.9)

手动调整学习率，通常可以定义如下函数：

def adjust_learning_rate(optimizer, epoch):
    """Sets the learning rate to the initial LR decayed by 10 every 30 epochs"""
    lr = args.lr * (0.1 ** (epoch // 30))
    for param_group in optimizer.param_groups:
        param_group['lr'] = lr

adjust_learning_rate() 函数就是通过for循环遍历取出每一个param_group，然后修改其中的键 ‘lr’ 的值，称之为手动调整学习率。

三、学习率衰减的类型【①使用库；②手动】

学习率衰减的类型有很多种，大致可以分为两类：

一是通过人为经验进行设定，如到达多少轮后，设定具体的学习率为多少；
二是使用库函数进行调整，随着迭代轮数的增加学习率自动发生衰减，这类有比较常用的指数型衰退，具体算法如下图

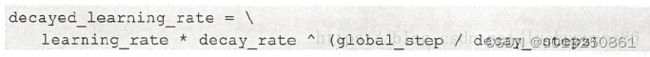
其中decayed_learning_rate为每一轮优化时使用的学习率，learning_rate为事先设定的初始学习率，decay_rate为衰减系数，decay_steps为衰减速度。

在tensorflow中指数型衰减通过调用tf.train.exponential_decay(learning_rate, global_step, decay_steps, decay_rate, staircase=False, name=None)实现。这里介绍一下decay_steps，若decay_steps=100，即表示100轮迭代后进行一次衰减，staircase=True时，global_step/decay_steps会被转化为整数，这使得学习率呈阶梯型下降（如下图黑色），若staircase=False，下图灰色为连续型衰减学习率。

1、使用库函数进行调整

Pytorch学习率调整策略通过 torch.optim.lr_sheduler 接口实现。pytorch提供的学习率调整策略分为三大类，分别是：

有序调整：等间隔调整(Step)，多间隔调整(MultiStep)，指数衰减(Exponential)，余弦退火(CosineAnnealing);
自适应调整：依训练状况伺机而变，通过监测某个指标的变化情况(loss、accuracy)，当该指标不怎么变化时，就是调整学习率的时机(ReduceLROnPlateau);
自定义调整：通过自定义关于epoch的lambda函数调整学习率(LambdaLR)。

在每个epoch的训练中，使用 scheduler.step() 语句进行学习率更新，此方法类似于optimizer.step()更新模型参数，即一次epoch对应一次scheduler.step()。但在mini-batch训练中，每个mini-bitch对应一个optimizer.step()。即用法如下：

optimizer = torch.optim.SGD(model.parameters(), lr=0.1)
scheduler = torch.optim.lr_scheduler.StepLR(optimizer, step_size=30, gamma=0.1)

def train(...):
    for i, data in enumerate(train_loader):
        ......
        y_ = model(x)
        loss = criterion(y_,y)
        loss.backward()
        optimizer.step()
        ......
 
for epoch in range(epochs):
    train(...)
    test(...)
    scheduler.step()

1.1 等间隔调整学习率 StepLR

torch.optim.lr_scheduler.StepLR(optimizer, step_size, gamma=0.1, last_epoch=-1)

每训练step_size个epoch，学习率调整为lr=lr*gamma.

以下内容中都将epoch和step对等，因为每个epoch中只进行一次scheduler.step()，实则该step指scheduler.step()中的step, 即step_size指scheduler.step()进行的次数。

参数：

optimizer: 神经网络训练中使用的优化器，如optimizer=torch.optim.SGD(…)
step_size(int): 学习率下降间隔数，单位是epoch，而不是iteration.
gamma(float): 学习率调整倍数，默认为0.1
last_epoch(int): 上一个epoch数，这个变量用来指示学习率是否需要调整。当last_epoch符合设定的间隔时，就会对学习率进行调整；当为-1时，学习率设置为初始值。

等间隔调整学习率：step_size=30, gamma=0.1

1.2 多间隔调整学习率 MultiStepLR

跟(1)类似，但学习率调整的间隔并不是相等的，如epoch=10时调整一次，epoch=30时调整一次，epoch=80时调整一次…

torch.optim.lr_sheduler.MultiStepLR(optimizer, milestones, gamma=0.1, last_epoch=-1)

参数：

milestone(list): 一个列表参数，表示多个学习率需要调整的epoch值，如milestones=[10, 30, 80].
optimizer: 神经网络训练中使用的优化器，如optimizer=torch.optim.SGD(…)
step_size(int): 学习率下降间隔数，单位是epoch，而不是iteration.
gamma(float): 学习率调整倍数，默认为0.1
last_epoch(int): 上一个epoch数，这个变量用来指示学习率是否需要调整。当last_epoch符合设定的间隔时，就会对学习率进行调整；当为-1时，学习率设置为初始值。

多间隔调整学习率：milestones=[10, 30, 80], gamma=0.1

1.3 指数衰减调整学习率 ExponentialLR

学习率呈指数型衰减，每训练一个epoch， $l r = l r g a m m a * e p o c h$ ，即 $lr×gamma^{epoch}$

torch.optim.lr_sheduler.ExponentialLR(optimizer, gamma, last_epoch)

参数：

gamma(float)：学习率调整倍数的底数，指数为epoch，初始值我lr, 倍数为 $gamma^{epoch}$
其它参数同上。

指数衰减调整学习率：gamma=0.9

1.4 余弦退火函数调整学习率

学习率呈余弦函数型衰减，并以 $2*T_{max}$ 为余弦函数周期，epoch=0对应余弦型学习率调整曲线的 $x = 0$ ， $y_{max}=lr$ ， $epoch=T_max$ 对应余弦型学习率调整曲线的 $x=\pi$ ， $y_{min}=eta_min$ 处，随着 $epoch>T_{max}$ ，学习率随epoch增加逐渐上升，整个走势同cos(x)。

torch.optim.lr_sheduler.CosineAnnealingLR(optimizer, T_max, eta_min=0, last_epoch=-1)

参数：

T_max(int): 学习率下降到最小值时的epoch数，即当epoch=T_max时，学习率下降到余弦函数最小值，当epoch>T_max时，学习率将增大；
eta_min: 学习率调整的最小值，即epoch=T_max时，lr_{min}=eta_min, 默认为0.
其它参数同上。

学习率余弦衰减：T_max=100

1.5 根据指标调整学习率 ReduceLROnPlateau

当某指标(loss或accuracy)在最近几个epoch中都没有变化(下降或升高超过给定阈值)时，调整学习率。

如当验证集的loss不再下降是，调整学习率；或监察验证集的accuracy不再升高时，调整学习率。

torch.optim.lr_sheduler.ReduceLROnPlateau(optimizer, mode='min', factor=0.1, patience=10,
										  verbose=False, threshold=0.0001, threshold_mode='rel', 
										  cooldown=0, min_lr=0, eps=1e-08)

参数：

mode(str): 模式选择，有min和max两种模式，min表示当指标不再降低(如监测loss)，max表示当指标不再升高(如监测accuracy)。
factor(float): 学习率调整倍数，同前面的gamma，当监测指标达到要求时，lr=lr×factor。
patience(int): 忍受该指标多少个epoch不变化，当忍无可忍时，调整学习率。
verbose(bool): 是否打印学习率信息，print( ‘Epoch {:5d} reducing learning rate of group {} to {:.4e}.’.format(epoch, i, new_lr), 默认为False, 即不打印该信息。
threshold_mode (str): 选择判断指标是否达最优的模式，有两种模式：rel 和 abs.
当threshold_mode == rel, 并且 mode == max时，dynamic_threshold = best * (1 + threshold);
当threshold_mode == rel, 并且 mode == min时，dynamic_threshold = best * (1 - threshold);
当threshold_mode == abs, 并且 mode == max时，dynamic_threshold = best + threshold;
当threshold_mode == abs, 并且 mode == min时，dynamic_threshold = best - threshold;
threshold(float): 配合threshold_mode使用。
cooldown(int): “冷却时间”，当调整学习率之后，让学习率调整策略冷静一下，让模型在训练一段时间，再重启监测模式。
min_lr(float or list): 学习率下限，可为float，或者list，当有多个参数组时，可用list进行设置。
eps(float): 学习率衰减的最小值，当学习率的变化值小于eps时，则不调整学习率。

optimizer = torch.optim.SGD(model.parameters(), args.lr,
 momentum=args.momentum, weight_decay=args.weight_decay)

scheduler = ReducelROnPlateau(optimizer,'min')
for epoch in range( args.start epoch, args.epochs ):
    train(train_loader , model, criterion, optimizer, epoch )
    result_avg, loss_val = validate(val_loader, model, criterion, epoch)
    # Note that step should be called after validate()
    scheduler.step(loss_val )

1.6 自定义调整学习率 LambdaLR

为不同参数组设定不同学习率调整策略。调整规则为：
lr = base_lr * lambda(self.last_epoch)
在fine-tune中特别有用，我们不仅可以为不同层设置不同的学习率，还可以为不同层设置不同的学习率调整策略。

torch.optim.lr_scheduler.LambdaLR(optimizer, lr_lambda, last_epoch=-1)

参数：

lr_lambda(function or list): 自定义计算学习率调整倍数的函数，通常时epoch的函数，当有多个参数组时，设为list.
其它参数同上。

例：

import torch.optim as optim

ignored_params = list(map(id, net.fc3.parameters()))
base_params = filter(lambda p: id(p) not in ignored_params, net.parameters())
optimizer = optim.SGD([
                            {'params': base_params},
                            {'params': net.fc3.parameters(), 'lr': 0.001 * 100}
                        ], lr=0.001, momentum=0.9, weight_decay=1e-4)
# Assuming optimizer has two groups.
lambda1 = lambda epoch: epoch // 3
lambda2 = lambda epoch: 0.95 ** epoch

scheduler = LambdaLR(optimizer, lr_lambda=[lambda1, lambda2])

for i in range(100):
    train(...)
    validate(...)
    scheduler.step()
    print('epoch: ', i, 'lr: ', scheduler.get_lr())

输出：

epoch: 0 lr: [0.0, 0.1]
epoch: 1 lr: [0.0, 0.095]
epoch: 2 lr: [0.0, 0.09025]
epoch: 3 lr: [0.001, 0.0857375]
epoch: 4 lr: [0.001, 0.081450625]
epoch: 5 lr: [0.001, 0.07737809374999999]
epoch: 6 lr: [0.002, 0.07350918906249998]
epoch: 7 lr: [0.002, 0.06983372960937498]
epoch: 8 lr: [0.002, 0.06634204312890622]
epoch: 9 lr: [0.003, 0.0630249409724609]

为什么第一个参数组的学习率会是 0 呢？来看看学习率是如何计算的。
第一个参数组的初始学习率设置为 0.001,
lambda1 = lambda epoch: epoch // 3,
第 1 个 epoch 时，由 lr = base_lr * lmbda(self.last_epoch)，
可知道 lr = 0.001 (0//3) ，又因为 1//3 等于 0，所以导致学习率为 0。
第二个参数组的学习率变化，就很容易看啦，初始为 0.1， lr = 0.1 * 0.95^epoch ，当
epoch 为 0 时， lr=0.1 ， epoch 为 1 时， lr=0.10.95。

附：给出画上述学习率变化图的程序：

# -*- coding:utf-8 -*-
'''本文件用于测试pytorch学习率调整策略'''

__author__ = 'puxitong from UESTC'

import torch
import torch.optim as optim
from torch.optim import lr_scheduler
from torchvision.models import AlexNet
import matplotlib.pyplot as plt 


model = AlexNet(num_classes=2)
optimizer = optim.SGD(params=model.parameters(), lr=0.1)

# 等间隔调整学习率，每训练step_size个epoch，lr*gamma
# scheduler = lr_scheduler.StepLR(optimizer, step_size=30, gamma=0.1)

# 多间隔调整学习率，每训练至milestones中的epoch，lr*gamma
# scheduler = lr_scheduler.MultiStepLR(optimizer, milestones=[10, 30, 80], gamma=0.1)

# 指数学习率衰减，lr*gamma**epoch
# scheduler = lr_scheduler.ExponentialLR(optimizer, gamma=0.9)

# 余弦退火学习率衰减，T_max表示半个周期，lr的初始值作为余弦函数0处的极大值逐渐开始下降，
# 在epoch=T_max时lr降至最小值，即pi/2处，然后进入后半个周期，lr增大
# scheduler = lr_scheduler.CosineAnnealingLR(optimizer, T_max=100, eta_min=0)

plt.figure()
x = list(range(100))
y = []
for epoch in range(100):
    scheduler.step()
    y.append(scheduler.get_lr()[0])

plt.plot(x, y)
plt.show()

2、手动调整学习率