周志华-机器学习（西瓜书） 集成学习 课后练习题8.3 Adaboost & 8.5 Bagging Python实现

scikit-learn及其安装

scikit-learn

scikit-learn是一个python的机器学习工具，可以进行简单高效的数据挖掘和数据分析，基于NumPy，SciPy和matplotlib构建。

功能	简介	应用举例
分类（Classification）	识别物体属于哪个类别	图像识别
回归 （Regression）	预测与对象关联的连续值属性	预测趋势
聚类（Clustering）	自动将相似对象归为一组	分组实验结果
降维（Dimensionality reduction）	减少要考虑的随机变量的数量	可视化
模型选择（Model selection）	比较，验证和选择参数和模型	提高准确性
预处理（Preprocessing）	特征提取和归一化	转换输入数据

安装

本文中的安装主要是基于PyCharm，如果不是的话建议在网上寻找相对应的安装方法，在这里就不再赘述。

1. 点击File(文件)菜单，在下拉菜单中选择settings(设置)
   

2. 其次，在project interpreter(项目解释器)中点击“+”号
   

3. 在搜索框中输入所要添加的第三方库的名称，如NumPy，然后在左下角点击第一个选项Install Package。
   

4. 安装完成之后就会有提示。
   

5. 等到安装好下面所示的这些库之后关闭重启即可。
   

6. 下面是前置清单：

   • Python (>= 3.5)
   • NumPy (>= 1.11.0)
   • SciPy (>= 0.17.0)
   • joblib (>= 0.11)
   • Matplotlib版本（>=1.5.1）
   • scikit-image（> = 0.12.3）
   • pandas（> = 0.18.0）

集成学习

一、利用sklearn库进行分析

直接上代码：

import numpy as np
import matplotlib.pyplot as plt
from sklearn.ensemble import BaggingClassifier, AdaBoostClassifier
from sklearn.tree import DecisionTreeClassifier

# 西瓜数据集3.0a
D = np.array([
    [1, 1, 1, 1, 1, 1, 0.697, 0.460, 1],
    [2, 1, 2, 1, 1, 1, 0.774, 0.376, 1],
    [2, 1, 1, 1, 1, 1, 0.634, 0.264, 1],
    [1, 1, 2, 1, 1, 1, 0.608, 0.318, 1],
    [3, 1, 1, 1, 1, 1, 0.556, 0.215, 1],
    [1, 2, 1, 1, 2, 2, 0.403, 0.237, 1],
    [2, 2, 1, 2, 2, 2, 0.481, 0.149, 1],
    [2, 2, 1, 1, 2, 1, 0.437, 0.211, 1],
    [2, 2, 2, 2, 2, 1, 0.666, 0.091, 0],
    [1, 3, 3, 1, 3, 2, 0.243, 0.267, 0],
    [3, 3, 3, 3, 3, 1, 0.245, 0.057, 0],
    [3, 1, 1, 3, 3, 2, 0.343, 0.099, 0],
    [1, 2, 1, 2, 1, 1, 0.639, 0.161, 0],
    [3, 2, 2, 2, 1, 1, 0.657, 0.198, 0],
    [2, 2, 1, 1, 2, 2, 0.360, 0.370, 0],
    [3, 1, 1, 3, 3, 1, 0.593, 0.042, 0],
    [1, 1, 2, 2, 2, 1, 0.719, 0.103, 0]])
# 将特征与标签分离，得到数据集
train_d, label_d = D[:, [-3, -2]], D[:, -1]

# max_depth限定决策树是否为决策树桩，n_estimator表示不同数量的基学习器集成，下面以Bagging为例，AdaBoost同理
clf1 = BaggingClassifier(DecisionTreeClassifier(max_depth=1), n_estimators=3)
clf2 = BaggingClassifier(DecisionTreeClassifier(max_depth=1), n_estimators=5)
clf3 = BaggingClassifier(DecisionTreeClassifier(max_depth=1), n_estimators=11)
# 分别进行学习
for clf in [clf1, clf2, clf3]:
    clf.fit(train_d, label_d)

x_min, x_max = train_d[:, 0].min() - 1, train_d[:, 0].max() + 1
y_min, y_max = train_d[:, 1].min() - 1, train_d[:, 1].max() + 1
# 生成网格点坐标矩阵
xset, yset = np.meshgrid(np.arange(x_min, x_max, 0.02), np.arange(y_min, y_max, 0.02))
clf_set, label_set = [clf1, clf2, clf3], []
# 进行预测，预测完了之后添加到标签集中
for clf in clf_set:
    out_label = clf.predict(np.c_[xset.ravel(), yset.ravel()])
    out_label = out_label.reshape(xset.shape)
    label_set.append(out_label)

# 生成图像
fig, axes = plt.subplots(nrows=1, ncols=3, figsize=(12, 4))
(ax0, ax1, ax2) = axes.flatten()
for k, ax in enumerate((ax0, ax1, ax2)):
    ax.contourf(xset, yset, label_set[k], cmap=plt.cm.Set3)
    for i, n, c in zip([0, 1], ['bad', 'good'], ['black', 'red']):
        idx = np.where(label_d == i)
        ax.scatter(train_d[idx, 0], train_d[idx, 1], c=c, label=n)
    ax.set_xlim(0, 1)
    ax.set_ylim(0, 0.6)
    ax.legend(loc='upper left')
    ax.set_ylabel('sugar')
    ax.set_xlabel('densty')
    ax.set_title('decision boundary for %s' % (k + 1))
plt.show()

8.3

从网上下载或自己编程实现AdaBoost，以不剪枝决策树为基学习器，在西瓜数据集3.0a上训练一个AdaBoost集成，并与图8.4进行比较。

简单来说Adaboost得到的是一个加法模型，他通过迭代计算一个一个的分类器，然后以一定的权值相加在一起，得到一个总的模型。因为每一个单独的分类器，都依靠上一次的训练结果在进行这一次的训练，所以这就是所谓的串行训练。

Adaboost实际上每学到一个学习器，用错误率做了两件事：

• 根据当前训练所得分类器的错误率得到当前分类器在总分类器中的权值。当前分类器的正确率越高，此权值就越大。
• 根据错误率修改当前样本的权值分布。初始每个数据的权值都是一样的，当前分类器误分的数据将会得到更大的权值，目的是在下一个分类器的训练中，重点关注之前容易被误分的数据，减少错误率。

如果完全按照题目所说，以不剪枝决策树为基学习器，则基本上训练后的每个决策树分类器都是趋于一致。因为第一颗树错误率就为0了，样本权重也不会发生改变，直接生成了一个完美符合数据的决策树，此时AdaBoost就没意义了。

下图即是使用不剪枝决策树作为基学习器，在基学习器数量1时的分类边界：（随着基学习器数量增加，也不会有任何变化，因为已经完美符合数据了）

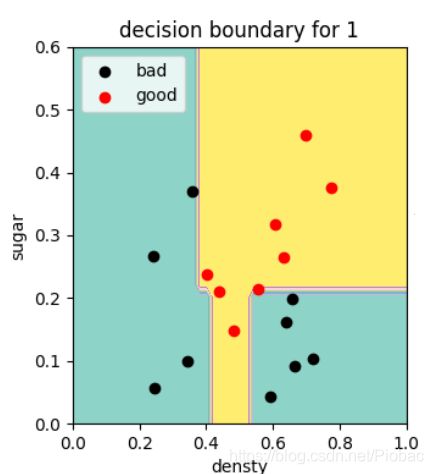
如果要保证个体学习器的多样性，应采用单层决策树作为基学习器，即以决策树桩作为弱学习器。

这里代码是限定树的深度为2，但训练到第四颗树，错误率就已经到0了，下图给出来的决策边界，其实基本上就是第四颗树的决策了，因为错误率为0，权重已经不再改变了。

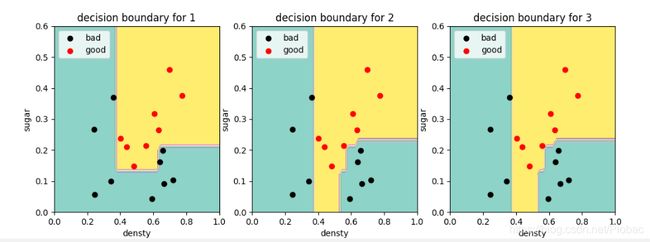
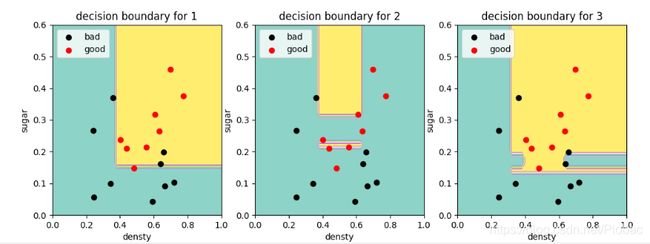
而书上的图8.4，在基学习器数量为11时明显比5效果好很多，所以我们再把树的深度限定为1进行尝试，下面是基学习器数量分别为1、2、3时的决策边界：

图8.4：

分析结果：对比可见，当AdaBoost集成数量增加时，决策边界总体上趋于复杂，同时分类错误率降低。

8.5

试编程实现Bagging，以决策树桩为基学习器，在西瓜数据集3.0a上训练一个Bagging集成，并与图8.6进行比较。

首先，我们还是先利用sklearn库进行分析。

当我们设置决策树最大深度为1时，则无论集成学习器数量增加多少，最终错误率仍然很高。

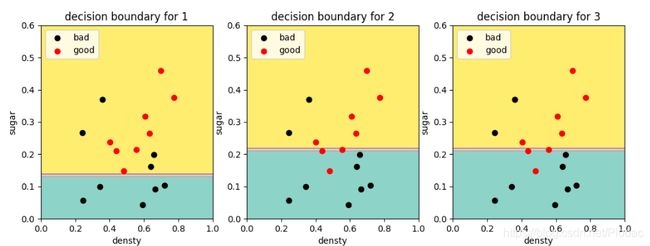
而当决策树最大深度为2时，总体上随基学习器的数量增加，分类错误率降低，这与图8.6的情况基本一致。

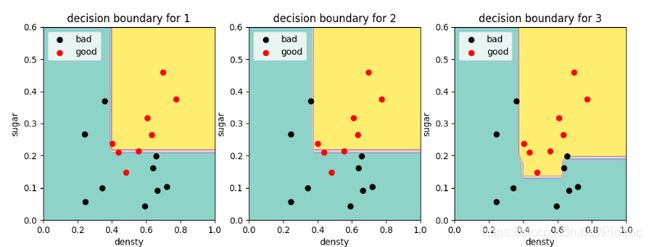
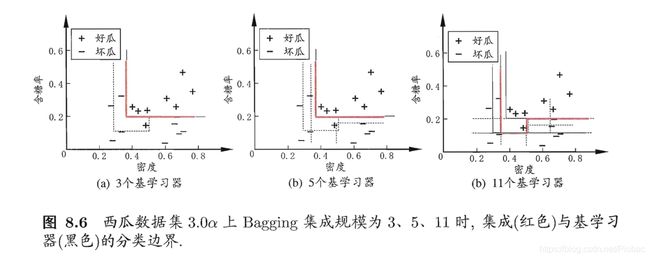
这是因为：Boosting算法的基学习器通常是弱学习器，特点是偏差较大，通过Boosting算法可以逐步提升，较低偏差；而Bagging的基学习器通常是强学习器，比如，全决策树和神经网络，特点是偏差较小，但是容易过拟合，方差较大，通过多个基学习器的平均来减小方差，防止过拟合。

而这里采用的基学习器是决策树桩，本身偏差较大，Bagging集成只有降低方差的效果，对于偏差并无改善，所以集成后的训练误差仍然很低。

如果我们采用全决策树，当基学习器增加时，就得到了非常精准并且复杂的决策边界：

二、8.5编程实现

代码：

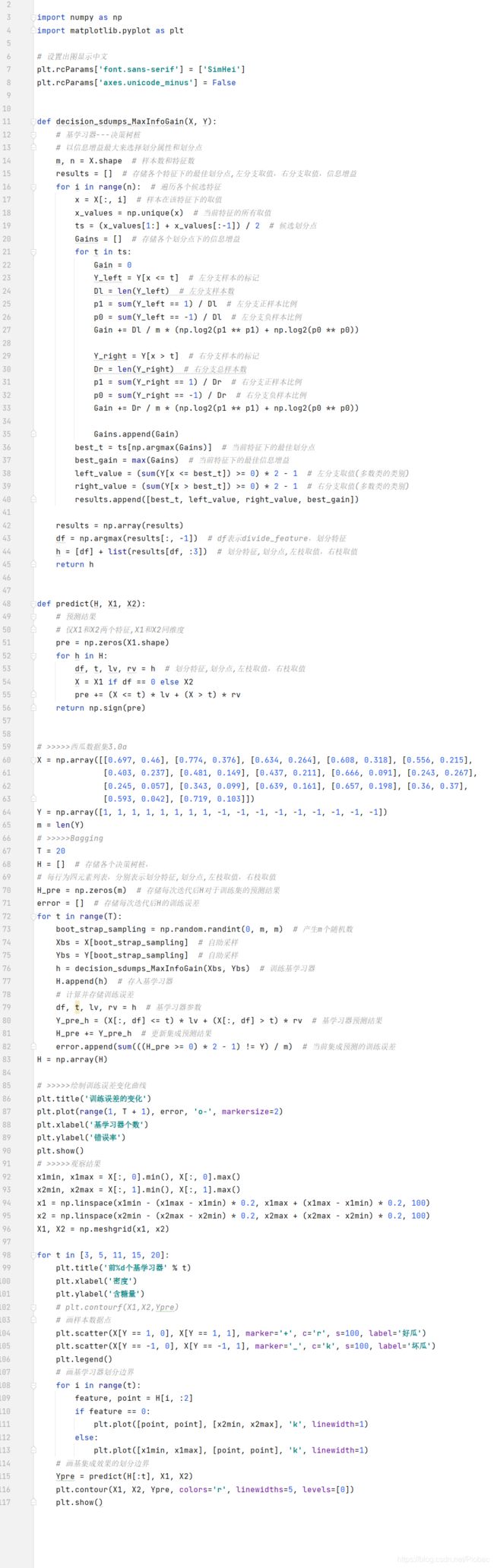
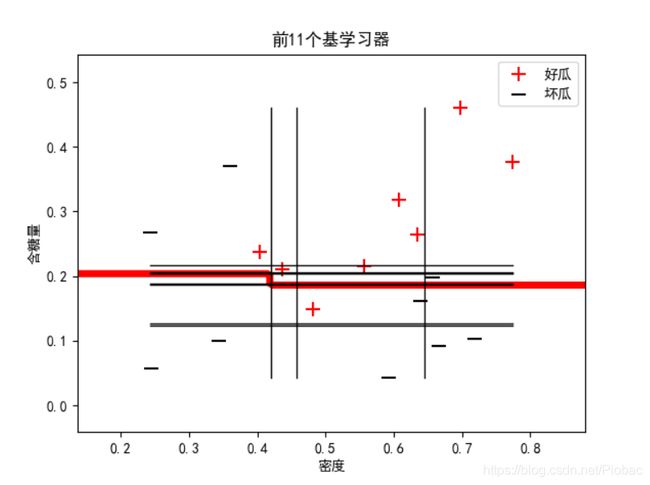
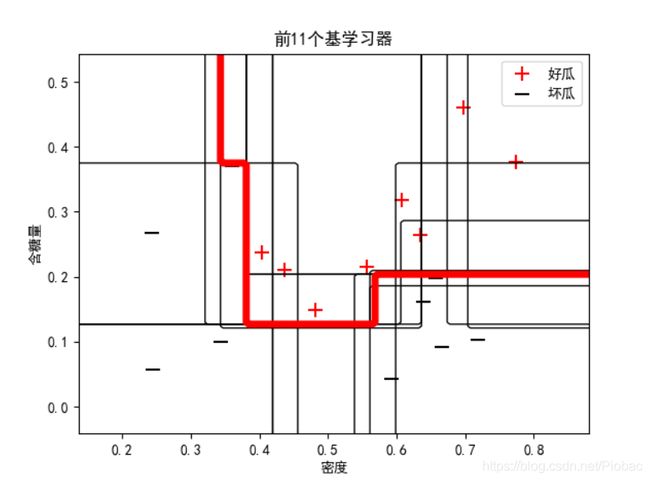
上面的代码中，我们以决策树桩为基学习器，下图是某一次的运算结果：

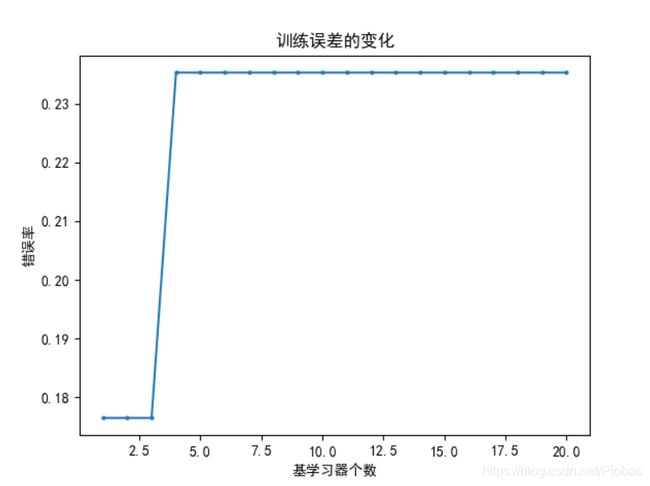
和我们在上面分析的一样，因为bagging集成只有降低方差的效果，对于偏差并无改善，所以集成后的训练误差仍然很低。这也就造成了我们在增加基学习器的前提下，准确率甚至降低的情况。（实际上是一直稳定的低。）
可以从下面的三个图中看出：

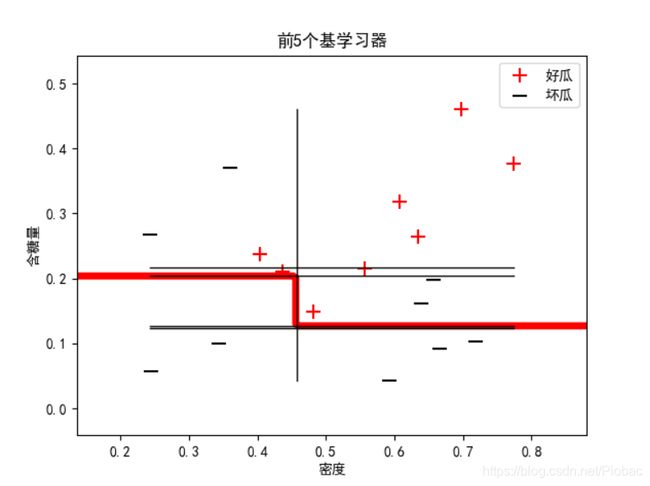
而在我们借助sklearn把基学习器改为全决策树来集成时，情况迅速得到了改善。下图是某次运算结果：

可见，前4个集成后便已经实现了零训练误差。



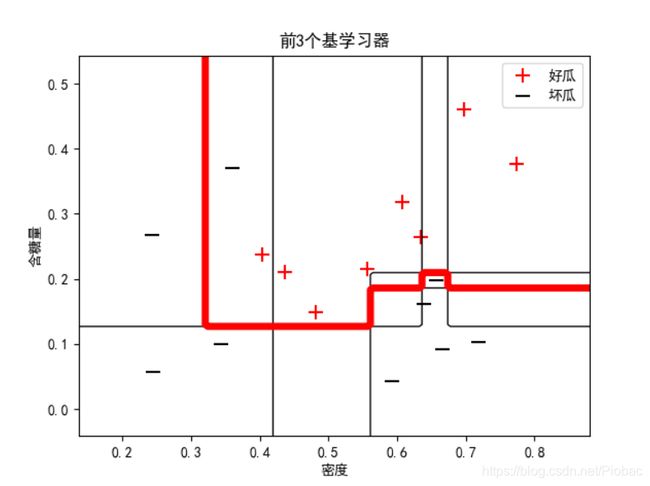
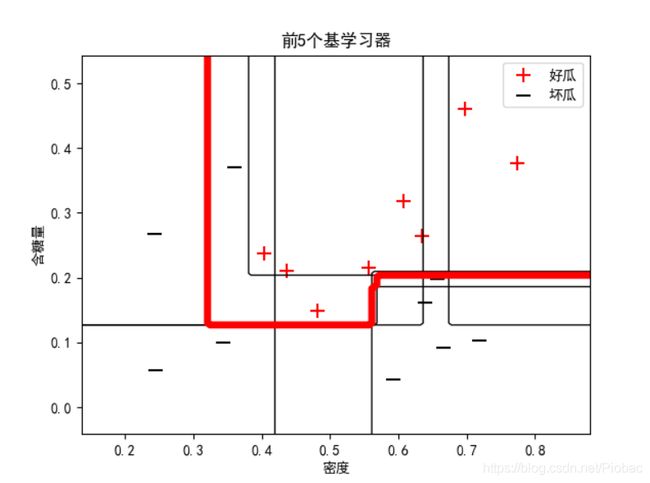
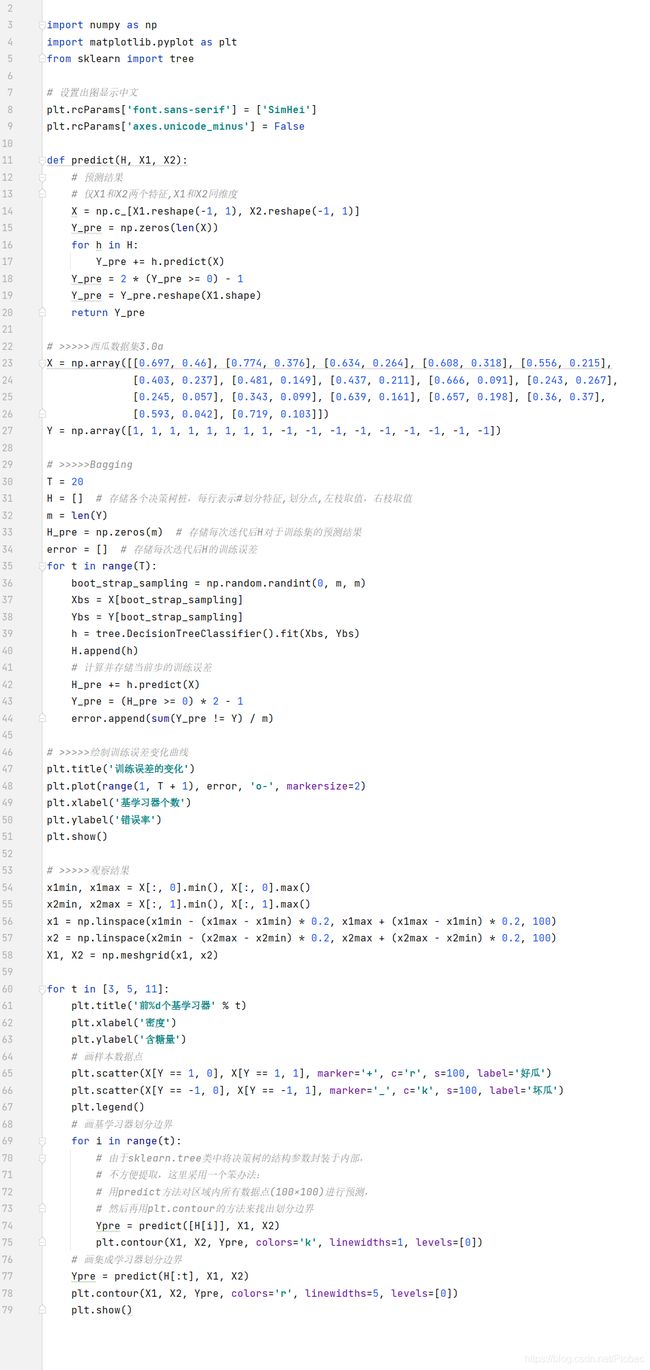
下面是改用全决策树的bagging集成代码：

引用

本文参考了多篇文章，非常感谢这些作者在我学习过程中给予的帮助，我将在下面给出所有文章的链接。
再次感谢他们，如果没有他们的帮助，我的学习过程将会变得万分艰难。

1. Bagging 简述
2. scikit-learn安装步骤
3. 机器学习（周志华）课后习题——第八章——集成学习
4. 机器学习-周志华-个人练习8.3和8.5
5. 西瓜书课后题8.3(Adaboost))