SE(Squeeze and Excitation)模块的理解以及代码实现

1. 简介

SE Block并非一个完整的网络，而且一个子结构，可以嵌在其他分类或检测模型中。SE Block的核心思想是通过网络根据loss去学习特征权重，使得有效的feature map权重更大，无效或效果小的feature map权重更小的方式去训练模型已达到更好的结果。

当然，SE block嵌在原有的一些分类网络中不可避免地增加了一些参数和计算量，但是在效果面前还是可以接受的。

2. 运算讲解

SE block示意图：

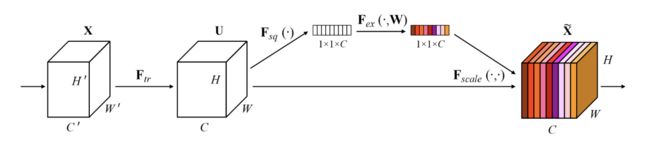
Step1： 卷积操作(即图中的$F_{tr}$操作)
严格来讲这一步是转换操作，并不是SE block的一部分，就是一个标准的卷积操作。输入输出定义如下：
$$F_{tr}：X\to U,X\in R^{W^{\prime }\ast H^{\prime }\ast C^{\prime }},U\in R^{W\ast H\ast W}$$
计算公式就是常规的卷积操作，计算公式如下：
$$u_c=v_c\ast X=\sum _{s=1}^{C^{\prime }}{v}_c^s\ast x^s$$
其中，$v_c$ 表示第c个卷积核， $x^s$ 表示当前卷积核覆盖下的第s个输入， $C^{\prime }$ 表示卷积核个数。

该操作得到了上图中左起第2个矩阵，其维度 = [H ,W, C]

Step2: $F_{sq}$操作（即Squeenze操作）
该操作就是一个：global average pooling操作，公式如下：
$$z_c=F_{sq}(u_c)=\frac{1}{W\ast H}\sum _{i=1}^W\sum _{j=1}^H{u}_c(i,j)$$

这里使用代码进行一定的解释：
代码如下：

x = torch.ones(size=(1, 2, 2, 3))
x[0][0][0][0] = 7
print("x = ", x)

avg_pool = torch.nn.AdaptiveAvgPool2d(1)    # 全局平均池化
x_pool = avg_pool(x)
print("x_pool.shape = ", x_pool.shape)
print("x_pool = ", x_pool)

输出结果：

计算的是每个通道的平均值，输出的shape=[1, 2, 1, 1]

这一步的结果相当于表明该层C个通道的数值分布情况，或者叫全局信息。

Step3: $F_{ex}$操作（即Excitation操作）
计算公式如下：
$$s=sigmoid(W_2\ast Relu(W_{1}z))$$
其中的$z$表示上一步的$z$, $W_1,W_2$ 表示的是线性层。这里计算出来的$s$就是该模块的核心，用来表示各个channel的权重， 而且这个权重是通过前面这些全连接层和非线性层学习得到的，因此可以end-to-end训练。这两个全连接层的作用就是融合各通道的feature map信息，因为前面的squeeze都是在某个channel的feature map里面操作。

这里结合代码容易理解（即Pytorch实现SE模块）：

class SELayer_2d(nn.Module):
    def __init__(self, channel, reduction=16):
        super(SELayer_2d, self).__init__()
        self.avg_pool = torch.nn.AdaptiveAvgPool2d(1)
        self.linear1 = nn.Sequential(
            nn.Linear(channel, channel // reduction, bias=False),
            nn.ReLU(inplace=True)
        )
        self.linear2 = nn.Sequential(
            nn.Linear(channel // reduction, channel, bias=False),
            nn.Sigmoid()
        )


    def forward(self, X_input):
        b, c, _, _ = X_input.size()  	# shape = [32, 64, 2000, 80]
        
        y = self.avg_pool(X_input)		# shape = [32, 64, 1, 1]
        y = y.view(b, c)				# shape = [32,64]
        
        # 第1个线性层（含激活函数），即公式中的W1，其维度是[channel, channer/16], 其中16是默认的
        y = self.linear1(y)				# shape = [32, 64] * [64, 4] = [32, 4]
        
        # 第2个线性层（含激活函数），即公式中的W2，其维度是[channel/16, channer], 其中16是默认的
        y = self.linear2(y) 			# shape = [32, 4] * [4, 64] = [32, 64]
        y = y.view(b, c, 1, 1)			# shape = [32, 64, 1, 1]， 这个就表示上面公式的s, 即每个通道的权重

        return X_input*y.expand_as(X_input)

测试代码：

    data = torch.ones((32, 64, 2000, 80))
    se_2d = SELayer_2d(64)
    data_out = se_2d.forward(data)
    print("data_out = ", data_out.shape)

Step4: $F_{scale}$操作
计算公式如下：
$$x=F_{scale}(u_c,s_c)=s_c\cdot u_c$$

其中，$u_c$表示$u$中的一个通道，$s_c$表示通道的权重。因此，相当于把每个通道的值乘以其权重。

代码即上述代码中的最后一行：

# y.expand_as(X_input)表示将y扩张到和X_input一样的维度
X_input*y.expand_as(X_input)		# 每个通道的值，乘以对应的权重

附录：
论文：Squeeze-and-Excitation Networks
论文链接：https://arxiv.org/abs/1709.01507
代码地址：https://github.com/hujie-frank/SENet
PyTorch代码地址：https://github.com/miraclewkf/SENet-PyTorch

引用：
有参考添加链接描述，在此文章的理解上，增加了一些代码注释。