数据结构——C++(未完)
系列文章目录
提示:这里可以添加系列文章的所有文章的目录,目录需要自己手动添加
例如:第一章 Python 机器学习入门之pandas的使用
提示:写完文章后,目录可以自动生成,如何生成可参考右边的帮助文档
文章目录
- 系列文章目录
- 前言
- 一、线性表
-
- 1.线性表的顺序存储结构
- 2.线性表的链式存储结构——单链表
- 3.线性表的链式存储结构——循环链表
- 3.线性表的链式存储结构——双向链表
- 二、栈
-
- 1.顺序栈
- 2.链栈
- 三、队列
-
- 1.顺序—循环队列
- 2.链队列
- 四、串
- 总结
前言
提示:这里可以添加本文要记录的大概内容:
例如:随着人工智能的不断发展,机器学习这门技术也越来越重要,很多人都开启了学习机器学习,本文就介绍了机器学习的基础内容。
一、线性表
1.线性表的顺序存储结构
线性表的顺序存储结构是指在内存中用一组地址连续的存储空间顺序存放线性表的各数据元素,使得逻辑关系上相邻的数据元素在物理位置上也相邻。
若线性表的每个元素占用d个存储单元,则表中和第 i i i个元素的存储位置 L o c ( a i ) Loc(a_{i}) Loc(ai) 满足如下关系式: L o c ( a i ) = L o c ( a 1 ) + ( i − 1 ) ∗ l Loc(a_{i})=Loc(a_1)+(i-1)*l Loc(ai)=Loc(a1)+(i−1)∗l
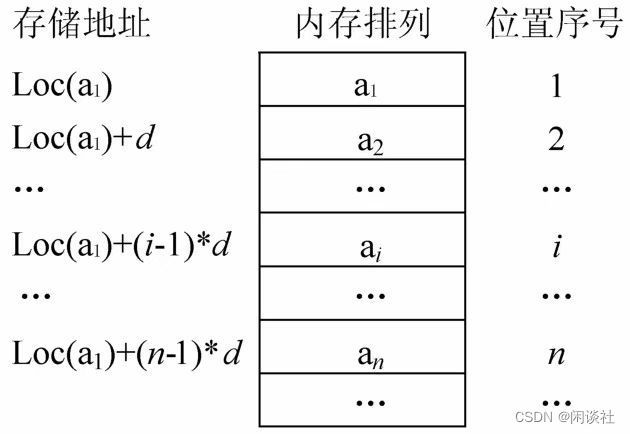
也就是说,只要知道顺序表的首地址和每个数据元素所占用地址单元的个数,就可以求出第i个数据元素的地址。
定义如下顺序表的数据结构类型:
typedef int DataType;
const int MAXSIZE = 20;
class SequenList {
//数据元素a1,a2,a3,……,an;对应的索引是data[0],data[1],data[2],……,data[n-1]
public:
void Initiate(); //初始化
int Length();
int Insert(DataType x, int i);//在位置i处前插入值x
int Deleted(int i);
int Locate(DataType x); //寻找数据元素x的位置
DataType Get(int i);
void print();
private:
DataType data[MAXSIZE] = {1,2,3,4,5,6,7,8,9};
int len=9;
};
具体算法实现如下
void SequenList::Initiate() {
//初始化
len = 0;
}
int SequenList::Insert(DataType x, int i) {
//在第i个数据元素前插入一个新的数据元素x
//将第i个到第len个元素往后移动一个位置,空出的位置插入新的元素x
//表长度加1
int j;
if (len >= MAXSIZE) {
cout << "数据溢出" << endl;
return 0;
}
else if (( i < 1 ) ||( i > len + 1)) {
cout << "插入位置不合法" << endl;
return 0;
}
else {
for (j = len; j >= i; --j) {
data[j] = data[j - 1]; //元素后移
}
data[i-1] = x; //在第i个数据元素前插入元素
++len; //表长度加一
return 1;
}
}
int SequenList::Deleted(int i) {
//删除第i个位置上的元素
//表长度减1
int j;
if ((i < 1) || (i > len)) {
cout << "删除位置不合法" << endl;
return 0;
}
else {
for (j = i; j < len; ++j) {
data[j - 1] = data[j];
}
--len;
return 1;
}
}
int SequenList::Locate(DataType x) {
//寻找数据元素x的位置
int j=0;
while ((j < len) && (data[j] != x))
++j;
if (j < len)
return j + 1;
else
return 0;
}
int SequenList::Get(int i) {
//读取第i个元素的值
if ((i < 1) || (i > len)) {
cout << "读取位置不合法" << endl;
return NULL;
}
else
return data[i - 1];
}
int SequenList::Length() {
return len;
}
void SequenList::print() {
for (auto c : data) {
cout << c << " ";
}
cout << endl;
}
int main()
{
SequenList S;
S.Insert(10, 2);
S.print();
int position=S.Locate(3);
cout << position << endl;
system("pause");
return 0;
}
2.线性表的链式存储结构——单链表
由于对顺序表进行插入、删除、移动等操作时需要移动数据来实现,严重影响了效率。链式存储结构不要求逻辑上相邻的元素在物理位置上也相邻,而是通过链建立数据元素之间的逻辑关系。
对每个数据元素 a i a_i ai,除了存放自身的数据信息外(数据域),还需要存放其后继 a i + 1 a_{i+1} ai+1所在存储单元的地址(指针域)。这两部分信息构成“结点”。
由于每个结点中只有一个指向后继的指针,此类又叫做“单链表”。

整个链表的存取必须从头指针开始,头指针指示链表第一个结点的存储位置。同时由于最后一个数据元素没有直接后继,因此最后一个结点的指针为NULL
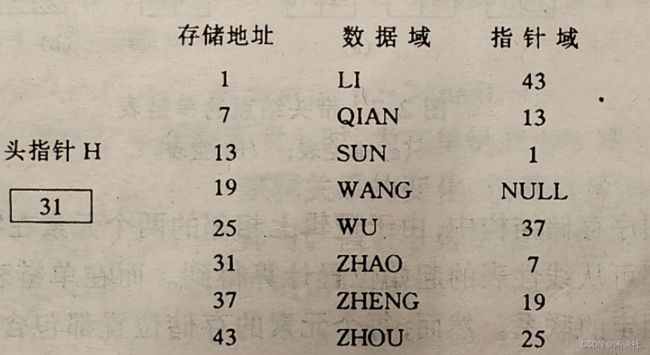
链表与顺序表不同,它是一种动态管理的存储结构,链表中的每个结点占用的存储空间不是预先分配的,而是在运行时系统根据需求动态生成的,因此建立单链表应该从空表开始。
另外,为了方便,一般也在链表中设置头结点。如下图:
这么做的好处是:
1.便于首元结点( a 1 a_1 a1)的处理
首元结点的地址保存在头结点的指针域中,所以链表的第一个位置上的操作和其他位置一致,无需进行特殊处理
2.便于空表和非空表的统一处理
无论链表是否为空,头指针都是指向头结点的非空指针,因此处理也就统一了。

定义如下链表的数据结构类型:
typedef int DataType;
class Item {
public:
DataType data;
Item* next;
Item() = default;
Item(int x ):data(x),next(nullptr){}
Item(int x,Item* next):data(x),next(next){}
};
class Link {
public:
Item* head; //链表头指针
Link() { head = NULL; } //构造函数
~Link() { DeleteAll(); } //析构函数
void Initiate(); //初始化
void DeleteAll(); //删除所有结点
void HeadCreateWithHead(int n); //从头建立带表头的链表
void TailCreateWithHead(int n); //从尾建立带表头的链表
int Length(); //求链表长度
Item* LocateX(DataType x); //查找值为x的元素
Item* LocateI(int i); //查找第i个元素
DataType Get(int i); //取第i个元素
bool InsertHead(DataType x, int i);//在第i个结点前插入x
bool InsertTail(DataType x, int i);//在第i个结点后插入x
bool Deleted(int i); //删除第i个结点
void Print();
};
具体算法如下
void Link::Initiate() {
DeleteAll();
head = NULL;
}
void Link::DeleteAll() {
Item* p = head, * q;
while (p != NULL) {
q = p->next;
delete p;
p = q;
}
head = NULL;
}
void Link::HeadCreateWithHead(int n) {
DeleteAll();
Item* p, * s;
p = new Item();//给头指针分配内存
p->next = NULL;//初始时刻头指针为空
for (int i = 1; i <= n; ++i) {
s = new Item();
cin >> s->data;
s->next = p->next;
p->next = s;
}
head = p;
}
void Link::TailCreateWithHead(int n) {
DeleteAll();
Item* p, * s, * r;
p = new Item();
p->next = NULL;
r = p;
for (int i = 1; i <= n; ++i) {
s = new Item();
cin >> s->data;
r->next = s;
r = s; //令r也指向s
}
r->next = NULL;
head = p;
}
int Link::Length() {
Item* p;
p = head->next;
int j = 0;
while (p != NULL) {
++j;
p = p->next;
}
return j;
}
Item* Link::LocateX(DataType x) {
//返回该节点的指针
Item* p;
p = head->next;
while ((p != NULL) && (p->data != x))
p = p->next;
if (p)
return p;
else {
cout << x << "不存在此链表中" << endl;
return NULL;
}
}
Item* Link::LocateI(int i) {
//返回该节点的指针
Item* p;
int j = 1;
p = head->next;
if (i == 0) return head;
while ((p != NULL) && (j < i)) {
p = p->next;
++j;
}
if (j==i)
return p;
else {
cout << "位置错误" << endl;
return NULL;
}
}
DataType Link::Get(int i) {
Item* p;
p = head->next;
int j = 1;
while ((j < i) && (p != NULL)) {
++j;
p = p->next;
}
if ((p == NULL) || (j > i)) {
cout << "位置错误" << endl;
return NULL;
}
else
{
return p->data;
}
}
bool Link::InsertHead(DataType x, int i) {
Item* p, * s;
p = LocateI(i - 1);
if (p == NULL) {
cout << "位置错误" << endl;
return NULL;
}
s = new Item();
s->data = x;
s->next = p->next;
p->next = s;
return true;
}
bool Link::InsertTail(DataType x, int i) {
Item* p, * s;
p = LocateI(i);
if (p == NULL) {
cout << "位置错误" << endl;
return NULL;
}
s = new Item();
s->data = x;
s->next = p->next;
p->next = s;
return true;
}
bool Link::Deleted(int i) {
Item* p,*q;
p = LocateI(i - 1);
if (p == NULL) {
cout << "位置错误" << endl;
return false;
}
q = p->next;
if (q != NULL) {
p->next = q->next;
delete q;
return true;
}
else {
cout << "位置错误" << endl;
return false;
}
}
void Link::Print() {
Item* p;
p = head->next;
while (p != NULL) {
cout << p->data << " ";
p = p->next;
}
cout << endl;
}
int main()
{
Link L;
L.TailCreateWithHead(5);
L.Print();
system("pause");
return 0;
}
3.线性表的链式存储结构——循环链表
对于单链表而言,最后一个结点的指针域是空指针。如果将该链表头指针置入该指针域,则使得链表头尾结点相连,就构成了循环单链表。

对两个循环单链表H1、H2的连接操作,是将H2的第一个数据结点接到H1的尾结点。如用头指针标识,则需要找到第一个链表的尾结点,其时间复杂度为O(n);而链表若用尾指针R1、R2标识,则时间复杂度为O(1)。操作如下:
p= R1->next; //保存R1的头结点指针
R1->next=R2->next->next; //头尾连接
delete R2->next; //释放第二个表的头结点
R2->next=p; //组成循环链表
3.线性表的链式存储结构——双向链表
在每个结点前加一个指向前驱的指针域,即为双向链表
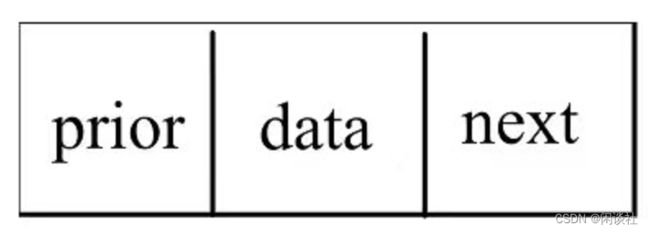
1,插入操作
① s->prior=p->prior;
② p->prior->next=s;
③ s->next=p;
④ p->prior=s;
2,删除操作
① p->prior->next=p->next;
② p->next->prior=p->prior;
delete p;
二、栈
- 栈是限制在表的一端进行插入和删除的线性表。
- 表中允许插入、删除的这一端称为栈顶,栈顶的当前位置是动态变化的;
- 不允许插入和删除的另一端称为栈底,栈底是固定不变的。
- 当表中没有元素时称为空栈。
- 栈的插入运算称为进栈、压栈或入栈,栈的删除运算称为退栈或出栈。
- 进栈的顺序是e1、e2、e3,出栈的顺序为e3、e2、e1,所以栈又称为后进先出线性表(Last In First Out),简称LIFO表,或称先进后出线性表。其特点是先进后出或者后进先出。
1.顺序栈
顾名思义,利用顺序存储方式实现的栈称为顺序栈。
类似于顺序表的定义,要分配一块连续的存储空间存放栈中的元素,栈底位置可以固定地设置在数组的任何一端(一般在下标为0的一端),而栈顶是随着插入和删除而变化的,再用一个变量指明当前栈顶的位置(实际上是栈顶元素的下一个位置)。
typedef int DataType;
class SeqStack {
private:
DataType* base;//栈底指针
DataType* top;//栈顶指针,始终指向栈顶元素的最后一个位置
int size;//栈的大小
public:
SeqStack(int stacksize = 100) {
base = new DataType[stacksize];
top = base;
size = stacksize;
}
~SeqStack() {
delete[] base;
top =NULL;
base = NULL;
}
int Empty_Stack(); //判断栈是否为空
int Push_Stack(DataType e); //将元素e插入栈顶
int Pop_Stack(DataType& e); //从栈顶删除一个元素到e中返回
int GetTop_Stack(DataType& e); //从栈顶取出一个元素到e中返回
void Print();
};
int SeqStack::Empty_Stack() {
return ((top <= base)); //top≤base为空栈,返回1
}
int SeqStack::Push_Stack(DataType e) {
if ((top - base) < size) { //判断是否满栈
*top = e;
++top;
return 1;
}
else
{
return 0;
}
}
int SeqStack::Pop_Stack(DataType& e) {
if (top > base) { //判断栈是否为空
--top; //栈顶top指向的是栈顶元素的后一位置
e = *top;
return 1;
}
else
return 0;
}
int SeqStack::GetTop_Stack(DataType& e) {
if (top > base) { //判断栈是否为空
e = *(top-1);//栈顶top指向的是栈顶元素的后一位置
return 1;
}
else
return 0;
}
void SeqStack::Print() {
int i = 0;
while ((top-i)>base ) {
cout << *(top-1-i) << " ";
++i;
}
}
int main()
{
SeqStack S;
S.Push_Stack(1);
S.Push_Stack(2);
S.Push_Stack(3);
S.Push_Stack(4);
S.Print();
system("pause");
return 0;
}
2.链栈
一般链栈用单链表表示。
因为链栈中的主要运算是在栈顶进行插入和删除操作,显然在单链表的表头插入和删除都比较方便,因此以头指针作为栈顶,而且没有必要像单链表那样为了运算方便而附加一个头结点。

typedef int DataType;
class StackNode {
public:
DataType data;
StackNode* next;
StackNode() = default;
StackNode(int x) :data(x), next(nullptr) {}
StackNode(int x, StackNode* next) :data(x), next(next) {}
};
class LinkStack {
private:
StackNode* top;
public:
LinkStack() {
top = NULL;
}
~LinkStack() {
StackNode* p;
while (top) {
p = top;
top = top->next;
delete p;
}
top = NULL;
}
int Empty_Stack(); //判断是否为空栈
int Push_Stack(DataType e);//将元素e插入栈顶
int Pop_Stack(DataType& e);//从栈顶删除一个元素到e中返回
int GetTop_Stack(DataType& e);//从栈顶取出一个元素到e中返回
void Print();
};
int LinkStack::Empty_Stack() {
return (!top);
}
int LinkStack::Push_Stack(DataType e) {
//入栈操作是在栈的顶部进行插入操作,相当于在单链表的表头(第一个元素之前)插入一个新元素。
StackNode* p = new StackNode();
if (p) {
p->data = e;
p->next = top;
top = p;
return 1;
}
else
{
return 0;
}
}
int LinkStack::Pop_Stack(DataType& e) {
StackNode* p;
if (top) {
p = top;
e = p->data;
top = top->next;
delete p;
return 1;
}
else
{
return 0;
}
}
int LinkStack::GetTop_Stack(DataType& e) {
if (top) {
e = top->data;
return 1;
}
else
{
return 0;
}
}
void LinkStack::Print() {
StackNode* p;
p = top;
while (p) {
cout << p->data << " ";
p = p->next;
}
}
int main()
{
LinkStack L;
L.Push_Stack(1);
L.Push_Stack(2);
L.Push_Stack(3);
L.Push_Stack(4);
L.Print();
system("pause");
return 0;
}
三、队列
- 队列也是一种特殊的线性表,是限制在表的一端进行插入和在另一端进行删除的线性表。
- 表中允许插入的一端称为队尾(rear),允许删除的一端称为队头(front)。
- 当表中没有元素时称为空队列。
- 队列的插入运算称为进队列或入队列,队列的删除运算称为退队列或出队列。
- 入队列的顺序是e1、e2、e3、e4、e5,出队列的顺序为e1、e2、e3、e4、e5,所以队列又称为先进先出线性表(First In First Out),简称FIFO表。其特点是先进先出或者后进后出。
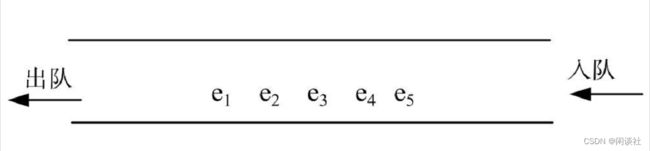
1.顺序—循环队列
顺序存储的队称为顺序队,要分配一块连续的存储空间来存放队列中的元素,并且由于队列的队头和队尾都是活动的,因此有队头、队尾两个指针。这里约定,队头指针指向实际队头元素所在的位置的前一位置,队尾指针指向实际队尾元素所在的位置。
由于顺序队列是静态分配存储,队列的操作是一个动态过程:
- 入队操作是在队尾rear加1的位置插入一个元素,rear移到空间的最后一个位置时队满;
- 出队操作是在队头删除一个元素,不需要移动元素,修改队列头指针front加1。但这种方法存在假溢出的情况。
队列假溢出的情况,是由于在出队删除元素时为了避免移动元素,只是修改了队头指针,这就会造成随着入队、出队的进行,队列整体向后移动,出现了下图所示的情况:队尾指针已经移到最后,再有元素入队就会出现溢出,而事实上,此时队中并未真的“满员”,这种现象为“假溢出”。
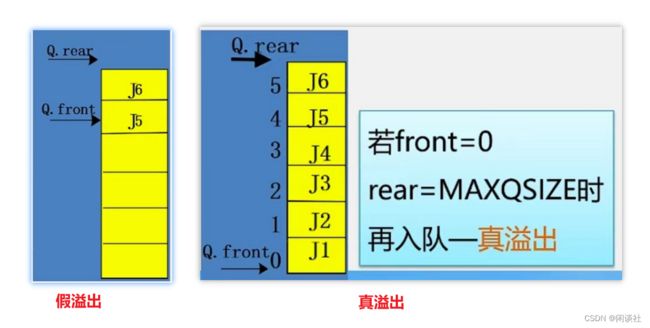
解决假溢出的方法之一是将队列的数据区头尾衔接,且头尾指针关系不变,称为循环队列
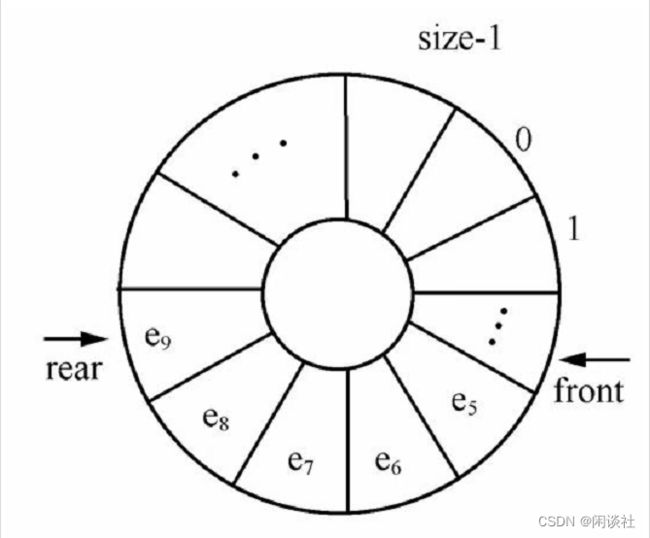
因为是头尾相接的循环结构,入队时的队尾指针加1操作修改为:
rear=(rear+1)% size; (size为顺序队列空间的大小);
出队时的队头指针加1操作修改为:front=(front+1)% size。
这样,当达到size时候,又重新回到0。
队空:front=rear;
队满:如果入队比出队快时,队满条件也是front=rear。因此需要换一种处理方式。
- 1,存储队中元素个数num,当num=0,为空;当num=size,队满
- 2,少用一个元素空间,即当队尾+1时等于队头,视为队满。判定条件:(rear+1)%size=front
下面用第二种判断
typedef int DataType;
class SeqQueue {
private:
DataType* data;
int front;
int rear;
int size;
public:
SeqQueue(int QueueSize = 100) { //构造一个空队列,默认空间大小100
data = new DataType[QueueSize];
front = 0;
rear = 0;
size = QueueSize;
}
~SeqQueue() {
delete[] data;
}
int Empty_Queue(); //判断队列是否为空
int En_Queue(DataType e); //入队将元素e插入队尾
int De_Queue(DataType& e); //出队从队头删除一个元素到e中返回
int Front_Queue(DataType& e); //取队头元素,从队头取出一个元素到e中返回
void Print();
};
int SeqQueue::Empty_Queue() {
return (front == rear);
}
int SeqQueue::En_Queue(DataType e){
if ((rear+1)%size !=front) {
rear = (rear + 1) % size;
data[rear] = e;
return 1;
}
else
{
return 0;
}
}
int SeqQueue::De_Queue(DataType& e) {
if (rear != front) {
front = (front + 1) % size;//因为队列的fron指向头元素的前一位置
e = data[front];
return 1;
}
else
return 0;
}
int SeqQueue::Front_Queue(DataType& e) {
if (rear != front) {
e = data[(front + 1) % size];
return 1;
}
else
return 0;
}
void SeqQueue::Print() {
int i;
i = rear;
while (i != front) {
cout << data[i] << " ";
--i;
}
cout << endl;
}
int main()
{
SeqQueue S;
S.En_Queue(1);
S.En_Queue(2);
S.En_Queue(3);
S.En_Queue(4);
S.Print();
DataType e;
S.De_Queue(e);
S.Print();
cout << e << endl;
system("pause");
return 0;
}
2.链队列
用一个线性链来表示队列,一般用单链表。
头指针和尾指针分别指向链队列的队头和队尾元素,具有头结点。
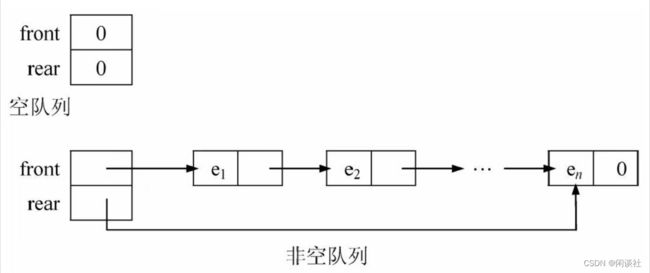
typedef int DataType;
class QueueNode {
public:
DataType data;
QueueNode* next;
};
class LinkNode {
private:
QueueNode* front;;
QueueNode* rear;
public:
LinkNode() {
QueueNode* s = new QueueNode;
s->next = NULL;
front = rear = s;
}
~LinkNode() {
QueueNode* p, * q;
p = front;
while (p) {
q = p;
p = p->next;
delete q;
}
}
int Empty_Queue(); //判断队列是否为空
int En_Queue(DataType e); //将元素e插入队尾
int De_Queue(DataType& e); //从队头删除一个元素到e中返回
int Front_Queue(DataType& e); //从队头取出一个元素到e中返回
void Print();
};
int LinkNode::Empty_Queue() {
return (front ==rear);
}
int LinkNode::En_Queue(DataType e) {
QueueNode* p = new QueueNode;
if (p) {
p->data = e;
p->next = NULL;
rear->next = p;
rear = p;
return 1;
}
else {
return 0;
}
}
int LinkNode::De_Queue(DataType& e) {
QueueNode* p;
if (!Empty_Queue()) {
p = front->next;
e = p->data;
front->next = p->next;
if (p->next==NULL) { //如果删除的是最后一个结点,需要单独处理,令rear=front。否则rear指针会随着p一起被删除
rear = front;
}
delete p;
return 1;
}
else
return 0;
}
int LinkNode::Front_Queue(DataType& e) {
QueueNode* p;
if (!Empty_Queue()) {
p = front->next;
e = p->data;
return 1;
}
else
return 0;
}
void LinkNode::Print() {
QueueNode* p = front->next;
while (p != NULL) {
cout << p->data<<" ";
p = p->next;
}
cout << endl;
}
int main()
{
LinkNode L;
L.En_Queue(1);
L.En_Queue(2);
L.En_Queue(3);
L.Print();
DataType e;
L.Front_Queue(e);
cout << e << endl;
system("pause");
return 0;
}
四、串
constexpr int strLength(char c[]) {
//求串长
int i = 0;
while (c[i] != '\0') {
++i;
}
return i;
}
int StrConcatl(char *c1, char *c2,char *c) {
//链接串c1,c2,组成c
int i = 0, j, len1, len2;
len1 = strLength(c1);
len2 = strLength(c2);
j = 0;
while (c1[j] != '\0') {
c[i] = c1[j];
++i;
++j;
}
j = 0;
while (c2[j] != '\0') {
c[i] = c2[j];
++i;
++j;
}
return 1;
}
int StrSub(char* t, char* s, int i, int len) {
//用t接收串s中从第i个字符开始的长度为len的子串
int slen;
slen = strLength(s);
if (1 < 1 || i > slen || len<0 || len>slen - i + 1) {
cout << "参数不对" << endl;
return 0;
}
int j;
for (j = 0; j <= len; ++j) {
t[j] = s[i + j - 1];
}
t[j] = '\0';
return 1;
}
int StrComp(char* s1, char* s2) {
int i = 0;
while (s1[i] == s2[i] && s1[i] != '\0')
++i;
return (s1[i] == s2[i]);
}
int main()
{
char s1[] = "abcdef";
char s2[] = "english";
char s3[]= "abcdef";
char s[20];
StrConcatl(s1, s2, s);
cout << s << endl;
char t[5];
StrSub(t, s1, 1, 3);
cout << t << endl;
cout << StrComp(s1, s3) << endl;
system("pause");
return 0;
}