C/C++数据结构
1.数据结构与算法概述
1.1数据结构定义
把现实中大量而复杂的问题,以特定的数据类型(个体)和特定的存储结构(个体之间的关系)保存到主存储器(内存)中,以及在此基础之上为实现某个功能(比如查找某个元素,删除某个元素,对所有元素进行排序)而执行的相应操作,这个相应的操作也叫做算法。
数据结构 = 个体 + 个体之间的关系
算法 = 对存储数据的操作
程序 = 数据的存储 + 数据的操作 + 可以被计算机执行的语言
1.2算法概念
算法(algorithm)是指在解决问题时,按照某种机械的步骤一定可以得到问题的结果(有的问题有解,有的没有)的处理过程。算法就是解决这个问题的方法和步骤的描述。
1.2.1衡量算法的标准
1.时间复杂度:大概程序要执行的次数,而非执行的时间
2.空间复杂度:算法执行过程中大概所占用的最大内存
3.难易程度:算法的难易程度
4.健壮性:算法在遇到错误或崩溃时的容错性
1.3数据的存储结构
1.3.1逻辑结构
所谓逻辑结构就是数据与数据之间的关联关系,准确的说是数据元素之间的关联关系。
注:所有的数据都是由数据元素构成,数据元素是数据的基本构成单位。而数据元素由多个数据项构成。
逻辑结构有四种基本类型:集合结构、线性结构、树状结构和网络结构。也可以统一的分为线性结构和非线性结构。
四种基本类型:
(1)集合结构 : 集合结构中的元素关系,除了同属于一个集合这个关系以外,再无其他关系。
(2)线性结构:线性结构中,元素间的关系就是一对一,顾名思义,一条线性的结构。
(3)树形结构:树形结构中,元素间的关系就是一对多,一颗大叔,伸展出的枝叶,也是类金字塔形。
(4)图形结构:图形结构中,元素间的关系就是多对多,举例:一个人可以通过6个人间接认识到世界上的每一个人。类蛛网形。
统一划分:
线性结构:数组、链表 注:栈和队列是特殊的线性结构
非线性结构:树、图
1.3.2物理结构
数据的物理结构就是数据存储在磁盘中的方式。官方语言为:数据结构在计算机中的表示(又称映像)称为数据的物理结构,或称存储结构。它所研究的是数据结构在计算机中的实现方法,包括数据结构中元素的表示及元素间关系的表示。
物理结构一般有四种:顺序存储,链式存储,散列,索引
参考自https://blog.csdn.net/qq_39385118/article/details/80835048
1.4数据结构的重要性
数据结构是编程中的核心
2.数据结构分类:
2.1线性结构(把所有的结点用一根直线穿起来)
2.1.1连续存储 [数组]
数组中元素类型相同,大小相等
优点:
存取速度快效率高
缺点:
需要占用大块连续且连续的内存
在分配内存前必须指定数组的长度
插入和删除元素效率很低
数组的常用操作(C++)
#include 2.1.2离散存储 [链表]
特点:
1)n个结点离散分配
2)彼此通过指针相连
3)每个结点只有一个前驱结点,每个结点只有一个后续结点
4)首结点没有前驱结点,尾结点没有后续结点
优点:
空间没有限制,插入和删除元素速度快
缺点:
存取的速度慢
常用术语:
首结点:第一个有效结点
尾结点:最后一个有效结点
头结点:首结点之前的结点,数据类型与首结点相同。注:头结点不存放有效数据,目的是为了方面对链表的操作
头指针:指向头结点的指针变量(存放头结点的地址)
尾指针 :指向尾结点的指针变量(存放尾结点的地址)
确定链表需要的参数
头指针
链表的分类
单链表
双链表:每个结点有两个指针域
循环链表:能通过任何一个结点找到其他所有的结点
非循环链表
链表常用算法(C++):
#include
{
p = p->pNext;
i++;
}
if (pos - 1 < i || p == NULL)
return false;
PNODE pNew = (PNODE)malloc(sizeof(NODE));//创建新的结点
if (pNew == NULL)
{
cout << "内存分配失败,程序终止!";
exit(-1);
}
pNew->data = value; //对新的结点赋值
PNODE q = p->pNext; //定义临时结点q等于插入位置结点
p->pNext = pNew; //插入位置前的结点指向下一个结点(即插入位置结点)等于新的结点
pNew->pNext = q; //新结点的下一个结点等于插入位置结点(插入后即为插入位置的下一个结点)
}
//删除操作
bool delete_list(PNODE pHead, int pos, int* value)
{
int i = 0;
PNODE p = pHead;
while (p->pNext != NULL && pos-1 > i) //当所要删除的结点不为空时,定义pos-1
{
p = p->pNext;
i++;
}
if (pos-1 < i || p->pNext == NULL)
return false;
PNODE q = p->pNext;
*value = q->data;
p->pNext = q->pNext;
free (q);
q = NULL;
}
算法:
狭义的算法与数据的存储方式密切相关
广义的算法与数据的存储方式无关
泛型:
利用某种技术达到的效果:不同的存储方式,执行的操作是一样的
2.2线性结构的常见应用之一-----栈
定义:一种可以实现“先进后出”的存储结构,只能在栈顶出入,由栈顶指向栈底(从栈顶开始访问)。
分类:
1)静态栈(连续)
类似于数组的结构关系
2)动态栈(不连续)
即链式栈
栈常用算法(C++):
#include 栈的应用:
1)函数的嵌套调用(利用了栈的压栈和出栈)
2)中断
3)表达式求值
4)内存分配
5)缓存处理
6)迷宫
2.3线性结构的常见应用之二-----队列
定义:一种可以实现“先进先出 出”的存储结构,队首出队尾入,由队首指向队尾(从队首开始访问)。
分类:
1)静态队列(用数组实现)
静态队列必须是循环队列
循环队列相关问题:
-
静态队列为什么必须是循环队列?
因为静态队列是基于数组实现的,如果不用循环队列,会导致删除的元素所使用的空间无法继续使用,造成空间的浪费。
-
循环队列需要几个参数来确定?
需要两个参数确定:front表示队头;rear表示队尾
-
循环队列各个参数的含义?
注意:上面两个参数在下面不同的场合有不同的含义
1)队列初始时
front与rear的值都是零
2)队列非空时
front代表队列的第一个元素
rear代表队列最后一个有效元素的下一个元素(不存放有效值)
3)队列为空时
front等于rear,但其值不一定为零
-
循环队列入队伪算法?
第一步:将入队的值存入rear所表示的位置
第二步:更新rear的值:rear = (rear+1)%队列长度
-
循环队列出队伪算法?
直接更新front的值:front = (front+1)%队列长度。
-
如何判断循环队列是否为空?
如果front与rear的值相等,则队列为空。
-
如何判断循环队列是否已满?
两种方式:
1)增加一个标志参数
用参数记录当前有效元素的个数
2)少用一个元素位置(n个位置只用n-1个)
if((r+1)%队列长度==f)
队列已满
else
队列未满
2)链式队列(用链表实现)
循环队列的常用算法(C++):
#include 队列的应用:
所有与时间有关的操作都与队列有关(顺序操作)
3.递归概述
定义:一个函数直接或间接的调用本身
关于函数的调用:
1、当一个函数运行期间调用另一个函数时,在运行被调用函数之前,系统需要完成三件事:
1)将所有的实际参数,返回该函数的地址等信息传递给被调用的函数保存
2)为被调用函数的局部变量(包括形参)分配存储空间
3)将控制转移到被调用函数的入口
2、从被调用函数返回到主调函数之前,系统需要完成的三件事:
1)保存被调用函数的返回结果
2)释放被调用函数所占用的存储空间
3)根据被调用函数之前所保存的主函数地址将控制转移到主调函数
3、当有多个函数相互调用时,按照“后调用的函数先返回先释放空间”的原则,上述函数之间的信息 传递和控制转移必须借助“栈”来实现,系统将整个程序运行时所需要的数据空间安排在一个栈中, 每当调用一个函数时,就在栈顶分配一个存储区域,进行压栈操作,每当一个函数退出时,从栈顶 释放它的存储空间,进行出栈操作,当前运行的函数永远都在栈顶位置。
递归需要满足的三个条件:
1、递归必须得有一个明确的中止条件
2、递归的函数所处理的数据规模必须在递减
3、问题转化到递归后必须时可解的
循环与递归的比较
循环:
优点:速度快、占用存储空间小
缺点:不易被人理解
递归:
优点:易于理解
缺点:速度慢、占用存储空间大
程序举例:(求和、求阶乘、汉诺塔、斐波拉契数列)
#include 递归的应用
树和图的算法、数学方式(例如:斐波那契数列)
4.非线性结构
4.1树
4.1.1树的定义
树是由n(n≥1)个有限节点组成一个具有层次关系的[集合]。把它叫做“树”是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。
4.1.2树的特点
- 一棵树有且只有一个称为根的结点
- 一棵树有若干个互不相交的子树,这些子树本身也是一棵树
- 一棵树由结点和边组成
- 每个结点只有一个父结点,但可以由多个子结点
- 根节点没有父节点
4.1.3专业术语:
深度:从根节点开始到最底层结点的层数称为深度(根节点是第一层)
叶子结点:没有子节点的结点
非终端结点(非叶子结点)
度:子节点的个数称为度
4.1.4树的分类:
一般树:任意一个结点的子节点个数都不受限制
二叉树:任意一个结点的子结点的个数最多为两个,且子节点的位置不可更改(左右顺序:左子树 右子树是有序的),所以二叉树为有序树
二叉树的分类: 1)一般二叉树
2)满二叉树:在不增加树的层数的前提下,无法再多添加一个结点的二叉树称 为满二叉树
3)完全二叉树:如果只删除了满二叉树最底层最右边的连续若干个结点,这样 形成的二叉树就是完全二叉树(满二叉树是完全二叉树的一个 特例)
森林:n个互不相交的树的集合
4.1.5树的存储
思想:把非线性结构的树转化为线性结构存储
二叉树的存储:
1.连续存储【完全二叉树】
优点:查找某个结点的父节点和子节点速度快
缺点:占用内存空间过大
2.链式存储
一般树的存储:
1.双亲表示法 //易于求父节点
2.孩子表示法 //易于求子结点
3.双亲孩子表示法 //结合上面两个的优点
4.二叉树表示法 //把一个普通树转化为二叉树存储(方法:把任意一个结点的左指针域指向 第一个孩子,右指针域指向它的兄弟) 注:一个普通的树转换成二叉树一 定没有右子树。
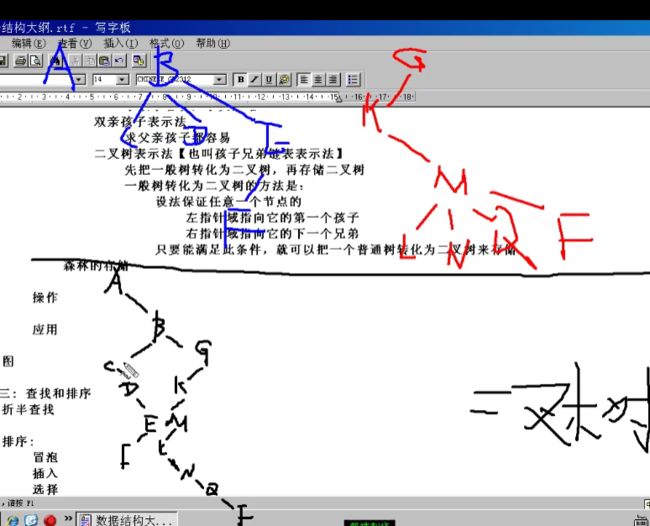
4.1.6森林的存储
同样也是转化为二叉树来存储
方法与普通树转化为二叉树相似,不同的是不同的树之间的关系为兄弟关系,如下图。
4.1.7树的常见操作
1.二叉树的遍历
先序遍历[先访问根节点]:
含义:先访问根节点,再先序遍历左子树,最后先序遍历右子树。
中序遍历[中间访问根节点]:
含义:先中序遍历左子树,再访问根节点,最后中序遍历右子树。
后序遍历[最后访问根节点]:
含义:先后序遍历左子树,再后序遍历右子树,最后访问根节点。
4.1.8已知两种遍历序列求原始二叉树
已知先序和中序或已知中序和后序,可以还原原始二叉树。而已知先序和后序无法确定
1.已知先序和中序求后序遍历序列:
例一:
例二:
2.已知后序和中序求先序遍历序列:
3.二叉树三种遍历的代码实现(C++)
#include 4.1.9树的应用
1.树是数据库中数据组织的一种重要形式
2.操作系统子父进程的关系本身就是一棵树
3.面向对象语言中类的继承关系
4.应用于哈夫曼树
4.2图
6.查找和排序
6.1排序和查找的关系
排序是查找的前提,排序是重点内容。
6.2查找:
6.2.1折半查找
6.3排序:
6.3.1冒泡排序
6.3.2插入排序
6.3.3选择排序
6.3.4快速排序
6.3.5归并排序
pC->pRchild = NULL;
pD->pLchild = NULL;
pD->pRchild = pE;
pE->pLchild = NULL;
pE->pRchild = NULL;
return pA;
}
//先序遍历
void PreTraverseBTree(pBTNODE pT)
{
if (pT != NULL)
{
cout << pT->data << endl;
if (pT->pLchild != NULL)
{
PreTraverseBTree(pT->pLchild);
}
if (pT->pRchild != NULL)
{
PreTraverseBTree(pT->pRchild);
}
}
}
//中序遍历
void InTraverseBTree(pBTNODE pT)
{
if (pT != NULL)
{
if (pT->pLchild != NULL)
{
InTraverseBTree(pT->pLchild);
}
cout << pT->data << endl;
if (pT->pRchild != NULL)
{
InTraverseBTree(pT->pRchild);
}
}
}
//后序遍历
void PosTraverseBTree(pBTNODE pT)
{
if (pT != NULL)
{
if (pT->pLchild != NULL)
{
PosTraverseBTree(pT->pLchild);
}
if (pT->pRchild != NULL)
{
PosTraverseBTree(pT->pRchild);
}
cout << pT->data << endl;
}
}
4.1.9树的应用
1.树是数据库中数据组织的一种重要形式
2.操作系统子父进程的关系本身就是一棵树
3.面向对象语言中类的继承关系
4.应用于哈夫曼树
4.2图
6.查找和排序
6.1排序和查找的关系
排序是查找的前提,排序是重点内容。