《数据结构与算法之二叉搜索树(Java实现)》
说在前头:本人为大二在读学生,书写文章的目的是为了对自己掌握的知识和技术进行一定的记录,同时乐于与大家一起分享,因本人资历尚浅,能力有限,文章难免存在一些错漏之处,还请阅读此文章的大牛们见谅与斧正。若在阅读时有任何的问题,也可通过评论提出,本人将根据自身能力对问题进行一定的解答。
前言
在前面的文章中,我们知道了,有序数组结构在查找某个指定的数据时要比链表结构快,时间复杂度为O(log2N),但插入数据不如链表,复杂度为O(N)。而链表查找数据的时间复杂度为O(N),插入和删除数据时间复杂度为O(1)。
我们可以展开一下思考,有没有那么一种数据结构可以同时满足有序的快查询和链表的快插入?答案是肯定的,这也是本篇文章的重点——二叉树结构。
二叉树结构的概念:一棵树由多个节点组成,其中最上层的节点称为根节点,连接在其下面的的两个节点为其子节点(左节点,右节点),根节点为这两个子节点的父节点。对于没有子节点的节点我们称为叶子节点。
对于二叉树有许多实现方式,本篇文章我们将来探讨二叉搜索树结构,准备好,要发车咯!
01—算法思想
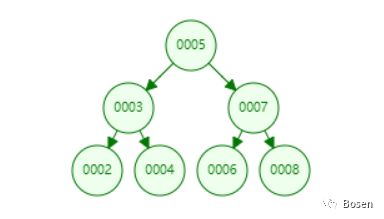
二叉搜索树的特点是,一个节点的左子节点的关键字值小于这个节点,右子节点的关键字值大于或等于这个父节点。(如下图)
在上面的图中,根节点为5,根节点的左右节点分别是3和7,而3的左右节点又为2和4;2,4,6,8都为叶子节点。
通过观察我们不难发现,左子节点总是小于父节点,而右子节点总是大于或等于父节点,这一规则保证了二叉树中数据的有序性。
02—非平衡树
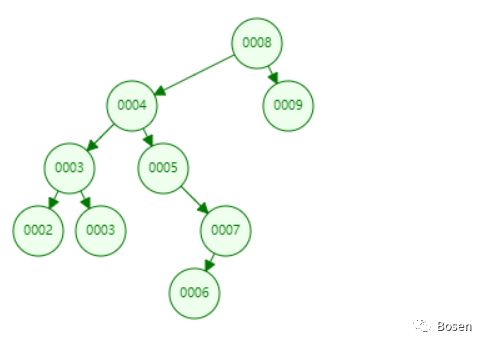
上面展示的二叉树属于一颗理想的二叉搜索树,非常的对称。但在实际的运用中,二叉搜索数并非可以一直保持这种理想的状态(如下图)
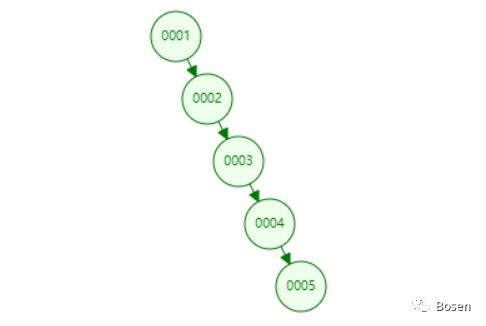
这是由于数据插入时的顺序造成的,当数据较为随机时,结构会更趋于平衡的理想结构,但当数据较为有序时,就会出现上述的情况,最坏的情况可能使树结构退化成链表结构(如下图)
按顺序插入1,2,3,4,5时,这种结构的树从严格意义上已经不能再称得上是树结构了,因为其已经退化成了链表结构,失去了二叉搜索树的优势和特点。介于本文主要介绍二叉搜索树的实现和具体代码实现,对于这种退化情况的处理,我们将会在后面的文章进行详细的讲解,本文不做深入的探讨。
接下来我们将分步使用代码实现二叉搜索树。
03—创建节点类Node
每棵树都由多个节点构成,节点主要用于保存每个数据的值以及数据之间的关系,因此,节点类Node至少需要存在以下三个成员变量:左节点,数据的值,右节点(leftNode,value,rightNode),具体代码参考如下
Node.java
package com.bosen.www;
/**
* 节点类
* @author Bosen 2021/5/31 4:13
*/
public class Node {
public Node leftNode; // 左节点的引用
public int value; // 该节点的数据
public Node rightNode; // 右节点的引用
public Node(Node leftNode, int value, Node rightNode) {
this.leftNode = leftNode;
this.value = value;
this.rightNode = rightNode;
}
}04—构建树的基本骨架
创建一个类BinaryTree,用于表示二叉树,接下来我们需要如何设计这个二叉树?首先我们需要有一个类型为Node的成员变量root表示每棵树的根节点,接下来就是树的基本功能:插入insert,查找find,遍历traverse,删除delete,查找最值findMax,findMin。(下面我们将对每个方法进行分步讲解和实现)
05—查找
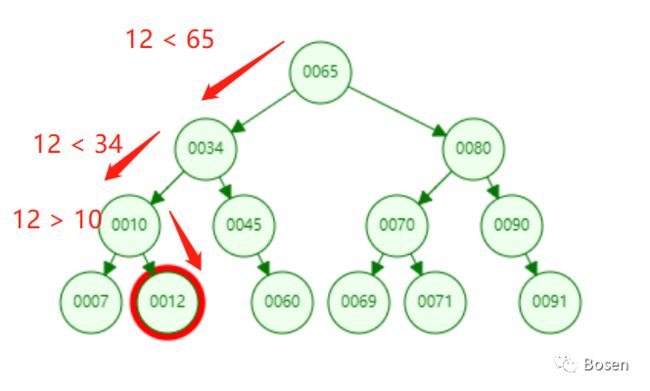
在上面的介绍中,我们得知了二叉搜索树的规则,左子节点小于父节点,父节点小于等于右子节点。所以,当我们需要查找某一个节点时,可以从根节点开始查找,若要查找的数据小于根节点,则下移至其左子节点查找,否则查找其右子节点,直至找到对应的数据位置。下图是数据12的查找过程:
从上面可以看到,我们从根节点65开始遍历比较,因为12小于65,所以需要下移到65的左子节点34进行对比,此时12还是比34小,需要继续对比34的左子节点,来到34的左子节点10,对比发现12比10大,需要下移到10的右子节点比较,这个时候我们成功找到了目标节点12,查找结束。
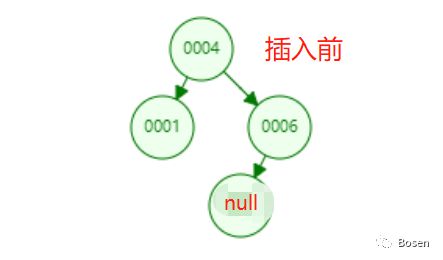
06—插入
对于插入操作,我们需要先从根节点开始遍历查找适合插入的节点,这个过程类似于查找一个不存在的节点。
07—遍历
对于树的遍历有以下三种简单的遍历方法:
-
前序遍历
-
中序遍历
-
后序遍历
其中最常用的是中序遍历,其遍历时保证了数据通过关键字升序访问。我们只需要从根节点开始依次遍历的访问:左节点->本节点->右节点,即可完成中序遍历。下面是中序遍历的具体流程图
08—查找最值
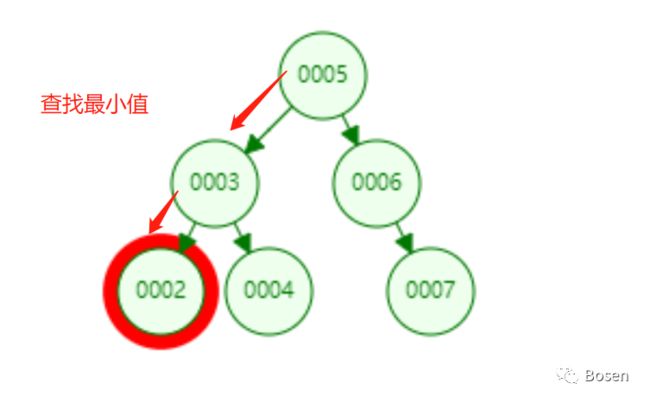
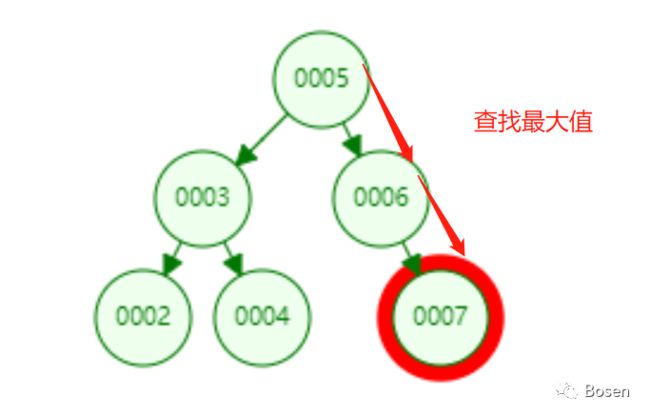
在二叉查找树中,因为其结构的特性,查找最值的实现是十分简单的。查找最小值只需要查找最左节点,最大值查找最右节点即可。
09—删除
删除节点是二叉查找树中最复杂的操作,在删除一个节点前,我们需要考虑三种情况:
-
该节点没有子节点
-
该节点有一个节点
-
该节点有两个节点
第一种情况最简单,对于没有子节点的节点,我们直接删除即可。对于第二种情况只有一个子节点也相对简单,我们需要将原来的节点删除,然后让唯一的子节点顶替原来的节点即可。
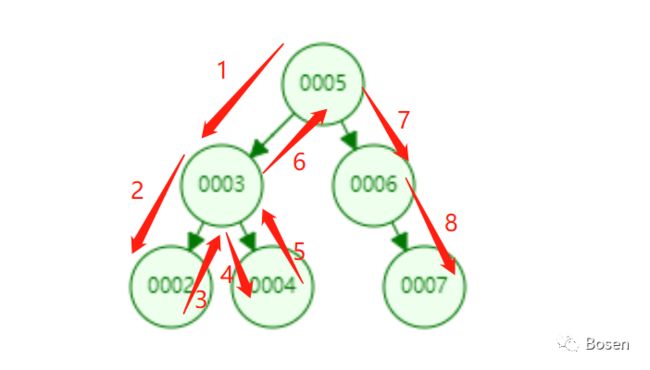
我们重点来谈论第三种情况:要删除的节点有两个子节点。显然我们不能像前两种情况一样直接删除或者简单替换就可以解决的。我们需要对该节点下的子节点进行一定的判断使其能够作为新的父节点。而最适合当这个新的父节点的子节点应该是该节点的中序后继节点(中序后继节点是中序遍历时,关键字比该节点大的节点),删除过程可看下图
10—具体代码
package com.bosen.www;
/**
* 二叉搜索树
* @author Bosen 2021/5/31 4:28
*/
public class BinaryTree {
/*
* 根节点
*/
public Node root;
public BinaryTree(Node root) {
this.root = root;
}
/*
* 插入
*/
public void insert(Node node) {
if (root == null) {
root = node;
return;
}
Node curRoot = root;
while (true) {
if (node.value < curRoot.value) {
if (curRoot.leftNode == null) {
curRoot.leftNode = node;
return;
}
curRoot = curRoot.leftNode;
} else {
if (curRoot.rightNode == null) {
curRoot.rightNode = node;
return;
}
curRoot = curRoot.rightNode;
}
}
}
/*
* 通过关键字查找
*/
public Node find(int key) {
Node curRoot = root;
if (curRoot == null) {
return null;
}
while (curRoot.value != key) {
if (key < curRoot.value) {
curRoot = curRoot.leftNode;// 转向左节点
} else {
curRoot = curRoot.rightNode;// 转向右节点
}
if (curRoot == null) return null;// 未找到结果
}
return curRoot;
}
/*
* 遍历,使用中序遍历
*/
public void traverse(Node curRoot) {
if (curRoot != null) {
traverse(curRoot.leftNode);
System.out.print(curRoot.value+"\t");
traverse(curRoot.rightNode);
}
}
/*
* 通过关键字删除
*/
public void delete(int key) {
if (root == null) {
return;
}
// 找到对应节点
boolean isLeftChild = true; //记录目标节点是否为父节点的左子节点
Node curNode = root; // 需要删除的节点
Node parentNode = null; // 该节点的父节点
while (curNode.value != key) {
parentNode = curNode;
if (key < curNode.value) {
curNode = curNode.leftNode;
} else {
isLeftChild = false;
curNode = curNode.rightNode;
}
if (curNode == null) {
return;// 未找到要删除的节点
}
}
// 要删除的节点没有子节点的情况
if (curNode.leftNode == null && curNode.rightNode == null) {
if (curNode == root) {
root = null;
return;
}
if (isLeftChild) {
parentNode.leftNode = null;// 需要删除的节点在父节点的左节点
} else {
parentNode.rightNode = null;// 需要删除的节点在父节点的右节点
}
return;
}
// 只有一个左节点的情况
if (curNode.leftNode != null && curNode.rightNode == null) {
if (curNode == root) {
root = null;
return;
}
if (isLeftChild) {
parentNode.leftNode = curNode.leftNode;// 使用需要删除节点的左子节点代替
} else {
parentNode.rightNode = curNode.leftNode;// 使用需要删除节点的右子节点代替
}
return;
}
// 只有一个左节点的情况
if (curNode.leftNode == null && curNode.rightNode != null) {
if (curNode == root) {
root = null;
return;
}
if (isLeftChild) {
parentNode.leftNode = curNode.rightNode;// 使用需要删除节点的左子节点代替
} else {
parentNode.rightNode = curNode.rightNode;// 使用需要删除节点的右子节点代替
}
return;
}
// 有两个节点的情况,首先需要找到后继节点
Node successor = curNode.rightNode;
Node successorParent = null;
while (successor.leftNode != null) {
successorParent = successor;
successor = successor.leftNode;
}
// successorParent为空时,表明右子节点为后继节点,直接替换
if (successorParent == null) {
if (curNode == root) {
root = successor;
root.leftNode = curNode.rightNode;
return;
}
if (isLeftChild) {
parentNode.leftNode = successor;
successor.leftNode = curNode.leftNode;
} else {
parentNode.rightNode = successor;
successor.leftNode = curNode.leftNode;
}
}
successorParent.leftNode = successor.rightNode;
successor.rightNode = curNode.rightNode;
if (curNode == root) {
root = successor;
root.leftNode = curNode.leftNode;
return;
}
if (isLeftChild) {
parentNode.leftNode = successor;
successor.leftNode = curNode.leftNode;
} else {
parentNode.rightNode = successor;
successor.leftNode = curNode.leftNode;
}
}
/*
* 查找最大值
*/
public Node findMax() {
Node curRoot = root;
while (curRoot.rightNode != null) {
curRoot = curRoot.rightNode;
}
return curRoot;
}
/*
* 查找最小值
*/
public Node findMin() {
Node curRoot = root;
while (curRoot.leftNode != null) {
curRoot = curRoot.leftNode;
}
return curRoot;
}
}总结
此篇章节我们探讨了二叉搜索树的基本数据结构,并且结合具体代码对二叉树的功能进行实现(前中后序遍历,插入,查找,查找最值,删除)。其中对于二叉搜索树而言,最为复杂的操作是删除操作,需要分开多种情况考虑,也是代码实现的重点。希望阅读完此文章的您,对二叉搜索树能有深刻的理解。
学习资料分享
该资料涵盖Java语法基础、网页编程、数据库、高级框架、spring、springboot、微服务、springcloud(扫描下方二维码关注公众号“Bosen的技术分享栈”,回复“Java”即可领取)
扫描二维码关注
![]()