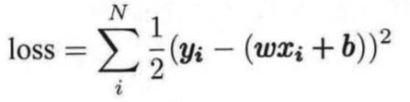深度学习框架PyTorch一书的学习-第三章-Tensor和autograd-1-Tensor

 

参考https://github.com/chenyuntc/pytorch-book/tree/v1.0

希望大家直接到上面的网址去查看代码，下面是本人的笔记

Tensor

Tensor可以是一个数（标量）、一维数组（向量）、二维数组（矩阵）或更高维的数组（高阶数据）

Tensor和numpy的ndarrays类似，不同在于pytorch的tensor支持GPU加速

导包：

from __future__ import print_function
import torch as t

 

判断是否为张量Tensor

a = t.arange(0,6).view(2,3)
a

返回：

tensor([[0, 1, 2],
        [3, 4, 5]])

判断：

t.is_tensor(a) #返回True

 

如果创建的是一个数值

k = 1
t.is_tensor(k)#返回False 

 

1.基础操作

从接口的角度将tensor的操作分为两类：

1）torch.function,如torch.save()等

2）tensor.function,如tensor.view()等

对tensor的大部分操作同时支持这两类接口，如torch.sum(a,b)等价于a.sum(b)

 

从存储角度将tensor的操作分为两类：

1）不会修改自身数据，如new = a.add(b),返回一个新的tensor

2)会修改自身数据，如a.add_(b)，加法结果仍被存储在a中，a的值被修改了

函数名以_结尾的都是inplace方式，即会修改调用者自己数据的函数

 

 

 1）Tensor()

Tensor函数新建tensor是最复杂多变的方式，它既可以接收一个list，并根据list的数据新建tensor；也能够根据指定的形状来新建tensor；还能传入其他的tensor

1》指定形状

#指定tensor的形状
a = t.Tensor(2,3)
a #数值取决于内存空间的状态

返回：

tensor([[1.3733e-14, 6.4069e+02, 4.3066e+21],
        [1.1824e+22, 4.3066e+21, 6.3828e+28]])

 

2》用list数据创建tensor

b = t.tensor([[1,2,3], [4,5,6]])
b

返回：

tensor([[1, 2, 3],
        [4, 5, 6]])

 

1 > 将tensor转换成list——tolist()：

b.tolist()

返回：

[[1, 2, 3], [4, 5, 6]]

 

2> 大小

1.tensor.size()返回torch.Size对象，它是tuple的子类，但其使用方式与tuple略有区别

b_size = b.size()
b_size

返回：

torch.Size([2, 3])

 

2.tensor.shape直接查看tensor的形状

b.shape

返回：

torch.Size([2, 3])

 

3> 元素个数

b.numel() #b中元素总个数，2*3，等价于b.nelement()

都返回6

 

3》创建一个和b形状一样的tensor

c = t.Tensor(b_size)
c

返回：

tensor([[0.0000e+00, 4.6566e-10, 3.8301e+33],
        [3.6902e+19, 2.8026e-45, 0.0000e+00]])

 

4》指定元素创建tensor

d = t.Tensor((2,3))
d

返回：

tensor([2., 3.])

⚠️t.Tensor(*size)创建tensor时，系统不会马上分配空间，只会计算剩余的内存是否足够使用，使用到tensor时才会分配，而其他操作都是在创建完成后马上进行空间分配

 

2.其他操作

 1）ones()

t.ones(2,3)

返回：

tensor([[1., 1., 1.],
        [1., 1., 1.]])

 

2）zeros()

t.zeros(2,3)

返回：

tensor([[0., 0., 0.],
        [0., 0., 0.]])

 

3）arange(s, t, step):得到s到t的值，步长为step,默认为1，前闭后开

t.arange(1,6)

返回：

tensor([1, 2, 3, 4, 5])

 

t.arange(1,6,2)

返回：

tensor([1, 3, 5])

 

也有range():前闭后闭，这个方法已经过时了，建议使用arange()

k = t.range(0,10,2)
k

返回：

tensor([ 0.,  2.,  4.,  6.,  8., 10.])

 

4）linspace(s, e, steps):将s到e均匀分成steps份

t.linspace(1,10,3)

返回：

tensor([ 1.0000,  5.5000, 10.0000])

 

5）randn()标准分布：从标准正态分布(均值为0，方差为 1，即高斯白噪声)中抽取一组随机数

t.randn(2,3)

返回：

tensor([[-0.6179,  0.9102, -0.3926],
        [ 0.8710, -1.5552,  1.3961]])

 

rand()均匀分布：返回一个张量，包含了从区间[0,1)的均匀分布中抽取的一组随机数

t.rand(2,3)

返回：

tensor([[0.3262, 0.9046, 0.6909],
        [0.3090, 0.7856, 0.9516]])

 

6）randperm(m):长度为m，返回一个从0 到m-1 的随机整数排

t.randperm(5)

返回：

tensor([0, 3, 4, 2, 1])

 

7）eye():对角线为1

t.eye(2,3)

返回：

tensor([[1., 0., 0.],
        [0., 1., 0.]])

 

8)等比数列：返回一个1维张量，包含在区间 10^start和 10^end上以对数刻度均匀间隔的steps个点
logspace(start, end, steps, out)

steps:生成的样本数

out(Tensor, optional) : 结果张量

k = t.logspace(-10, 10, 5)
k

返回：

tensor([1.0000e-10, 1.0000e-05, 1.0000e+00, 1.0000e+05, 1.0000e+10])

 

 3.常用Tensor操作

1）tensor.view():用于调整tensor的形状，当然需要保证调整前后元素总数一致

a = t.arange(0,6)
print(a)
a.view(2,3)

返回：

tensor([0, 1, 2, 3, 4, 5])
tensor([[0, 1, 2],
        [3, 4, 5]])

 

view不会修改自身的数据，返回的新tensor与源tensor共享内存，这样只要更改其中一个，另一个也会跟着改变

所以这时候再打印a可见返回仍是之前的样子，没有被改变：

print(a)

返回：

tensor([0, 1, 2, 3, 4, 5])

 

参数为-1的作用：当某一个维度设置为-1时，计算机会自动根据另一个维度的大小去计算该维度的值

b = a.view(-1, 3)
b

返回：

tensor([[0, 1, 2],
        [3, 4, 5]])

 

这时候改变a可以发现b也跟着改变，因为共享内存：

a[1] = 100
b

返回：

tensor([[  0, 100,   2],
        [  3,   4,   5]])

 

2）squeeze/unsqueeze:需要添加或减少某一维度,不会更改原来的数据，而是生成新的tensor

1》unsqueeze(i):在i位置添加维度1

b.unsqueeze(1)

返回：

tensor([[[0, 1, 2]],

        [[3, 4, 5]]])

即b从2*3变成了2*1*3

等价于：

b.unsqueeze(-2) #表示倒数第二个维度

 

2》squeeze(i):删除i位置的维度1

c = b.view(1,1,1,2,3)
c

返回：

tensor([[[[[0, 1, 2],
           [3, 4, 5]]]]])

 

c.squeeze(0) #删除第0维的1

返回：

tensor([[[[0, 1, 2],
          [3, 4, 5]]]])

可见从1*1*1*2*3变成了1*1*2*3

 

可以不指定位置，默认是删除所有的1维度：

c.squeeze()

返回：

tensor([[0, 1, 2],
        [3, 4, 5]])

可见从1*1*2*3变为了2*3

 

3）resize:用来调整size，与view的区别在于它可以修改原来tensor的尺寸

1》如果小于，则之前的数据依然会被保存

b.resize_(1,3)

返回，这里因为上面修改过：

tensor([[  0, 100,   2]])

 

2》如果新尺寸超过了原尺寸，就会自动分配新的内存空间；

b.resize_(3,3)

返回：

tensor([[  0, 100,   2],
        [  3,   4,   5],
        [  0,   0,   0]])

可见上面小于的操作并没有丢失超出的数据

 

4）索引操作

索引出来的结果与原tensor共享内存，即修改一个，另一个也会跟着修改

a[0] #第0行

返回：

tensor([ 1.7488, -0.5191, -0.4163,  0.3690])

 

a[:,0] #第0列

返回：

tensor([ 1.7488, -1.9458,  1.1511])

 

a[0][2]#第0行第2个元素

返回：

tensor(-0.4163)

 

a[0,-1] #第0行最后一个元素

返回：

tensor(0.3690)

 

a[:2] #前两行，省略列则默认所有列

返回：

tensor([[ 1.7488, -0.5191, -0.4163,  0.3690],
        [-1.9458, -0.1565,  1.4890, -0.0370]])

 

a[:2,0:2] #前两行，第0，1列

返回：

tensor([[ 1.7488, -0.5191],
        [-1.9458, -0.1565]])

 

print(a[0:1, :2]) #两者等价，第0行，前两列
print(a[0, :2])

返回：

tensor([[ 1.7488, -0.5191]])
tensor([ 1.7488, -0.5191])

 

a > 1 #判断a中大于1的值，大于为1，小于为0

返回：

tensor([[1, 0, 0, 0],
        [0, 0, 1, 0],
        [1, 0, 0, 0]], dtype=torch.uint8)

 

a[a>1]#得到大于1的值，等价于a.masked_select(a>1),结果与原tensor不共享内存空间

返回：

tensor([1.7488, 1.4890, 1.1511])

 

a[t.LongTensor([0,1])] #第0，1行

返回：

tensor([[ 1.7488, -0.5191, -0.4163,  0.3690],
        [-1.9458, -0.1565,  1.4890, -0.0370]])

 

5）常用选择函数：

1》gather：是一个比较复杂的操作,并不会更改原数据

dim和index的设置之间的关系是，对于一个二维tensor：

out[i][j] = input[index[i][j]][j] #当dim = 0时
out[i][j] = input[i][index[i][j]] #当dim = 1时

如果是一个三维tensor：

out[i][j][k] = input[index[i][j][k]][j][k] #当dim = 0时
out[i][j][k] = input[i][index[i][j][k]][k] #当dim = 1时
out[i][j][k] = input[i][j][index[i][j][k]] #当dim = 2时

可见dim设置为什么，对应的维度的索引就由index[i][j][k]来替换

 

举个二维的例子：

1.

a = t.Tensor([[1,2],[3,4]])
a

⚠️index的类型必须是LongTensor类型的

#将第0行，第一个元素改成第0个元素
#将第二行元素互换
index = t.LongTensor([[0,0],[1,0]])
a.gather(1, index)

返回：

tensor([[1., 1.],
        [4., 3.]])

 

2.

a = t.arange(0,16).view(4,4)
a

 

#选取对角线的元素
index = t.LongTensor([[0,1,2,3]])
index.size()

返回：

torch.Size([1, 4])

a.gather(0,index)

返回：

tensor([[ 0,  5, 10, 15]])

只定义了第一行的index，所以只会得到a[0][0] = a[0][0],a[0][1] = a[1][1],a[0][2] = a[2][2],a[0][3] = a[3][3],其他行因为没有index，所以不会得到值，所以得到了对角线的值，该index更改了a第一个索引的下标

 

index = t.LongTensor([[3,2,1,0]])
index

返回：

tensor([[3, 2, 1, 0]])

使用.t()进行转置，返回4*1

index = t.LongTensor([[3,2,1,0]]).t()
index

返回：

tensor([[3],
        [2],
        [1],
        [0]])

使用转置后的index实现选取对角线的元素

a.gather(1,index)

返回：

tensor([[ 3],
        [ 6],
        [ 9],
        [12]])

即得到a[0][0] = a[0][3],a[1][0] = a[1][2],a[2][0] = a[2][1],a[3][0] = a[3][0]

 

#选取两个对角线的元素
index = t.LongTensor([[0,1,2,3],[3,2,1,0]]).t()
index

返回：

tensor([[0, 3],
        [1, 2],
        [2, 1],
        [3, 0]])

 

b = a.gather(1,index)
b

返回：

tensor([[ 0,  3],
        [ 5,  6],
        [10,  9],
        [15, 12]])

 

gather的逆操作是scatter_:out = scatter_(dim, index, input)

gather把数据从input中按index取出

scatter_把取出的数据再放回去

#把上面得到的两个对角线元素分别放进原来位置
c = t.zeros(4,4)
c.scatter_(1,index,b.float())

返回：

tensor([[ 0.,  0.,  0.,  3.],
        [ 0.,  5.,  6.,  0.],
        [ 0.,  9., 10.,  0.],
        [12.,  0.,  0., 15.]])

⚠️如果上面不写成b.float()会报错：

RuntimeError: Expected object of scalar type Float but got scalar type Long for argument #4 'src'

 

2》index_select(input, dim, index, out=None):->Tensor

沿着指定维度对输入进行切片，取index中指定的相应项，index是一个LongTensor，然后返回一个新的张量。返回的张量与原始张量在指定轴上有着相同的维度

返回的张量与原始张量不共享内存空间

a = t.rand(2,3)
a

返回：

tensor([[0.1724, 0.9527, 0.1607],
        [0.9276, 0.1666, 0.6390]])

 

a_select = t.index_select(a, 1, t.LongTensor([0,2]))
a_select

返回：

tensor([[0.1724, 0.1607],
        [0.9276, 0.6390]])

 

3》masked_select(input, mask, out=None)

根据传入的ByteTensor类型的mask，来得到1所对应的元素，返回一个一维张量

张量 mask和input张量必须有相同数量的元素数目，但形状或维度不需要相同

返回的张量与原始张量不共享内存空间

a = t.rand(2,3)
a

返回：

tensor([[0.1724, 0.9527, 0.1607],
        [0.9276, 0.1666, 0.6390]])

 

mask = t.ByteTensor([[0, 1, 0], [1, 1, 0]])
a_mask = t.masked_select(a, mask)
a_mask

返回：

tensor([0.9527, 0.9276, 0.1666])

 

4》nonzero(input, out=None)选择非零值

返回一个包含输入input中非零元素索引的张量,输出张量中的每行包含输入中非零元素的索引

a = t.Tensor([[1, 0, 3, 0, 2], [0, 2, 0, 2, 1]])
a

返回：

tensor([[1., 0., 3., 0., 2.],
        [0., 2., 0., 2., 1.]])

 

a_nonzero = t.nonzero(a) #返回的是非零元素的索引
a_nonzero

返回：

tensor([[0, 0],
        [0, 2],
        [0, 4],
        [1, 1],
        [1, 3],
        [1, 4]])

 

6）高级索引——一般不与原始的Tensor共享内存

x = t.arange(0,27).view(3,3,3)
x

返回：

tensor([[[ 0,  1,  2],
         [ 3,  4,  5],
         [ 6,  7,  8]],

        [[ 9, 10, 11],
         [12, 13, 14],
         [15, 16, 17]],

        [[18, 19, 20],
         [21, 22, 23],
         [24, 25, 26]]])

 

同时访问两个值：

x[[1,2], [1,2], [2,0]] #访问的是x[1,1,2]和x[2,2,0]

返回：

tensor([14, 24])

 

同时访问三个值：

x[[2,1,0], [0], [1]] #访问的是x[2, 0, 1],x[1, 0, 1],x[0, 0, 1]

返回：

tensor([19, 10,  1])

 

...代表剩下的都取：

x[[0, 2], ...] #取x[0],x[2]

返回：

tensor([[[ 0,  1,  2],
         [ 3,  4,  5],
         [ 6,  7,  8]],

        [[18, 19, 20],
         [21, 22, 23],
         [24, 25, 26]]])

 

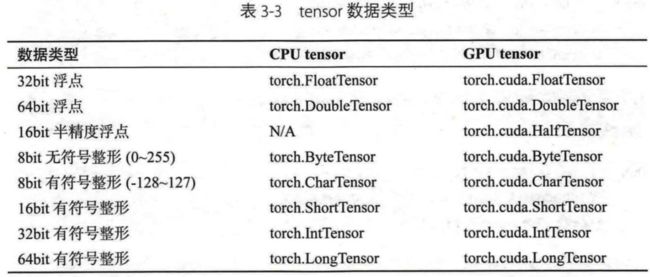
4.Tensor类型

 Tensor有不同的数据类型，每种类型分别对应有CPU和GPU版本（HalfTensor除外）

默认的tensor类型是FloatTensor，可通过t.set_default_tensor_type()修改默认的tensor类型（如果默认类型为GPU tensor，则所有操作都将在GPU上进行）

tensor的类型对分析内存占用很有帮助

比如一个size为(1000, 1000, 1000)的FloatTensor，它有1000*1000*1000 = 10^9个元素，每个元素占32bit/8 = 4 Byte字节内存，所以这整个tensor占4GB内存/显存

HalfTensor是专门为GPU版本设计的，同样的元素个数，显存占用只有FloatTensor的一半，所以可以极大地缓解GPU显存不足的问题，但由于HalfTensor所能表示的数值大小和精度有限，所以可能出现溢出等问题

各数据类型之间可以相互转换，type(new_type)是通用的做法，当然，你也可以使用.float(),.long(),.half()等快捷方法

CPU和GPU tensor之间的互相转换通过tensor.cuda和tensor.cpu的方法实现

Tensor还有一个new方法，用法和t.Tensor一样，会调用该tensor对应类型的构造函数，生成与当前tensor类型一致的tensor

 

首先查看一下默认的tensor类型：

t.get_default_dtype()

返回：

torch.float32

 

想将默认类型设置为IntTensor类型，但是出错：

#设置默认tensor，注意参数是字符串
t.set_default_tensor_type('torch.IntTensor')

报错：

TypeError: only floating-point types are supported as the default type

意思是说只能设置float类型的值为默认类型,所以设置为torch.CharTensor也会报错，只能设置为float，double和half

如果设置为：

#设置默认tensor，注意参数是字符串
t.set_default_tensor_type('torch.DoubleTensor')

就成功：

t.get_default_dtype()

返回：

torch.float64

 

然后生成一个值

a = t.Tensor(2, 3)
a

返回：

tensor([[-1.2882e-231,   1.7306e-77,   6.2817e+98],
        [ 7.7417e-315, -1.2882e-231,  4.2154e-309]])

查看该值的类型：

a.dtype #返回a的类型

果然是float64的类型：

torch.float64

 

把a转成FloatTensor类型，等价于b = a.type(t.FloatTensor)

b = a.float()
b

返回：

tensor([[-0., 0., inf],
        [0., -0., 0.]], dtype=torch.float32)

对于32bit的float来说，上面生成的double值都过大或过小，超过其能承受范围了

 

type_as(tensor): 等价于self.type(tensor.type())，将tensor投射为参数给定tensor类型并返回。 如果tensor已经是正确的类型则不会执行操作

c = a.type_as(b)
c

返回：

tensor([[-0., 0., inf],
        [0., -0., 0.]], dtype=torch.float32)

即将a投射为b的类型，然后将值返回到c中，因为溢出，所以c的值和b相同

两者不共享内存空间

c[0] = 1.0
c

返回：

tensor([[1., 1., 1.],
        [0., -0., 0.]], dtype=torch.float32)

a不变

 

new(): 构建一个有相同数据类型的tensor

此时a为：

tensor([[0., 0., 0.],
        [0., 0., 0.]])

生成b：

d = a.new(2,3)
d

返回：

tensor([[0., 0., 0.],
        [0., 0., 0.]])

恢复之前的设置：

t.set_default_tensor_type('torch.FloatTensor')

 

5.逐元素操作

对tensor的每一个元素（point-wise,又名element-wise）进行操作，此操作的输入与输出形状一致

当然，上面的一些操作如div,mul,pow,fmod等都实现了运算符重载，可以直接使用运算符

如a**2等价于torch.pow(a, 2), a*2等价于torch.mul(a, 2)，a%2等价于torch.fmod(a,2)

 

1)clamp: 常用在某些需要比较大小的地方，如取一个tensor的每个元素与另一个数的较大值

a = t.arange(0, 6).view(2,3)
a

返回：

tensor([[0, 1, 2],
        [3, 4, 5]])

比较大小：

t.clamp(a, min=3) #取a中元素与3相比其中最大的值

返回：

tensor([[3, 3, 3],
        [3, 4, 5]])

 

6.归并操作

此操作会使输出形状小于输入形状，并可以沿着某一维度进行指定操作

比如操作.sum()，既可以计算整个tensor的和，也可以计算tensor中每一行或每一列的和

上面的操作都有一个参数dim，用来指定这些操作是在哪个维度上执行的

如输入的形状是(m, n, k)

• 如果指定dim = 0,输出的形状就是(1,n,k)或(n,k),即对行进行操作
• 如果指定dim = 1,输出的形状就是(m,1,k)或(m,k),即对列进行操作
• 如果指定dim = 2,输出的形状就是(m,n,1)或(m,n),即对第三维进行操作

输出size中是否有1将取决于参数keepdim,如果keepdim = True则会保留维度1，这里keepdim默认为False

但并不是所有的函数都符合这种形状变化方式，如cumsum

 

b = t.ones(2,3)
#进行求和操作
b.sum(dim = 0, keepdim = True)

返回：

tensor([[2., 2., 2.]])

查看此时的size：

b.sum(dim = 0, keepdim = True).size()

返回：

torch.Size([1, 3])

如果这里不设keepdim = True，效果为：

b.sum(dim = 0)

返回：

tensor([2., 2., 2.])

大小为：

torch.Size([3])

 

如果将dim设置为1

b.sum(dim=1)

返回：

tensor([3., 3.])

 

cunsum有自己的计算方式,是每行逐层进行累加：

a = t.arange(0,6).view(2,3)
print(a)
a.cumsum(dim=1)#沿着行累加

返回：

tensor([[0, 1, 2],
        [3, 4, 5]])
tensor([[ 0,  1,  3],
        [ 3,  7, 12]])

 

7.比较函数

这些函数有逐元素的，也有类似归并操作的

其中第一行的比较操作实现了运算符重载，等价于a>=b,a>b,a!=b和a==b,其返回结果是一个ByteTensor,可用来选取元素

max/min这两个操作比较特殊，以max为例：

• t.max(tensor) : 返回tensor中最大的一个数
• t.max(tensor, dim) : 指定维上最大的数，返回tensor和下标
• t.max(tensor1, tensor2) : 比较两个tensor，得到对应位置比较大的元素

 

1）比较函数

a = t.linspace(0,15,6).view(2,3)
a

返回：

tensor([[ 0.,  3.,  6.],
        [ 9., 12., 15.]])

 

b = t.linspace(15, 0, 6).view(2,3)
b

返回：

tensor([[15., 12.,  9.],
        [ 6.,  3.,  0.]])

比较：

a>b

返回：

tensor([[0, 0, 0],
        [1, 1, 1]], dtype=torch.uint8)

uint8就是ByteTensor类型

然后我们就能够使用上面得到饿结果去获取a>b的值：

a[a>b]

返回：

tensor([ 9., 12., 15.])

大小为：

torch.Size([3])

 

2）最值函数

#既max(tensor):得到tensor中最大的值
t.max(a)

返回：

tensor(15.)

 

t.max(b, dim=0)#得到的是列中最大的值
#第一个返回值是最大的值
#第二个返回值是这些值是该列的第几个元素

返回：

(tensor([15., 12.,  9.]), tensor([0, 0, 0]))

 

t.max(b, dim=1)#得到的是行中最大的值
#第一个返回值是最大的值
#第二个返回值是这些值是该行的第几个元素

返回：

(tensor([15.,  6.]), tensor([0, 0]))

 

比较两个tensor：

t.max(a, b)

返回：

tensor([[15., 12.,  9.],
        [ 9., 12., 15.]])

 

3）比较一个tensor和一个数，可以使用clamp函数

#将a中各个位置的值和10比较，得到其中更大的值
t.clamp(a, min=10)

返回：

tensor([[10., 10., 10.],
        [10., 12., 15.]])

 

8.线性代数

 

1）trace() → float

a = t.Tensor([[1, 0, 3], [0, 2, 0], [1, 1, 1]])
a

求对角线元素之和：

k = t.trace(a) #1+2+1
k

返回值的类型是floatTensor：

tensor(4.)

 

2）diag():得到对角线元素

k = t.diag(a)
k

返回：

tensor([1., 2., 1.])

 

3）triu(input, diagonal=0, out=None) → Tensor上三角/tril()下三角

偏移量diagonal默认为0

u = t.triu(a)#上三角
u

返回：

tensor([[1., 0., 3.],
        [0., 2., 0.],
        [0., 0., 1.]])

 

l = t.tril(a) #下三角
l

返回：

tensor([[1., 0., 0.],
        [0., 2., 0.],
        [1., 1., 1.]])

 

偏移量:

• diagonal = 0，保留主对角线与主对角线以上/下的元素；
• diagonal = n，保留主对角线与主对角线向上/下n行的元素；
• diagonal = -n，保留主对角线上/下方h行后的对角线的元素；

l1 = t.tril(a, diagonal=1) #下三角,既除了下三角还多得到斜对角向上多一行的值
l1

返回：

tensor([[1., 0., 0., 0., 0.],
        [0., 2., 0., 0., 0.],
        [1., 1., 1., 2., 0.],
        [1., 3., 4., 5., 2.],
        [3., 2., 1., 1., 2.]])

 

l2 = t.tril(a, diagonal=2) #下三角,既除了下三角还多得到斜对角向上多两行的值
l2

返回：

tensor([[1., 0., 3., 0., 0.],
        [0., 2., 0., 3., 0.],
        [1., 1., 1., 2., 2.],
        [1., 3., 4., 5., 2.],
        [3., 2., 1., 1., 2.]])

 

l3 = t.tril(a, diagonal=-2) #下三角，得到从对角线开始删除两行的值
l3

返回：

tensor([[0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0.],
        [1., 0., 0., 0., 0.],
        [1., 3., 0., 0., 0.],
        [3., 2., 1., 0., 0.]])

 

4)torch.mm(mat1, mat2, out=None) → Tensor矩阵乘法

对矩阵mat1和mat2进行相乘。 如果mat1 是一个n*m张量，mat2 是一个 m*p 张量，将会输出一个 n×p 张量out

z1 = t.Tensor([[1,2,3],[2,3,4]])
z1

返回：

tensor([[1., 2., 3.],
        [2., 3., 4.]])

 

z2 = t.Tensor([[1,2],[3,4],[5,6]])
z2

返回：

tensor([[1., 2.],
        [3., 4.],
        [5., 6.]])

相乘

t.mm(z1, z2)

返回：

tensor([[22., 28.],
        [31., 40.]])

 

5）转置

矩阵的转置会导致存储空间不连续，需要调用其的.contiguous方法将其转为连续

b = a.t()
b.is_contiguous() #查看空间是否连续

返回：

False

但是显示b为：

tensor([[ 0.,  9.],
        [ 3., 12.],
        [ 6., 15.]])

与调用.contiguous方法返回的值是相同的

b.contiguous().is_contiguous() #返回true

 

9.Tensor和Numpy

Numpy和Tensor共享内存

由于Numpy历史悠久，支持丰富的操作，所以当遇见Tensor不支持的操作的时候，可以先将其转成Numpy，处理完后再转回tensor，其转换开销很小

import numpy as np
a = np.ones([2,3], dtype = np.float32)
a

返回：

array([[1., 1., 1.],
       [1., 1., 1.]], dtype=float32)

 

b = t.from_numpy(a)
b

返回：

tensor([[1., 1., 1.],
        [1., 1., 1.]])

查看b类型：

b.dtype

 

#另一种生成b的方法,这种情况下若numpy不是float32则会新建
b = t.Tensor(a)
b

返回相同

 

c = b.numpy()
c

返回：

array([[1., 1., 1.],
       [1., 1., 1.]], dtype=float32)

 

#a,b,c共享内存,一个改变，其他的也跟着改变
a[0,1] = 100
a

返回：

array([[  1., 100.,   1.],
       [  1.,   1.,   1.]], dtype=float32)

查看b,c的值发现也是这个

 

10.自动广播

• pytorch支持自动广播法则 ：快速执行向量化的同时不会占用额外的内存/显存

法则定义：

• 让所有输入数组向其中shape最长的数组看弃，shape不足的数组在前面添加1
• 当输入法则的某个维度的长度为1时，计算时沿此维度复制扩充成一样的形状

a = t.ones(3,2) #二维
b = t.zeros(2,3,1) #三维
a+b

返回：

tensor([[[1., 1.],
         [1., 1.],
         [1., 1.]],

        [[1., 1.],
         [1., 1.],
         [1., 1.]]])

自动广播法则为：

1. 因为a比b少1维，所以在a前面补1,形状变为(1,3,2)。等价于a.unsqueeze(0)

2.a和b的第一和三维形状不一样，进行扩展，将他们的形状都变成(2,3,2)

 

• 也可以通过函数实现手动广播，这样更直观，更不易出错：

unsqueeze或view ： 为数据某一维的形状补1

expand或expand_as :重复数组，该操作不会复制数组，所以不会占用额外空间

⚠️repeat实现与expand相类似的功能，不使用它的原因是repeat会把相同数据复制多份，因此会占用额外的空间

既上面的例子可以写成：

a.unsqueeze(0).expand(2,3,2) + b.expand(2,3,2)

 

11.内部结构

tensor分为头信息区（Tensor）和存储区（Storage）

信息区主要保存着tensor的形状（size）、步长（stride）、数据类型（type）等信息，而真正的数据则保存成连续数组，存储在存储区

因为数据动辄成千上万，因此信息区元素占用内存较少，主要内存占用取决于tensor中元素的数目，即存储区的大小

 

一般来说，一个tensor有着与之相对应的storage，storage是在data之上封装的接口，便于使用

不同的tensor的头信息一般不同，但是可能使用相同的storage

生成a:

a = t.arange(0,6)
a.storage()

⚠️将这里改成a = t.arange(0,6).float()，用来保证得到的值的类型为FloatTensor

这跟下面遇见的一个问题相关，可以看到下面了解一下，然后再跟着操作

所以你的下面内容的值的类型应该为FloatTensor类型，我的仍是LongTensor，因为我没有改过来

返回：

0
 1
 2
 3
 4
 5
[torch.LongStorage of size 6]

生成b:

b = a.view(2,3)
b.storage()

返回：

 0
 1
 2
 3
 4
 5
[torch.LongStorage of size 6]

对比两者内存地址：

#一个对象的id值可以看作她的内存空间
#a,b storage的内存地址一样，即是同一个storage
id(a.storage()) == id(b.storage())

返回：

True

改变某个值查看是否共享内存：

#a改变，b也随之改变，因为他们共享storage，即内存
a[1] = 100
b

返回：

tensor([[  0, 100,   2],
        [  3,   4,   5]])

生成c:

#c从a的后两个元素取起
c = a[2:]
c.storage()#指向相同

返回：

 0
 100
 2
 3
 4
 5
[torch.LongStorage of size 6]

查看其首元素内存地址：

c.data_ptr(), a.data_ptr() #data_ptr返回tensor首元素的内存地址
#从结果可以看出两者的地址相差16
#因为c是从a第二个元素选起的，每个元素占8个字节，因为a的值的类型是int64

返回：

(140707162378192, 140707162378176)

因为查看后a的类型为int64:

a.dtype

返回：

torch.int64

更改c:

c[0] = -100 #a,c也共享内存空间，c[0]的内存地址对应的是a[2]的内存地址
a

返回：

tensor([   0,  100, -100,    3,    4,    5])

 

使用storage来生成新tensor：

d = t.Tensor(c.storage())#这样a,b,c,d共享同样的内存空间
d[0] = 6666
b

⚠️报错：

RuntimeError: Expected object of data type 6 but got data type 4 for argument #2 'source'

这是因为Tensor期待得到的值的类型是FloatTensor（类型6），而不是其他类型LongTensor(data type 4)

因为如果生成：

dtypea = t.FloatTensor([[1, 2, 3], [4, 5, 6]])
dtypea.storage()

返回：

 1.0
 2.0
 3.0
 4.0
 5.0
 6.0
[torch.FloatStorage of size 6]

再运行就成功了：

d = t.Tensor(dtypea.storage())#这样a,b,c,d共享同样的内存空间
d[0] = 6666
dtypea

返回：

tensor([[6.6660e+03, 2.0000e+00, 3.0000e+00],
        [4.0000e+00, 5.0000e+00, 6.0000e+00]])

如果使用的是IntTensor（data type 3）,也会报错：

RuntimeError: Expected object of data type 6 but got data type 3 for argument #2 'source'

ShortTensor(data type 2),CharTensor(data type 1),ByteTensor(data type 0),DoubleTensor(data type 7)

 

下面的操作会在将上面的值改成FloatTensor的基础上进行，即在a = t.arange(0,6)后面添加.float()，然后从头执行了一遍

d = t.Tensor(c.storage())#这样a,b,c,d共享同样的内存空间
d[0] = 6666
b

返回：

tensor([[ 6.6660e+03,  1.0000e+02, -1.0000e+02],
        [ 3.0000e+00,  4.0000e+00,  5.0000e+00]])

判断是否共享内存：

#因此a,b,c,d这4个tensor共享storage
id(a.storage()) ==id(b.storage()) ==id(c.storage()) ==id(d.storage())#返回True

偏移量：

#获取首元素相对于storage地址的偏移量
a.storage_offset(), c.storage_offset(), d.storage_offset()

返回：

(0, 2, 0)

即使使用索引只获得一部分值，指向仍是storage：

#隔两行/列取元素来生成e
e = b[::2,::2]
print(e)
print(e.storage_offset())
id(e.storage()) ==id(a.storage()) #虽然值不相同，但是得到的storage是相同的

返回：

tensor([[6666., -100.]])
0
Out[44]:
True

步长信息：是有层次结构的步长

#获得步长信息
b.stride(), e.stride()

返回：

((3, 1), (6, 2))

查看空间是否连续：

#查看其值的内存空间是否连续
#因为e只取得了storage中的部分值，因此其是不连续的
b.is_contiguous(), e.is_contiguous()

返回：

(True, False)

从上面的操作中我们可以看出绝大多数的操作并不修改tensor的数据，即存储区的内容，只是修改了头信息区的内容

这种做法更节省内存，同时提升了处理速度

但是我们可以看见e的操作导致其不连续，这时候可以调用tensor.contiguous()方法将他们变成连续的数据。该方法是复制数据到新的内存中，不再与原来的数据共享storage，如：

e.contiguous().is_contiguous() #返回True

生成f:

print(e.data_ptr())
f = e.contiguous()
print(f.data_ptr()) #可见为f新分配了内存空间
print(f)
print(f.storage())#内存空间中只有两个值
print(f.size()) 
print(e.data_ptr()) #e指向的内存没有改变
f.is_contiguous() #这里的f的内存空间是连续的

返回：

140707203003760
140707160267104
tensor([[6666., -100.]])
 6666.0
 -100.0
[torch.FloatStorage of size 2]
torch.Size([1, 2])
140707203003760
Out[56]:
True

是否为连续内存空间有什么影响？
比如当你想要使用.view()转换tensor的形状时，如果该tensor的内存空间不是连续的则会报错：

k = t.arange(0,6).view(2,3).float().t()#进行转置，转置后的k内存是不连续的
k.is_contiguous()
k.view(-1)

报错：

RuntimeError: invalid argument 2: view size is not compatible with input tensor's size and stride (at least one dimension spans across two contiguous subspaces). Call .contiguous() before .view(). at /Users/soumith/mc3build/conda-bld/pytorch_1549593514549/work/aten/src/TH/generic/THTensor.cpp:213

报错的意思也是要求在.view()之前调用.contiguous(),改后为：

k = t.arange(0,6).view(2,3).float().t()#进行转置，转置后的k内存是不连续的
k.is_contiguous()
k.contiguous().view(-1)

成功返回：

tensor([0., 3., 1., 4., 2., 5.])

 

12.其他与tensor相关内容

1）持久化

Tensor的保存和加载十分简单，使用t.save和t.load即可完成相应的功能

在save/load时可指定使用的pickle模块，在load时还可以将CPU tensor映射到CPU或其他GPU上

if t.cuda.is_available():
    a = a.cuda(1) #把a转为GPU1上的tensor
    t.save(a, 'a.pth')
    #加载为b,存储与GPU1上（因为保存时tensor就在GPU1上）
    b = t.load('a.pth')
    #加载为c，存储于CPU
    c = t.load('a.pth', map_location = lambda storage, loc:storage)
    #加载为d,存储于GPU0上
    d = t.load('a.pth', map_location={'cuda:1':'cuda:0'})

 

2)向量化

向量化计算是一种特殊的并行计算方式，一般程序在同一时间只执行一个操作的方法，它可以在同一时间执行多个操作，通常是对不同的数据执行同样的一个或一批指令，或者说把指令应用于一个数组/向量上

向量化可极大程度地提高科学运算的效率，用来替代python中的for循环

举例说明：

def for_loop_add(x,y):
    result = []
    for i,j in zip(x,y):
        result.append(i+j)
    return t.Tensor(result)

生成x,y:

x = t.zeros(100)
y = t.ones(100)

使用for循环：

import time
start = time.time()
for_loop_add(x,y)
end = time.time()
end-start

返回：

0.0022869110107421875

向量化：

import time
start = time.time()
x+y
end = time.time()
end-start

返回：

0.00030493736267089844

可见时间有近十倍的差距

⚠️有几点需要注意：

• 大多数t.function都会有一个参数out=None,产生的结果将保存在out指定的tensor之中
• t.set_num_threads可以设置PyTorch进行CPU多线程并行计算时所占用的线程，用来限制PyTorch所占用的CPU数目
• t.set_printpotions可以用来设置打印tensor时的数值精度和格式

下面举例说明：

a = t.arange(0,32769).short() #int16(-32768 ~ 32767)
print(a.dtype)
print(a[-1],a[-2])#16bit的IntTensor精度有限导致溢出
b = t.IntTensor()
t.arange(0,32769,out=b)#32bit的LongTensor就不会导致溢出了
b[-1],b[-2]

返回：

torch.int16
tensor(-32768, dtype=torch.int16) tensor(32767, dtype=torch.int16)
Out[10]:
(tensor(32768, dtype=torch.int32), tensor(32767, dtype=torch.int32))

 

a = t.randn(2,3)
a

返回：

tensor([[ 0.2182, -1.1149,  1.1781],
        [ 1.0245,  0.9339,  1.6028]])

设置精度：

t.set_printoptions(precision=10)#将精度设为10
a

返回：

tensor([[ 0.2181526423, -1.1149182320,  1.1780972481],
        [ 1.0244952440,  0.9339445829,  1.6027815342]])

 

13.小试牛刀——线性回归

线性回归利用数理统计中的回归分析来确定两种或两种以上变量之间相互依赖的定量关系，其表达式为y=wx +b +e,误差e服从均值为0的正态分布。线性回归的损失函数是：

利用随机梯度下降法更新参数w,b来最小化损失函数，最终学习得到w,b的数值

导入需要的包：

import torch as t
from matplotlib import pyplot as plt
from IPython import display

生成训练数据：

#设置随机数种子，保证在不同计算机上运行时下面的输出一致
t.manual_seed(1000)
def get_fake_data(batch_size=8):
    '''产生随机数据：y=x*2+3,加上了些噪音点'''
    x = t.rand(batch_size, 1)*20 #生成size为(batch_size, 1)的二维数组，并元素乘20
    y = x * 2 + (1+t.rand(batch_size, 1))*3 #用于生成噪音
    return x,y

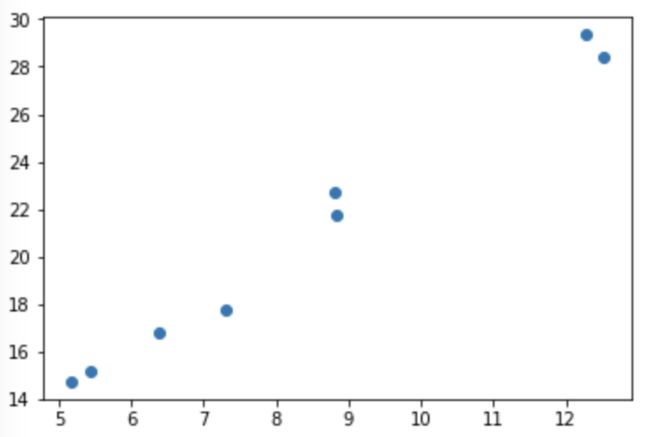
测试看看会生成什么样的数据：

#来看看产生的x-y分布，输出如图所示
x, y = get_fake_data()
plt.scatter(x.squeeze().numpy(), y.squeeze().numpy())

图示为：

生成参数：

#随机初始化参数
w = t.rand(1,1)
b = t.zeros(1,1)

实现：

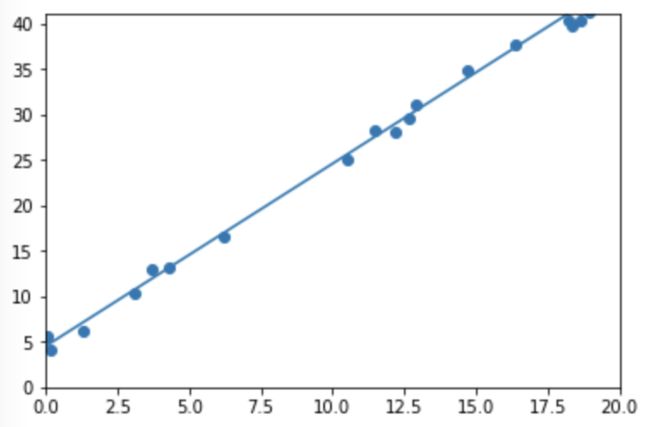
lr = 0.001 #学习率

for ii in range(2000): #2000次迭代
    x, y = get_fake_data() #生成数据
    
    #前向传播forward，计算loss
    y_pred = x.mm(w) + b.expand_as(y)
    loss = 0.5*(y_pred - y)**2 #均方误差就loss
    loss = loss.sum()
    
    #backward:手动计算梯度
    dloss = 1
    dy_pred = dloss *(y_pred - y)
    
    
    dw = x.t().mm(dy_pred)
    db = dy_pred.sum()
    
    #更新参数
    w.sub_(lr * dw)
    b.sub_(lr * db)
    
    if ii%1000 == 0:#没1000次迭代，画一次图
        #画图
        display.clear_output(wait=True)
        x = t.arange(0, 20).view(-1,1).float()
        y = x.mm(w) + b.expand_as(x)
        plt.plot(x.numpy(), y.numpy()) #预测
        
        x2, y2 = get_fake_data(batch_size=20)
        plt.scatter(x2.numpy(), y2.numpy())
        
        plt.xlim(0, 20)        
        plt.ylim(0, 41)
        plt.show()
        plt.pause(0.5)
    

print(w.squeeze(),b.squeeze())

返回：

tensor(1.9801) tensor(4.5172)

上面得到的是学习到的w,b的值，看下面的图可以看见直线和数据很好地实现了拟合

图示为： 

 

转载于:https://www.cnblogs.com/wanghui-garcia/p/10617338.html