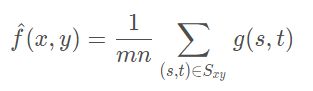Python3+OpenCV（十一）：空间域滤波复原

---

---

空间域滤波复原 是在已知 噪声模型 的基础上，对噪声的空间域滤波

主要包括 ：

• 均值滤波器 (算术均值滤波器、几何均值滤波器、谐波均值滤波器、逆谐波均值滤波器)
• 顺序统计滤波器 (中值滤波器、二维中值滤波器、修正后的阿尔法均值滤波器、最大/最小滤波器、中点滤波器)

1、均值滤波器

采用均值滤波模板对图像噪声进行滤除。
Sxy：表示滤波器的卷积核移动到某位置后与图像重合的区域
m,n：表示滤波器卷积核的尺寸(m x n)

(1) 算术均值滤波器

算术均值滤波器可以降低噪声，但是对椒盐噪声效果不好。

因为均值滤波将区域内所有像素进行求和取均值，这些像素中就包含了椒盐过亮或过暗的噪声，对均值的影响较大，所以滤波效果不好。

另外，均值滤波器是对某个区域内像素取均值来代替当前位置像素，所以图像会更加平滑，也就是会模糊化。

(2) 几何均值滤波器

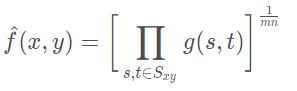
几何均值滤波器相比于算术均值滤波器来说，丢失的图像信息更少。

(3) 谐波均值滤波器

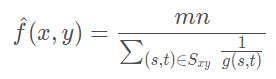
谐波均值滤波器善于处理高斯噪声一类噪声。对盐粒噪声处理效果好，但不适用于对胡椒噪声的处理。

(4) 逆谐波均值滤波器

其中，Q称为滤波器的阶数，这种滤波器适合减少或是在实际中消除椒盐噪声的影响。

当Q为正数时，适合消除胡椒噪声；
当Q为负数时，适合消除盐粒噪声，但无法同时消除两种噪声；
当Q=0时，退化为算术均值滤波器；
当Q=-1时，退化为谐波均值滤波器。

(5) Python实现

实现部分参考了其它博客的代码，找了个比较容易理解，主要就是实现滤波器函数，但是时间复杂度应该挺高的。谐波均值滤波器和逆谐波均值滤波器这两个还没太懂，之后有机会再看看吧。

import cv2
import numpy as np

# 算术均值滤波器
def ArithmeticMean(img, kernelSize):
    AImg = np.zeros(img.shape)
    k = int((kernelSize-1)/2) # 模板中心

    for i in range(img.shape[0]):
        for j in range(img.shape[1]):
            # 不在滤波核范围内
            if i<k or i>(img.shape[0]-k-1) or j<k or j>(img.shape[1]-k-1):
                AImg[i][j] = img[i][j] # 像素值不变
            else: # 范围内
                for n in range(kernelSize):
                    for m in range(kernelSize):
                        # 范围内像素值求和取平均
                        AImg[i][j] += 1.0/(kernelSize*kernelSize)*img[i-k+n][j-k+m]

    AImg = np.uint8(AImg)
    return AImg

# 几何均值滤波器
def GeometricMean(img, kernelSize):
    GImg = np.ones(img.shape)
    k = int((kernelSize-1)/2) # 模板中心

    for i in range(img.shape[0]):
        for j in range(img.shape[1]):
            # 不在滤波核范围内
            if i<k or i>(img.shape[0]-k-1) or j<k or j>(img.shape[1]-k-1):
                GImg[i][j] = img[i][j] # 像素值不变
            else: # 范围内
                for n in range(kernelSize):
                    for m in range(kernelSize):
                        # 范围内像素值求乘积后开根号
                        GImg[i][j] *= img[i-k+n][j-k+m]
                GImg[i][j] = pow(GImg[i][j], 1/(kernelSize*kernelSize))

    GImg = np.uint8(GImg)
    return GImg

# 谐波均值滤波器
def HarmonicMean(img, kernelSize):
    HImg = np.zeros(img.shape)
    k = int((kernelSize-1)/2)

    for i in range(img.shape[0]):
        for j in range(img.shape[1]):
            # 不在滤波核范围内
            if i<k or i>(img.shape[0]-k-1) or j<k or j>(img.shape[1]-k-1):
                HImg[i][j] = img[i][j] # 像素值不变
            else:
                for n in range(kernelSize):
                    for m in range(kernelSize):
                        if all(img[i-k+n][j-k+m]) == 0:
                            HImg[i][j] = 0
                            break
                        else:
                            HImg[i][j] += 1/img[i-k+n][j-k+m]
                    else:
                        continue
                    break

                if all(HImg[i][j]) != 0:
                    HImg[i][j] = (kernelSize*kernelSize)/HImg[i][j]

    HImg = np.uint8(HImg)
    return HImg

# 逆谐波均值滤波器
def IHarmonicMean(img, kernelSize, Q):
    IHImg = np.zeros(img.shape)
    # print(IHImg)
    # print(img[0][0])
    k = int((kernelSize-1)/2)

    for i in range(img.shape[0]):
        for j in range(img.shape[1]):
            # 不在滤波核范围内
            if i<k or i>(img.shape[0]-k-1) or j<k or j>(img.shape[1]-k-1):
                IHImg[i][j] = img[i][j] # 像素值不变
            else:
                res_top = 0
                res_bottom = 0
                for n in range(kernelSize):
                    for m in range(kernelSize):
                        if Q>0:
                            res_top += pow(img[i-k+n][j-k+m], Q+1)
                            res_bottom += pow(img[i-k+n][j-k+m], Q)
                # print(res_top)
                        else:
                            if all(img[i-k+n][j-k+m]) == 0:
                                IHImg[i][j] = 0
                                break
                            else:
                                res_top += pow(img[i-k+n][j-k+m], Q+1)
                                res_bottom += pow(img[i-k+n][j-k+m], Q)
                    else:
                        continue
                    break
                else:
                    if all(res_bottom) != 0:
                        IHImg[i][j] = res_top/res_bottom

    HImg = np.uint8(IHImg)
    return HImg

img = cv2.imread('D:\Study\digital image processing/lena1.jpg')
cv2.imshow("img", img)
# res1 = ArithmeticMean(img, 3)
# cv2.imshow("AImg", res1)
# res2 = GeometricMean(img, 3)
# cv2.imshow("GImg", res2)
# res3 = HarmonicMean(img, 3)
# cv2.imshow("HImg", res3)
# res4 = IHarmonicMean(img, 3, -1.5)
# cv2.imshow("Q=-1.5", res4)
# res5 = IHarmonicMean(img, 3, 1.5)
# cv2.imshow("Q=1.5", res5)

cv2.waitKey(0)
cv2.destroyAllWindows()

算术均值滤波

几何均值滤波

谐波均值滤波

逆谐波均值滤波器

2、顺序统计滤波器

(1) 中值滤波器

即取滤波器覆盖范围内所有像素的中位数。中值滤波可去掉椒盐噪声，平滑效果优于均值滤波，在抑制随机噪声的同时也能保持图像边缘少受模糊。

(2) 修正后的阿尔法均值滤波器

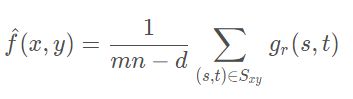
假设在Sxy邻域内去掉gr(s,t)最高的d/2个灰度值和最低的d/2个灰度值后，剩下的mn-d个灰度值用gr(s,t)来代替，即可得到上式。

其中d的取值范围为[0,mn-1]。

当d=0时，退化成算术均值滤波器；
当d=mn-1时，退化成中值滤波器；
当d为其他值时，适合处理混合多种噪声的情况，如高斯噪声和椒盐噪声混合的情况。

(3) 最大/最小滤波器

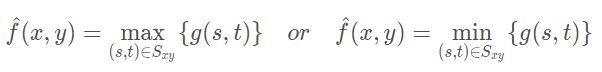
最大值滤波器适合处理胡椒噪声，但会从黑色物体边缘移走一些黑色像素；最小值滤波器适合处理盐粒噪声，但会从亮色物体边缘移走一些白色像素。

(4) 中点滤波器

计算最大值和最小值的中点。中点滤波器适用于处理随机分布的噪声，如高斯噪声或均匀噪声，但不太适合处理椒盐噪声。

(5) Python实现

中值滤波器

import cv2
import numpy as np

# 方法一
# 调用 medianBlur() 函数实现中值滤波
img = cv2.imread('D:\Study\digital image processing/lena2.jpg')
#常用来去除椒盐噪声
#卷积核使用奇数
res = cv2.medianBlur(img, 3)
cv2.imshow("Input", img)
cv2.imshow("Median", res)
cv2.waitKey()
cv2.destroyAllWindows()

# 方法二
# 填充方式是无填充
# 对图像边缘，上下左右处忽略掉不进行滤波，只对可以容纳下一个滤波模板的区域滤波
# def MedianFilter(image, k=3, padding=None):
#     img = image
#     height = img.shape[0]
#     width = img.shape[1]
#     if not padding:
#         edge = int((k-1)/2)
#         if height-1-edge <= edge or width-1-edge <= edge:
#             print("The parameter k is to large.")
#             return None
#         res = np.zeros((height, width), dtype="uint8")
#         for i in range(edge, height-edge):
#             for j in range(edge, width-edge):
#                 # 调用np.median求取中值
#                 res[i, j] = np.median(img[i-edge:i+edge+1, j-edge:j+edge+1])
#     return res
# 
# img = cv2.imread('D:\Study\digital image processing/lena2.jpg')
# res = MedianFilter(img)
# cv2.imshow("Input", img)
# cv2.imshow("Median", res)
# cv2.waitKey()
# cv2.destroyAllWindows()

最大/最小/中点滤波器可以用类似的方法，使用最大值/最小值/中点值来代替中心值。

参考博客
https://blog.csdn.net/weixin_41424926/article/details/101630462
https://blog.csdn.net/weixin_42453126/article/details/106417455