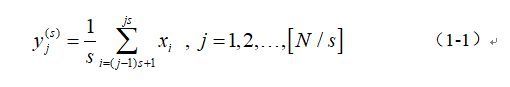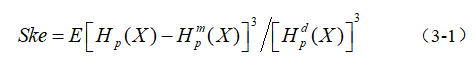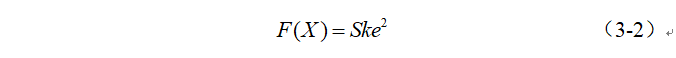参数优化多尺度排列熵算法
目录
一、多尺度排列熵原理
1.1 排列熵（PE）
1.2 多尺度排列熵（MPE）
1.3 参数对MPE的影响
二、参数优化方法
2.1 遗传算法（GA）
2.2 粒子群优化算法（PSO）
2.3 多作用力粒子群优化算法（MFPSO）
三、多尺度排列熵参数优化
3.1 适应度函数的确定
3.2 参数优化过程
四、MATLAB源代码
参考文献
一、多尺度排列熵原理
1.1 排列熵（PE）
排列熵算法原理及MATLAB代码见地址：排列熵、模糊熵、近似熵、样本熵的原理及MATLAB实现
排列熵只能检测时间序列在单一尺度上的复杂性和随机性。复杂系统的输出时间序列在多重尺度上包含特征信息，为研究时间序列的多尺度复杂性变化，排列熵分析不再满足。
1.2 多尺度排列熵（MPE）
对长度为 
的时间序列
进行粗粒化处理得到粗粒化序列
，其表达式为：
其中，
为尺度因子，
。![[N/s]](http://img.e-com-net.com/image/info8/428d16f5cf2d41ca9b4b1f43d35e6396.gif){kind=small}
表示对 N/s 取整，当 =1 时，粗粒化序列即为原始序列。
对每个粗粒化序列，计算其排列熵即可得到多尺度排列熵。多尺度排列熵的计算流程如图1所示，具体步骤如下：
（1）将时间序列粗粒化处理；
（2）对每个粗粒化序列相空间重构；
（3）重构分量按升序排列，计算每一种符号序列出现的概率；
（4）根据式（1-1）计算每个粗粒化序列的排列熵，并进行归一化处理，进而得到多尺度排列熵值。
图1 多尺度排列熵计算流程
1.3 参数对MPE的影响
在粗粒化环节中，尺度因子的选择尤为重要，若尺度因子 取值过小，则不能最大限度的提取信号的特征信息；若 取值过大，将有可能造成信号之间的复杂度差异被抹除。同时，在多尺度排列熵的计算过程中，若嵌入维数 
取值太小，算法的突变检测性能降低；若嵌入维数 取值太大，将无法反应时间序列的细微变化。而且，时间序列长度 与延迟时间 
对多尺度排列熵算法也有着不同的影响。
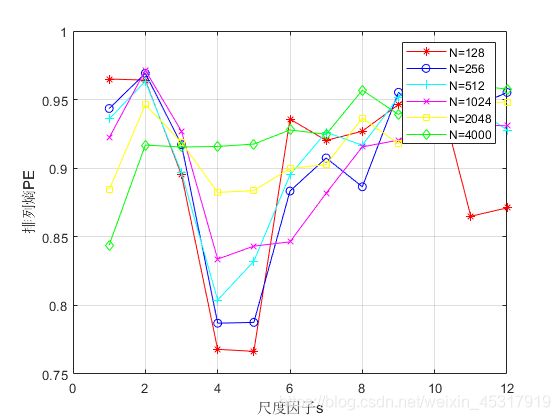
计算不同长度信号在不同嵌入维数m下的MPE值，如图 2(a)~2(d)所示。
图2(a) 嵌入维数m=3
图2(b) 嵌入维数m=4
图2(c) 嵌入维数m=5
图2(d) 嵌入维数m=6
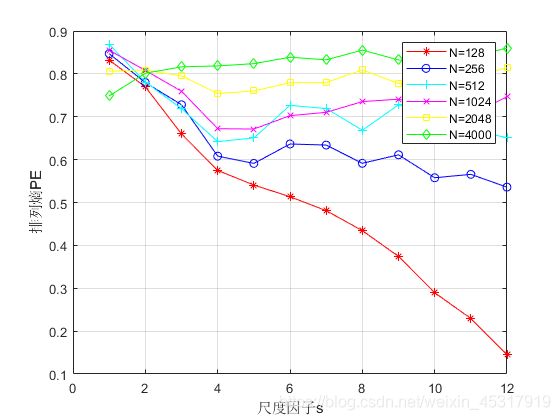
信号长度N=1024，嵌入维数m=6，尺度因子s=12，如图 3 所示为计算信号在不同延迟时间 t 值下的MPE值。
图3 不同延迟时间 t 下的 MPE
信号长度N=1024，嵌入维数m=6，延迟时间t=2，如图 4 所示为计算信号在不同尺度因子s下的MPE值。
图4 不同尺度因子 s 下的 MPE
二、参数优化方法
2.1 遗传算法（GA）
遗传算法的原理及MATLAB代码见地址：遗传算法原理（含详细注释的MATLAB代码）
https://www.jianshu.com/p/8a965c04c787#Github上的MATLAB代码（可直接下载）https://github.com/Shuai-Xie/genetic-algorithm
遗传算法的流程如图5所示。
图5 GA 算法流程图
2.2 粒子群优化算法（PSO）
粒子群优化算法的原理及MATLAB代码见地址：PSO-LSSVM算法及其MATLAB代码
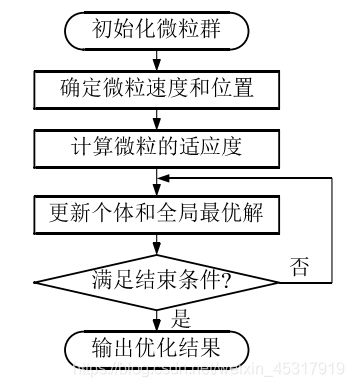
粒子群优化算法的流程如图6所示。
图6 PSO 算法流程图
2.3 多作用力粒子群优化算法（MFPSO）
多作用力粒子群优化（Multi Force Particle Swarm Optimization，MFPSO）算法是对PSO 算法的改进，是一种阶段性搜索算法。该算法通过增加粒子间的引力、斥力等作用力构造规则，形成前期、中期和后期三个搜索阶段，使算法的搜索能力与收敛速度得到提高。
三、多尺度排列熵参数优化
3.1 适应度函数的确定
为分析一组数据的总体趋势，通过求其均值，可以观察数据的集中趋势。但仅凭均值并不能够完全表征一组数据的总体概况，此时可以求取数据的偏度。偏度绝对值越大，表明均值的效能越有问题，偏度绝对值越小，则均值越可信赖。为此，本文选用多尺度排列熵偏度的平方函数作为目标函数，求其最小值。
偏度表征的是概率密度为非正态分布的随机序列偏离正态分布的程度，是统计数据分布非对称程度的数字特征。其中，偏度为零，表示对称分布；偏度大于零，表示不对称部分的分布更趋向正值；偏度小于零，表示不对称部分的分布更趋向负值。
将时间序列所有尺度下的排列熵组成序列
，通过式（3-1）计算其偏度Ske：
其中，
为序列 
的均值；
为 序列的标准差；
为求序列的期望。
目标函数为：
3.2 参数优化过程
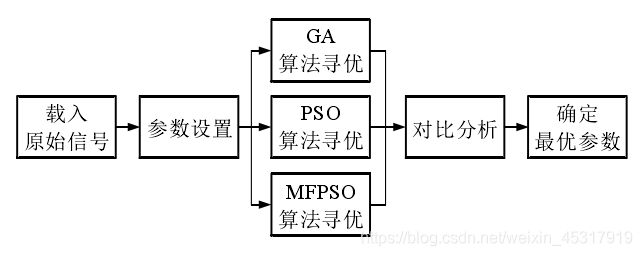
多尺度排列熵的参数优化流程如图8所示，具体过程如下：
（1）载入原始信号，设置各个优化算法的参数，初始化多尺度排列熵算法的参数；
（2）由式(3-17)及式(3-18)求适应度函数，分别利用GA、PSO和MFPSO对 MPE 的参数进行优化，得到 3 组优化参数；
（3）对 3 组优化参数进行对比分析，进而确定 MPE 的最优参数。
图8 MPE 参数优化流程图
四、MATLAB源代码
遗传算法(GA)、粒子群优化算法(PSO)对多尺度排列熵算法(MPE)的参数进行寻优，得到最优参数，代码地址如下：参数优化多尺度排列熵
参考文献
[1]张运东. 基于 FVMD 多尺度排列熵和 GK 模糊聚类的故障诊断方法[D]. 秦皇岛：燕山大学, 32-45.
[2]陈东宁, 张瑞星, 姚成玉, 等. 求解液压阀块加工车间调度的多作用力微粒群算法[J]. 中国机械工程, 2015, 26(3): 369-378.
多尺度排列熵算法的提出者：Aziz W, Arif M. Multiscale permutation entropy of physiological times series[C]//Proceeding of IEEE International Multi-topic Conference, INMIC, 2005: 1-6.