深度学习常用的激活函数以及python实现(Sigmoid、Tanh、ReLU、Softmax、Leaky ReLU、ELU、PReLU、Swish、Squareplus)

2022.05.26更新

1. 增加SMU激活函数

前言

激活函数是一种添加到人工神经网络中的函数，类似于人类大脑中基于神经元的模型，激活函数最终决定了要发射给下一个神经元的内容。

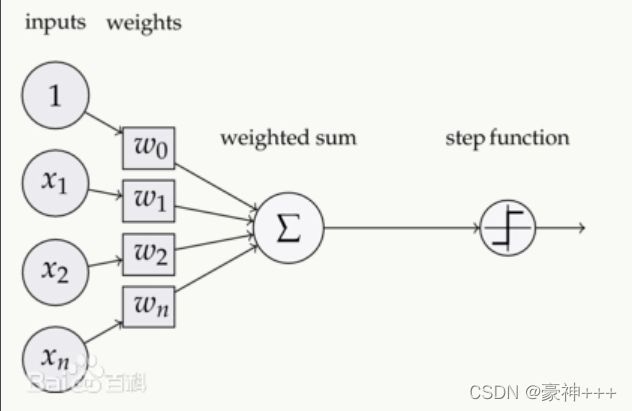
此图来自百度百科，其中step function就是激活函数，它是对之前一层进行汇总后信号进行激活，传给下一层神经元。
常用的激活函数有以下10个：

常用的10个激活函数

1. Sigmoid
2. Tanh
3. ReLU
4. Softmax
5. Leaky ReLU
6. ELU
7. PReLU
8. Swish
9. Squareplus
10. SMU

1. Sigmoid

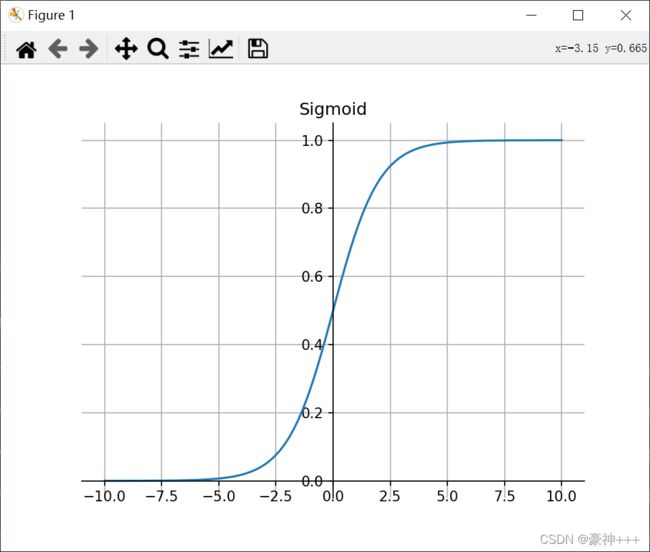
如上图是Sigmoid函数的函数图像。

Sigmoid 函数的图像看起来像一个 S 形曲线。

公式：
            $f(x)=\frac{1}{1+e^{-x}}$
特点：

1. Sigmoid 函数的输出范围是 0 到 1。由于输出值在 0 到 1，所以它可以对每个神经元的输出进行了归一化。
2. 因为Sigmoid 函数的输出范围是 0 到 1，所以可以用于将预测概率作为输出的模型。
3. 梯度平滑，避免跳跃的输出值。
4. 容易梯度消失。
5. 函数输出不是以 0 为中心的，这会降低权重更新的效率。
6. Sigmoid 函数是指数运算，计算机运行得较慢。

代码演示：

import matplotlib.pyplot as plt
import numpy as np

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

fig, ax = plt.subplots()

x = np.linspace(-10, 10, 100)
y = sigmoid(x)

ax.plot(x, y)
# 画轴
ax.spines['top'].set_color('none')
ax.spines['right'].set_color('none')

ax.spines['bottom'].set_position(('data', 0))
ax.spines['left'].set_position(('axes', 0.5))
plt.grid() # 设置方格
plt.title("Sigmoid")
plt.show()

2. Tanh

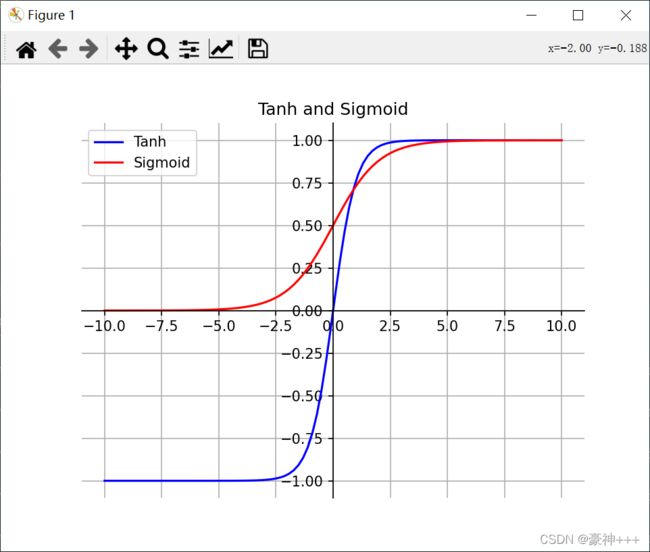
如上图是Tanh函数的函数图像。

Tanh 函数的图像看起来像一个有点扁的 S 形曲线。Tanh 是一个双曲正切函数。Tanh 函数和 Sigmoid 函数的曲线相对相似。但是它比 Sigmoid 函数更有一些优势。

公式：
            $f(x)=\frac{2}{1+e^{-2x}}-1$
特点：

1. 首先，当输入较大或较小时，输出几乎是平滑的并且梯度较小，这不利于权重更新。二者的区别在于输出间隔，Tanh 的输出间隔为 1，并且整个函数以 0 为中心，比 Sigmoid 函数更好。
2. 在 Tanh 图中，负数信号输入，输出也是负数信号。
3. 在一般的二元分类问题中，Tanh 函数用于隐藏层，而 Sigmoid 函数用于输出层，但这并不是固定的，需要根据特定问题进行调整。
   代码演示：

import matplotlib.pyplot as plt
import numpy as np

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

def tanh(x):
    return 2 / (1 + np.exp(-2*x)) - 1

fig, ax = plt.subplots()

x = np.linspace(-10, 10, 100)
y1 = tanh(x)

y2 = sigmoid(x)

ax.plot(x, y1, '-b', label='Tanh')
ax.plot(x, y2, '-r', label='Sigmoid')
ax.legend() # 设置图例
# 画轴
ax.spines['top'].set_color('none')
ax.spines['right'].set_color('none')

ax.spines['bottom'].set_position(('data', 0))
ax.spines['left'].set_position(('axes', 0.5))
plt.grid() # 设置方格
plt.title("Tanh and Sigmoid")
plt.show()

3. ReLU

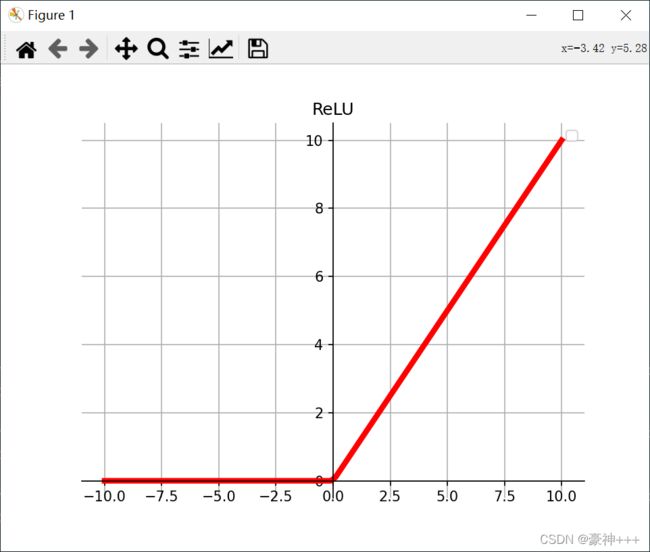
如上图是ReLU函数的函数图像。

ReLU 函数是深度学习中较为流行的一种激活函数。

公式：
        $f(x)=\{\begin{array}{ll}max(0,x)& \text{x ≥ 0}\\ 0& \text{x < 0}\end{array}$
特点：

1. 当输入为正时，不存在梯度饱和问题。
2. 计算速度快。ReLU 函数中只存在线性关系，因此它的计算速度比 sigmoid 和 tanh 更快。
3. 当输入为负时，ReLU 完全失效，在正向传播过程中，这不是问题。有些区域很敏感，有些则不敏感。但是在反向传播过程中，如果输入负数，则梯度将完全为零。
   代码演示：

import matplotlib.pyplot as plt
import numpy as np

def relu(x):
    return np.maximum(0, x)

fig, ax = plt.subplots()

x = np.linspace(-10, 10, 100)
y = relu(x)
ax.plot(x, y, '-r', linewidth=4)
ax.legend() # 设置图例
# 画轴
ax.spines['top'].set_color('none')
ax.spines['right'].set_color('none')

ax.spines['bottom'].set_position(('data', 0))
ax.spines['left'].set_position(('axes', 0.5))
plt.grid() # 设置方格
plt.title("ReLU")
plt.show()

4. Softmax

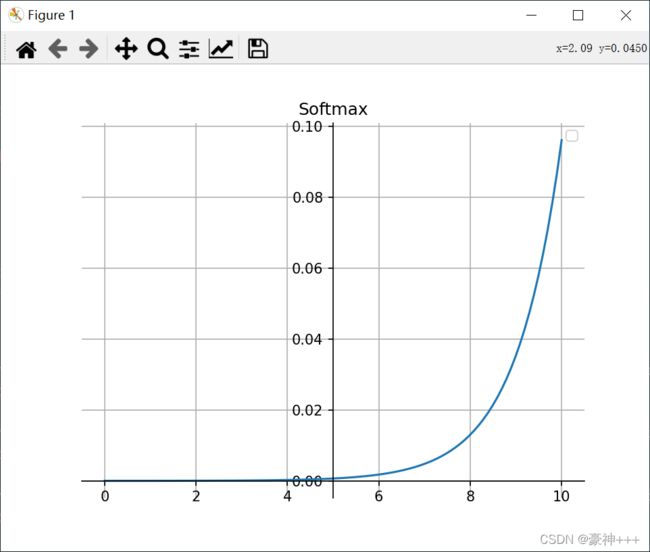
如上图是Softmax函数的函数图像。

公式：
                   $\frac{e^{x_i}}{{\sum }_{j=1}^n{e}^{x_j}}$
特点：

1. 在零点不可微。
2. 负数信号输入的梯度为零，这意味着对于该区域的激活，权重不会在反向传播期间更新，因此会产生永不激活的死亡神经元。
3. Softmax 函数的分母结合了原始输出值的所有因子，这意味着 Softmax 函数获得的各种概率彼此相关，因此Softmax 是用于多类分类问题。

代码演示

import matplotlib.pyplot as plt
import numpy as np

def softmax(x):
    x = np.exp(x) / np.sum(np.exp(x))
    return x
fig, ax = plt.subplots()

x = np.linspace(-10, 10, 100)
y = softmax(x)
ax.plot(x, y)
ax.legend() # 设置图例
# 画轴
ax.spines['top'].set_color('none')
ax.spines['right'].set_color('none')

ax.spines['bottom'].set_position(('data', 0))
ax.spines['left'].set_position(('axes', 0.5))
plt.grid() # 设置方格
plt.title("Softmax")
plt.show()

5. Leaky ReLU

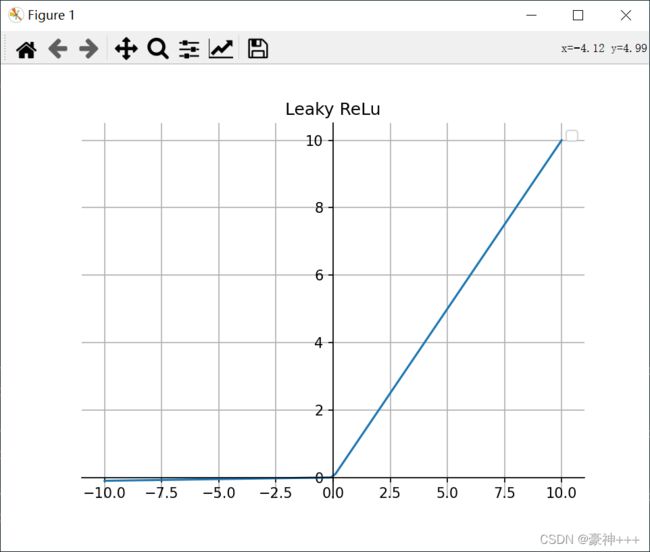
如上图是Leaky ReLU函数的函数图像。

它是一种专门设计用于解决 ReLU 梯度消失问题的激活函数。

公式：
          $f(x)=\{\begin{array}{ll}x& \text{x ≥ 0}\\ ax& \text{x < 0}\end{array}$
特点：

1. Leaky ReLU 通过把 x 的非常小的线性分量给予负数信号来调整负值的零梯度问题。
2. leak 有助于扩大 ReLU 函数的范围，通常 a 的值为 0.01 左右。

注意： 从理论上讲，Leaky ReLU 具有 ReLU 的所有优点，而且 Dead ReLU 不会有任何问题，但在实际操作中，尚未完全证明 Leaky ReLU 总是比 ReLU 更好。

代码演示：

import matplotlib.pyplot as plt
import numpy as np

def leaky_relu(x,a=0.01):
    return np.maximum(a*x, x)
    
fig, ax = plt.subplots()

x = np.linspace(-10, 10, 100)
y = leaky_relu(x)
ax.plot(x, y)
ax.legend() # 设置图例
# 画轴
ax.spines['top'].set_color('none')
ax.spines['right'].set_color('none')

ax.spines['bottom'].set_position(('data', 0))
ax.spines['left'].set_position(('axes', 0.5))
plt.grid() # 设置方格
plt.title("Leaky ReLu")
plt.show()

6. ELU

如上图是ELU函数的函数图像。

ELU 的提出也解决了 ReLU 的问题。与 ReLU 相比，ELU 有负值，这会使激活的平均值接近零。均值激活接近于零可以使学习更快，因为它们使梯度更接近自然梯度。

公式：
        $f(x)=\{\begin{array}{ll}x& \text{x ≥ 0}\\ \alpha (e^x-1)& \text{x < 0}\end{array}$
特点：

1. ELU 通过减少偏置偏移的影响，使正常梯度更接近于单位自然梯度，从而使均值向零加速学习。
2. ELU 在较小的输入下会饱和至负值，从而减少前向传播的变异和信息。

注意： 它的计算强度更高。与 Leaky ReLU 类似，尽管理论上比 ReLU 要好，但目前在实践中没有充分的证据表明 ELU 总是比 ReLU 好。

代码演示：

import matplotlib.pyplot as plt
import numpy as np
    
def elu(x,alpha=1):
    a = x[x>0]
    b = alpha*(np.exp(x[x<0])-1)
    result=np.concatenate((b,a),axis=0)
    return result

fig, ax = plt.subplots()

x = np.linspace(-10, 10, 100)
y = elu(x)
ax.plot(x, y)
ax.legend() # 设置图例
# 画轴
ax.spines['top'].set_color('none')
ax.spines['right'].set_color('none')

ax.spines['bottom'].set_position(('data', 0))
ax.spines['left'].set_position(('axes', 0.5))
plt.grid() # 设置方格
plt.title("ELU")
plt.show()

7. PReLU

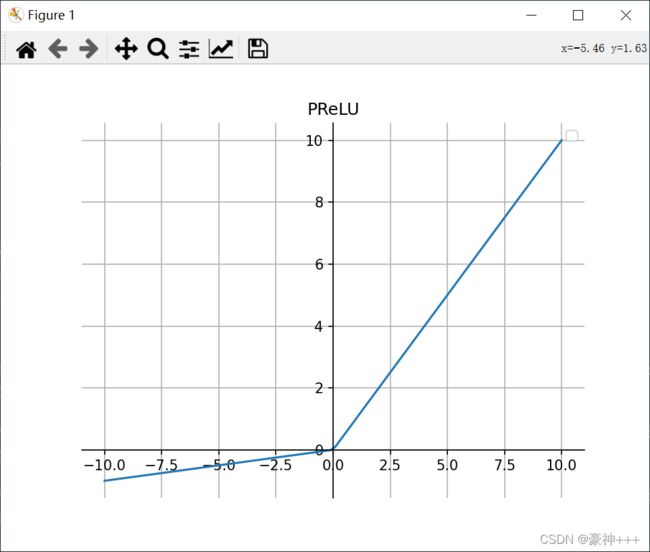
PReLU 也是 ReLU 的改进版本。

公式：
          $f(x)=\{\begin{array}{ll}x& \text{x ≥ 0}\\ \alpha x& \text{x < 0}\end{array}$
若$\alpha$是可学习的参数，则 $f(x)$变为 PReLU。
特点：

1. 与 ELU 相比，PReLU 在负值域是线性运算。尽管斜率很小，但不会趋于 0。

代码就不演示了，和上面得Leaky ReLU一样。

8. Swish

如上图是Swish函数的函数图像。

Swish 的设计受到了 LSTM 和高速网络中 gating 的 sigmoid 函数使用的启发。我们使用相同的 gating 值来简化 gating 机制，这称为 self-gating。

self-gating 的优点在于它只需要简单的标量输入，而普通的 gating 则需要多个标量输入。这使得诸如 Swish 之类的 self-gated 激活函数能够轻松替换以单个标量为输入的激活函数（例如 ReLU），而无需更改隐藏容量或参数数量。

公式：
              $y=x\ast sigmoid(x)$
特点：

1. 无界性有助于防止慢速训练期间，梯度逐渐接近 0 并导致饱和；（同时，有界性也是有优势的，因为有界激活函数可以具有很强的正则化，并且较大的负输入问题也能解决）。
2. 导数恒大于零。
3. 平滑度在优化和泛化中起了重要作用。

代码演示：

import matplotlib.pyplot as plt
import numpy as np

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

def swish(x):
    return sigmoid(x) * x

fig, ax = plt.subplots()

x = np.linspace(-10, 10, 100)
y = swish(x)
ax.plot(x, y)
ax.legend() # 设置图例
# 画轴
ax.spines['top'].set_color('none')
ax.spines['right'].set_color('none')

ax.spines['bottom'].set_position(('data', 0))
ax.spines['left'].set_position(('axes', 0.5))
plt.grid() # 设置方格
plt.title("Swish")
plt.show()

9. Squareplus

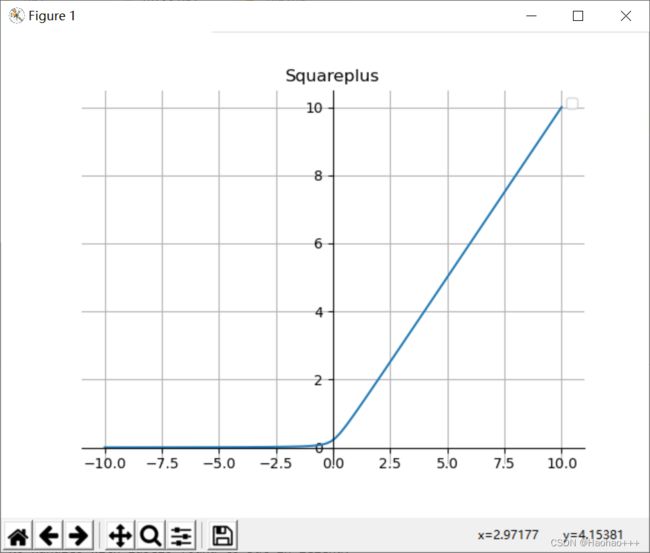
如上图是Squareplus函数的函数图像。

Squareplus是Softplus优化版本，Squareplus由超参数b>0定义，它决定了x=0附近弯曲区域的大小。
公式：
              $y=\frac{1}{2}(x+\sqrt{x^2+b})$
特点：

1. 它的输出是非负的。
2. 它是ReLU的一个上界函数，会随着|x|的增长而接近ReLU。
3. 它是连续的。
4. Squareplus只使用代数运算进行计算，这使得它非常适合计算资源或指令集有限的情况。此外，当x较大时，Squareplus无需特别考虑确保数值稳定性。

代码演示：

import numpy as np
import matplotlib.pyplot as plt

def Squareplus(x, b=0.2):
    x = 0.5 * (x + np.sqrt(x**2+b))
    return x

fig, ax = plt.subplots()

x = np.linspace(-10, 10, 100)
y = Squareplus(x)
ax.plot(x, y)
ax.legend() # 设置图例
# 画轴
ax.spines['top'].set_color('none')
ax.spines['right'].set_color('none')

ax.spines['bottom'].set_position(('data', 0))
ax.spines['left'].set_position(('axes', 0.5))
plt.grid() # 设置方格
plt.title("Squareplus")
plt.show()

10. SMU

该函数是在已知激活函数Leaky ReLU近似的基础上，提出了一种新的激活函数，称之为Smooth Maximum Unit(SMU)。用SMU替换ReLU，ShuffleNet V2模型在CIFAR100数据集上得到了6.22%的提升。

参考：https://github.com/iFe1er/SMU_pytorch

tensorflow2.x代码如下：

import tensorflow as tf

def SMU(x,alpha=0.25):
    mu = tf.compat.v1.get_variable('SMU_mu', shape=(),
                       initializer=tf.constant_initializer(1000000),
                       dtype=tf.float32)
    return ((1+alpha)*x + (1-alpha)*x*tf.math.erf(mu*(1-alpha)*x))/2

def SMU1(x,alpha=0.25):
    mu = tf.compat.v1.get_variable('SMU1_mu', shape=(),
                       initializer=tf.constant_initializer(4.352665993287951e-9),
                       dtype=tf.float32)
    return ((1+alpha)*x+tf.math.sqrt(tf.math.square(x-alpha*x)+tf.math.square(mu)))/2

pytorch代码如下：

import torch
from torch import nn

class SMU(nn.Module):
    '''
    Implementation of SMU activation.
    Shape:
        - Input: (N, *) where * means, any number of additional
          dimensions
        - Output: (N, *), same shape as the input
    Parameters:
        - alpha: hyper parameter
    References:
        - See related paper:
        https://arxiv.org/abs/2111.04682
    Examples:
        >>> smu = SMU()
        >>> x = torch.Tensor([0.6,-0.3])
        >>> x = smu(x)
    '''
    def __init__(self, alpha = 0.25):
        '''
        Initialization.
        INPUT:
            - alpha: hyper parameter
            aplha is initialized with zero value by default
        '''
        super(SMU,self).__init__()
        self.alpha = alpha
        # initialize mu
        self.mu = torch.nn.Parameter(torch.tensor(1000000.0)) 
        
    def forward(self, x):
        return ((1+self.alpha)*x + (1-self.alpha)*x*torch.erf(self.mu*(1-self.alpha)*x))/2
        
        
class SMU1(nn.Module):
    '''
    Implementation of SMU-1 activation.
    Shape:
        - Input: (N, *) where * means, any number of additional
          dimensions
        - Output: (N, *), same shape as the input
    Parameters:
        - alpha: hyper parameter
    References:
        - See related paper:
        https://arxiv.org/abs/2111.04682
    Examples:
        >>> smu1 = SMU1()
        >>> x = torch.Tensor([0.6,-0.3])
        >>> x = smu1(x)
    '''
    def __init__(self, alpha = 0.25):
        '''
        Initialization.
        INPUT:
            - alpha: hyper parameter
            aplha is initialized with zero value by default
        '''
        super(SMU1,self).__init__()
        self.alpha = alpha
        # initialize mu
        self.mu = torch.nn.Parameter(torch.tensor(4.352665993287951e-9)) 
        
    def forward(self, x):
        return ((1+self.alpha)*x+torch.sqrt(torch.square(x-self.alpha*x)+torch.square(self.mu)))/2