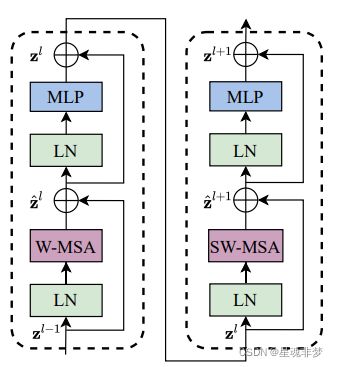
【神经网络架构】Swin Transformer细节详解-2

图1 2个MSA。对应下面depth中的2。

图2 SW-MSA 流程

1. cyclic shift + reverse cyclic shift

图3 cyclic shift， shift_size = 7 // 2 = 3  

depth = [2, 2, 6, 2] # MSA的个数
[SwinTransformerBlock(...,shift_size=0 if (i % 2 == 0) else window_size // 2,...)
for i in range(depth)] # window_size

因此，在上图中， W-MSA 的 shift_size = 0，SW-MSA中mask=self.attn_mask，  shift_size = 7 // 2 = 3。

window_size = 7
shift_size = 7 // 2
'''构造多维张量'''
# x=np.arange(14*14*4*96).reshape(1,14,14,96*4)
x=np.arange(14*14).reshape(14,14)
x=torch.from_numpy(x)
print(x)
if shift_size > 0:
    shifted_x = torch.roll(x, shifts=(-shift_size, -shift_size), dims=(0, 1))
    #shifted_x = torch.roll(x, shifts=(-self.shift_size, -self.shift_size), dims=(1, 2))
    print("---------cyclic shift---------")
else:
    shifted_x = x
print(shifted_x)  

# reverse cyclic shift
if shift_size > 0:
    x = torch.roll(shifted_x, shifts=(shift_size, shift_size), dims=(0, 1))
    print("---------reverse cyclic shift---------")
    print(x)  
else:
    x = shifted_x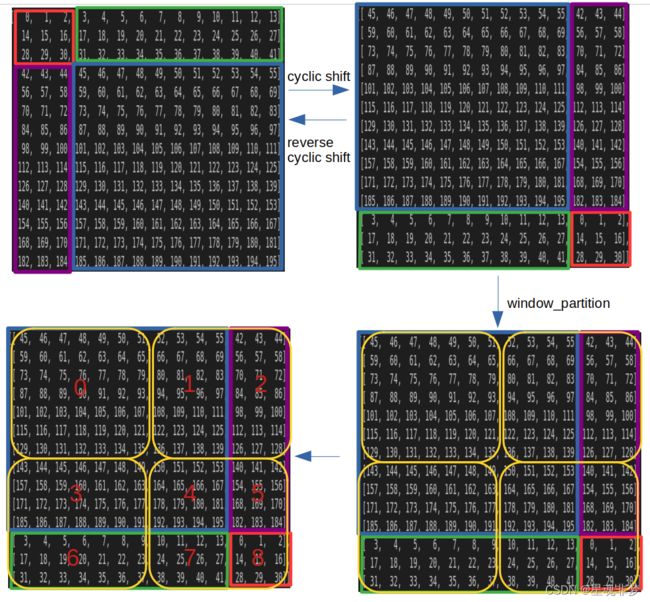

图4 SW具体变化

2. SW-MSA

shift_size = 3
window_size = 7
if shift_size > 0:
    input_resolution = (14, 14)
    # calculate attention mask for SW-MSA
    H, W = input_resolution
    # img_mask = torch.zeros((H, W))  # H W
    img_mask = torch.zeros((1, H, W, 1))  # 1 H W 1
    h_slices = (slice(0, -window_size),
                slice(-window_size, -shift_size),
                slice(-shift_size, None))
    w_slices = (slice(0, -window_size),
                slice(-window_size, -shift_size),
                slice(-shift_size, None))
    cnt = 0
    for h in h_slices:
        for w in w_slices:
            # img_mask[h, w] = cnt
            img_mask[:, h, w, :] = cnt
            cnt += 1
            
    mask_windows = window_partition(img_mask, window_size)  # nW, window_size, window_size ， 这里 nW = 4

    outputs = mask_windows.view(-1, window_size, window_size)
    outputs_1 = torch.stack((outputs[0], outputs[1]), dim=1).view(-1, window_size, window_size*2)
    outputs_2 = torch.stack((outputs[2], outputs[3]), dim=1).view(-1, window_size, window_size*2)
    outputs = torch.stack((outputs_1, outputs_2), dim=1).view(-1, H, W)
    print(outputs)

    mask_windows = mask_windows.view(-1, window_size * window_size) # nW, window_size * window_size
    print(mask_windows)
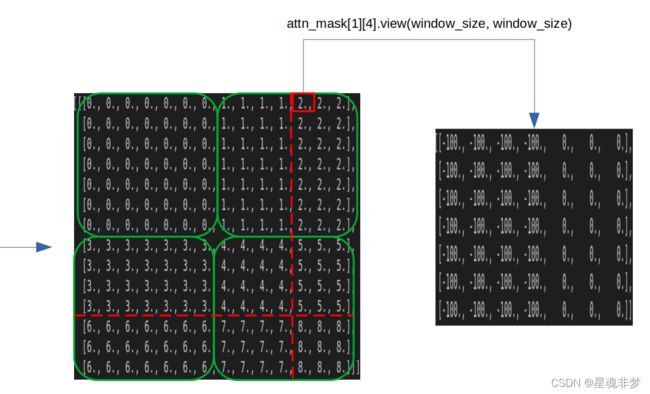
    attn_mask = mask_windows.unsqueeze(1) - mask_windows.unsqueeze(2) # (nW, 1, window_size * window_size) - (nW, window_size * window_size, 1) 
                                                               # 广播 -> (nW, window_size * window_size, window_size * window_size) - (nW, window_size * window_size, window_size * window_size)
    print(attn_mask[1][0] == attn_mask[1][4])
    print(attn_mask[1][4].view(window_size, window_size))
    attn_mask = attn_mask.masked_fill(attn_mask != 0, float(-100.0)).masked_fill(attn_mask == 0, float(0.0)) # 将 非 0 的替换为 -100， 0替换为 0.
    print(attn_mask.shape)

attn_windows = self.attn(x_windows, mask=self.attn_mask) # nW*B, window_size*window_size, C

mask = attn_mask
if mask is not None:
    nW = mask.shape[0] # 一张图被分为多少个windows
    attn = attn.view(B_ // nW, nW, self.num_heads, N, N) + mask.unsqueeze(1).unsqueeze(0) # torch.Size([128, 4, 12, 49, 49]) torch.Size([1, 4, 1, 49, 49]) 广播
    attn = attn.view(-1, self.num_heads, N, N)
    attn = self.softmax(attn)  

使用 attn + mask ， 使得当前位置(如上面 [1][4])，图像中不相邻的区域 -100， 相当于在计算 softmax 时候不考虑这些区域。

3. W-MSA和MSA的复杂度对比 + 4. 整体流程图

         请参考：论文详解：Swin Transformer - 知乎