Python的数据预处理

sklearn.preprocessing 包提供了几个常见的实用功能和变换器类型，用来将原始特征向量更改为更适合机器学习模型的形式。

一般来说，机器学习算法受益于数据集的标准化。如果数据集中存在一些离群值，那么稳定的缩放或转换更合适。不同缩放、转换以及归一在一个包含边缘离群值的数据集中的表现在 Compare the effect of different scalers on data with outliers 中有着重说明。

1、标准化——去均值和方差按比例缩放

标准化（Z-Score），也称去均值和方差按比例缩放。

数据集的 标准化 对scikit-learn中实现的大多数机器学习算法来说是 常见的要求 。如果个别特征或多或少看起来不是很像标准正态分布(具有零均值和单位方差)，那么它们的表现力可能会较差。

在实际情况中,我们经常忽略特征的分布形状，直接经过去均值来对某个特征进行中心化，再通过除以非常量特征(non-constant features)的标准差进行缩放。

例如，在机器学习算法的目标函数(例如SVM的RBF内核或线性模型的l1和l2正则化)，许多学习算法中目标函数的基础都是假设所有的特征都是零均值并且具有同一阶数上的方差。如果某个特征的方差比其他特征大几个数量级，那么它就会在学习算法中占据主导位置，导致学习器并不能像我们说期望的那样，从其他特征中学习。

Python的scikit-learn中有scale和StandardScaler两种方法：

• 公式为：$\frac{(X-mean)}{std}$ 计算时对每个属性/每列分别进行。
• X的shape ：(n_samples, n_features) ，几行代表有几组样本，列表示属性特征。
• 将数据按行属性（按列进行，axis的默认值为axis=0，If 0, independently standardize each feature；若为axis=1则是对每个样本进行标准化，if 1, standardize each sample）减去其均值，并处以其方差。得到的结果是，对于每个属性/每列来说所有数据都聚集在0附近，方差为1。

1.1、scale函数

函数 scale 为数组形状的数据集的标准化提供了一个快捷实现。

使用sklearn.preprocessing.scale()函数，可以直接将给定数据进行标准化。

from sklearn import  preprocessing
import  numpy as  np
#X{array-like, sparse matrix} of shape ：(n_samples, n_features)
X = np.array([[ 1 , - 1 ,  2 ],
              [ 2 ,  0 ,  0 ],
              [ 0 ,  1 , - 1 ]])
X_scaled = preprocessing.scale(X) 
print('标准化的数据：X_scaled=\n',X_scaled)
 
#处理后数据的均值和方差
print('\n处理后数据的均值：X_scaled_mean=',X_scaled.mean(axis= 0 ))
print('处理后数据的标准差：X_scaled_std=',X_scaled.std(axis= 0 ))

对axis=1进行了简单的测试：

1.2、StandardScaler

预处理 模块还提供了一个实用类 StandardScaler ，使用sklearn.preprocessing.StandardScaler类，使用该类的好处在于可以保存****训练集中的参数（均值、方差）直接使用其对象转换测试集数据。

from sklearn import  preprocessing
import  numpy as  np
X = np.array([[ 1 , - 1 ,  2 ],
              [ 2 ,  0 ,  0 ],
              [ 0 ,  1 , - 1 ]])
scaler =  preprocessing.StandardScaler().fit(X)
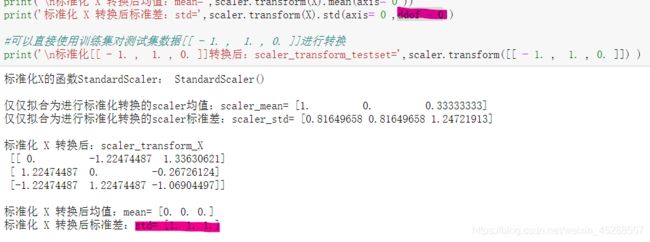
print('标准化X的函数StandardScaler：',scaler)

 
print('\n仅仅拟合为进行标准化转换的scaler均值：scaler_mean=',scaler.mean_)
print('仅仅拟合为进行标准化转换的scaler标准差：scaler_std=',np.sqrt(scaler.var_)) #var_算的是训练集的方差
 
print('\n标准化 X 转换后：scaler_transform_X\n',scaler.transform(X) )
print('\n标准化 X 转换后均值：mean=',scaler.transform(X).mean(axis= 0 ))
print('标准化 X 转换后标准差：std=',scaler.transform(X).std(axis= 0 ))

#可以直接使用训练集对测试集数据[[ - 1. ,  1. , 0. ]]进行转换
print('\n标准化[[ - 1. ,  1. , 0. ]]转换后：scaler_transform_testset=',scaler.transform([[ - 1. ,  1. , 0. ]]) )

训练好模型后进行预测时，新的输入数据要按照训练数据集的均值和标准差进行标准化，然后代入到模型生成预测值

补充Python计算标准差“std”的知识点：

在统计学中，多年的经验总结出：

• 如是总体,标准差公式根号内除以 n
• 如是样本,标准差公式根号内除以（n-1）
• 计算得出的默认标准偏差类型在 numpy.std() 和 pandas.std() 函数之间是不同的。
  • 默认情况下，numpy 计算的是总体标准偏差，ddof = 0；
  • pandas 计算的是样本标准偏差，ddof = 1。如果我们知道所有的分数，那么我们就有了总体——因此，要使用 pandas 进行归一化处理，我们需要将“ddof”设置为 0。
  • 在标准化时用的总体标准差 ddof = 0。scale官网的Notes中
    表示选择ddof不太可能影响模型性能。下面是小编用上面的例子继续进行的测试：
    所以可以看出用的是总体标准差。

2、区间缩放——将特征缩放至特定范围内

一种标准化是将特征缩放到给定的最小值和最大值之间，通常在 0 和 1 之间，但也有归一到 [ -1，1 ] 的情况，可以分别使用 MinMaxScaler 和 MaxAbsScaler 实现。这些归一化不是整个矩阵归一化！是 一列一列进行的归一化！！！

使用这种缩放的目的包括实现特征极小方差的鲁棒性以及在稀疏矩阵中保留零元素。

2.1、MinMaxScaler：缩放到 [ 0，1 ]

如果给 MinMaxScaler 提供一个明确的 feature_range=(min, max) ，完整的公式是:
$$X_s\text{ caled }=\frac{(X-X.min(axis=0))}{(X.max(axis=0)-X.min(axis=0))}\cdot (\max -\min )+\min$$

X.max (axis=0)和X.min(axis=0)是指每列的最大、最小值，min, max默认为 default=(0, 1)

#即默认状态为：
X_std = (X - X.min(axis=0)) / (X.max(axis=0) - X.min(axis=0))
X_scaled = X_std * (1 - 0) + 0

从原理中我们注意到有一个axis=0，这表示MinMaxScaler方法默认是对每一列做这样的归一化操作，这也比较符合实际应用。

例子：将数据归一到 [ 0，1 ]

from sklearn import preprocessing
import numpy as np
 
x = np.array([[3., -1., 2., 613.],
              [2., 0., 0., 232],
              [0., 1., -1., 113],
              [1., 2., -3., 489]])
 
min_max_scaler = preprocessing.MinMaxScaler()
x_minmax = min_max_scaler.fit_transform(x)
print(x_minmax)

如果有新的测试数据进来，也想做同样的转换，那么将新的测试数据添加到原数据末尾即可

from sklearn import preprocessing
import pandas as pd
 
min_max_scaler = preprocessing.MinMaxScaler()
 
x = ([[3., -1., 2., 613.],
      [2., 0., 0., 232],
      [0., 1., -1., 113],
      [1., 2., -3., 489]])#原数据
 
y = [7., 1., -4., 987]#新的测试数据
x.append(y)#将y添加到x的末尾

print('添加新数据后的x ：\n', x)
x_minmax = min_max_scaler.fit_transform(x)
print('\n归一化后的x_minmax :\n', x_minmax)

结果：每一列特征中的最小值min变成了0，最大值max变成了 1。

2.2、MaxAbsScaler：缩放到 [ -1，1 ]

它只通过除以每个特征的最大值将训练数据特征缩放至 [-1, 1] 范围内，以使训练集中每个特征的最大绝对值为1.0，这就意味着，训练数据应该是已经零中心化或者是稀疏数据。

from sklearn import preprocessing
import numpy as np
 
x = np.array([[3., -1., 2., 613.],
              [2., 0., 0., 232],
              [0., 1., -1., 113],
              [1., 2., -3., 489]])
max_abs_scaler = preprocessing.MaxAbsScaler()
x_train_maxsbs = max_abs_scaler.fit_transform(x)
print(x_train_maxsbs)

如果有新的测试数据进来，和原来的表一起进行归一化：

from sklearn import preprocessing
import pandas as pd
 
max_abs_scaler = preprocessing.MaxAbsScaler()
 
x = ([[3., -1., 2., 613.],
              [2., 0., 0., 232],
              [0., 1., -1., 113],
              [1., 2., -3., 489]])#原数据
 
y = [5., 1., -4., 888]#新的测试数据
x.append(y)
print('x ：\n', x)
x_train_maxsbs = max_abs_scaler.fit_transform(x)
print('x_train_maxsbs :\n', x_train_maxsbs)

3、缩放有离群值的数据

如果你的数据包含许多异常值，使用均值和方差缩放可能并不是一个很好的选择。这种情况下，你可以使用 robust_scale 以及 RobustScaler 作为替代品。它们对你的数据的中心和范围使用更有鲁棒性的估计。

4、核矩阵的中心化

• 核函数：在低维输入空间中通过某个函数就能得到等同于将输入空间映射到高维特征空间进行内积计算后的值，这个函数就称为核函数
• 核矩阵：将N个样本，每两个样本进行一次核函数影射得到的N*N维的矩阵，称为核矩阵

设K(x，z)是由phi(x)^ T phi(z)定义的核矩阵，其中phi是将x映射到希尔伯特空间的函数。

KernelCenterer 类构造过程中不需要设定任何参数，只在 fit 过程中需要传入核矩阵，之后进行转换。实质上，KernelCenterer 中心化数据的过程就是将数据集转换为零均值的归一化过程。但却不明确地计算phi(x)。可以认为它是使用sklearn.preprocessing.StandardScaler(with_std=False) 将 phi(x) 居中。

5、非线性转换

有两种类型的转换是可用的:分位数转换和幂函数转换。这两种变换都是单调变换，这样，保证了变换前后的秩关系是一致的（即保持每个特征的值的排序关系）。

分位数变换：假设特征 $X$ ，$F(X)$ 是特征的累积分布函数，所有特征的共同输出分布 $G$。$G^{-1}$是 $G$ 的分位数函数，根据公式$G^{-1}(F(X))$，分位数变换将所有特征变换到相同的分布。这个公式基于以下两个事实：

1. 如果 $X$ 是具有连续累积分布函数 $F$ 的随机变量，那么$F(X)$是[0,1]上的均匀分布；
2. 如果 $U$ 是[0,1]上的均匀分布，那么$G^{-1}(U)$有分布 $G$。

通过执行秩变换，分位数变换平滑了异常分布，并且比缩放方法受异常值的影响更小。但是它的确使特征间及特征内的关联和距离失真了。
目的：将所有特征置于相同的期望分布中

幂变换则是一组参数变换，其目的是将数据从任意分布映射到接近高斯(正态)分布的位置。

• PowerTransformer目前提供了两个这样的幂变换，Yeo-Johnson变换和Box-Cox变换，利用极大似然估计了稳定方差和最小偏度的最优参数。并且，Box-Cox要求输入数据严格为正数据，而Yeo-Johnson支持正负数据。

5.1、映射到均匀分布

QuantileTransformer 类以及 quantile_transform 函数提供了一个基于分位数函数的无参数转换，将数据映射到了0到1的均匀分布上:

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn import preprocessing
import numpy as np
import matplotlib.pyplot as plt

#加载iris dataset
iris = load_iris()
#提取特征X和目标值y：extrant the features and the target
X, y = iris.data, iris.target
#区分训练集和测试集split the dataset into training dataset and testing dataset
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state = 0)
#Quantile_transformer的构造：construction of quantile_transformer
quantile_transformer = preprocessing.QuantileTransformer(random_state = 0)
#transform the train data by quantile_transformer
X_test_trans = quantile_transformer.fit_transform(X_test)
#print the qth percentitles of the array elements
#print(X_test)
#print(X_test_trans)
#print()
#np.percentile(X_train[:, 0], [0, 25, 50, 75, 100]) #计算一个多维数组的任意百分比分位数，此处的百分位是从小到大排列
#np.percentile(X_test[:, 0], [0, 25, 50, 75, 100])
#np.percentile(X_test_trans[:, 0], [0, 25, 50, 75, 100])

plt.scatter(X_test[:, 0], X_test_trans[:, 0])

关于np.percentile()参考：https://blog.csdn.net/weixin_40845358/article/details/84638449

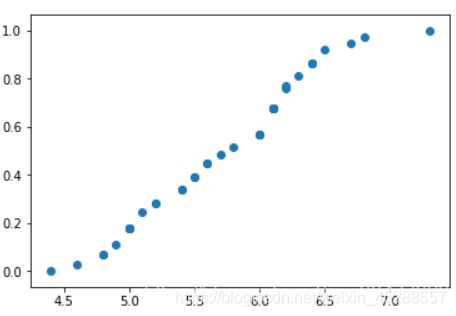
从这个图中我们可以十分清楚的看到实际上，这个映射是将原始的数据集按照累积概率密度函数 $F(X)$ 来进行映射的，将每个离散值映射到其累积概率分布，映射之后的 $X$ 是均匀分布。原理如下，根据：
$$F(X)=X——（1）$$
$$F(X)={\int }_0^{X}p(t)\mathrm{d}t——（2）$$
同时对两式的 $X$ 求导可得：
$$p(X)=1$$

故，随机变量 $X$ 是服从均匀分布的，且范围为0~1

5.2、映射到高斯分布

在生活中有很多数据都是类似的符合正态分布，比如一个统计量：每个人的年度消费。按照道理我们想呀，这个应该是符合正态分布的，我们就拿到了数据，正在规划基于满足正态分布的消费数据做一些分类决策树，或者其它的小东西。但是！我们为了课题的严谨性，要检验一下找个数据到底是不是正态分布，结果喜闻乐见，它不满足正态分布。（当然此刻我们可以假装它满足，从认真建模，到瞎编数据系列）我们要对它进行正态分布变换，这个有很多方法，取对数、开方。

这里介绍一种BOX—COX变换，也就是经常做数据科学口中的BC变换，这个是一个很好对数据进行正态分布变换的一种方法。有一种scipy库的方法：使用scipy.stats.boxcox完成BoxCox变换，可自行参考。

Box-Cox变换，用来降低 特征X 的偏度值,达到接近正态分布的目的

在许多建模场景中，需要数据集中的特征的正态化。幂变换是一类参数化的单调变换， 其目的是将数据从任何分布映射到尽可能接近高斯分布，以便稳定方差和最小化偏斜。

类 PowerTransformer 目前提供两个这样的幂变换,Yeo-Johnson transform 和 the Box-Cox transform。在这两种方法中，变换都是参数化的，通过极大似然估计来确定。

Box-Cox要求输入数据严格为正数据，而Yeo-Johnson支持正负数据。

• Yeo-Johnson transform:
  $$x_i^{(\lambda )}=\{\begin{array}{ll}\left[{\left(x_i+1\right)}^{\lambda }-1\right]/\lambda & \text{ if }\lambda \ne 0,x_i\ge 0\\ \ln \left(x_i\right)+1& \text{ if }\lambda =0,x_i\ge 0\\ -\left[{\left(-x_i+1\right)}^{2-\lambda }-1\right]/(2-\lambda )& \text{ if }\lambda \ne 2,x_i<0\\ -\ln \left(-x_i+1\right)& \text{ if }\lambda =2,x_i<0\end{array}$$
  Johnson转换与Box-Cox转换相比的优越性
• Box-Cox transform:
  $$x_i^{(\lambda )}=\{\begin{array}{ll}\frac{x_i^{\lambda }-1}{\lambda }& \text{ if }\lambda \ne 0\\ \ln \left(x_i\right)& \text{ if }\lambda =0\end{array}$$

5.2.1、下面是一个使用Box-Cox将样本从对数正态分布映射到正态分布的例子:

import numpy as np
from sklearn.preprocessing import PowerTransformer
pt=PowerTransformer(method='box-cox',standardize=False)
#生成对数正态分布的随机数
X_lognormal=np.random.RandomState(616).lognormal(size=(3,3))
print('展示符合正态分布的随机数：\n',X_lognormal)

继续输入：

pt.fit_transform(X_lognormal)

上述例子设置了参数standardize的选项为 False 。 但是，默认情况下为“True”，类PowerTransformer会将输出值转换为符合标准正态的值：零均值zero-mean、单位方差归一化unit-variance normalization。

5.2.2、使用PowerTransformer类默认的default=’yeo-johnson’：

#import numpy as np
from sklearn.preprocessing import PowerTransformer
pt = PowerTransformer()
data = [[1, 2], [3, 2], [4, 5]]
print(pt.fit(data))
print('\n参数λ=',pt.lambdas_)
print('\n拟合后的数据\n',pt.transform(data)) #Fit to data, then transform it.

5.2.3、 两种方法的对比结果：

5.2.4、强调了在幂变换前后对数据进行 可视化 的重要性

发现有时候幂变换不一定有效。应用到某些分布上的时候， 幂变换得到的分布非常像高斯分布，但是对另一些分布，结果却不太有效。

我们也可以 使用类 QuantileTransformer (通过设置 output_distribution='normal')把数据变换成一个正态分布。下面是将其应用到 iris dataset 上的结果:

from sklearn.datasets import load_iris
iris = load_iris()
X    = iris.data
from sklearn import preprocessing
quantile_transformer = preprocessing.QuantileTransformer(output_distribution='normal', random_state=0)
X_trans = quantile_transformer.fit_transform(X)
quantile_transformer.quantiles_

输出：

array([[4.3, 2. , 1. , 0.1],
       [4.4, 2.2, 1.1, 0.1],
       [4.4, 2.2, 1.2, 0.1],
       ...,
       [7.7, 4.1, 6.7, 2.5],
       [7.7, 4.2, 6.7, 2.5],
       [7.9, 4.4, 6.9, 2.5]])

因此，输入数据的中值变成了输出数据的均值，以0为中心。正态输出被裁剪，以便输入的最大最小值(分别对应于1e-7和-1e-7)不会在变换之下变成无穷。

6、归一化

简单来说，标准化是依照特征矩阵的列处理数据，其通过求z-score的方法，将样本的特征值转换到同一量纲下。归一化是依照特征矩阵的行处理数据，其目的在于样本向量在点乘运算或其他核函数计算相似性时，拥有统一的标准，也就是说都转化为“单位向量”。归一化类型包括：线性归一化、标准差归一化和非线性归一化。规则为 $l2$ 的归一化公式如下：
$$x^{\prime }-\frac{x}{\sqrt{{\sum }_j^{m}x[j{]}^2}}$$

这个观点基于 向量空间模型(Vector Space Model) ，经常在文本分类和内容聚类中使用.

函数 normalize 提供了一个快速简单的方法在类似数组的数据集上执行操作，使用 l1 或 l2 范式:

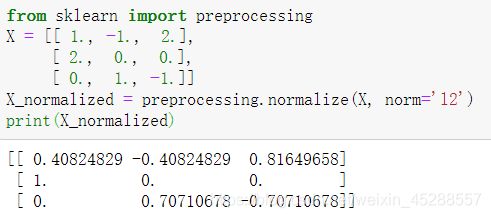
from sklearn import preprocessing
X = [[ 1., -1.,  2.],
     [ 2.,  0.,  0.],
     [ 0.,  1., -1.]]
X_normalized = preprocessing.normalize(X, norm='l2')
print(X_normalized)

7、类别特征编码

在机器学习中，特征经常不是连续的数值型的而是标称型的(categorical)。

举个例子，一个人的样本具有特征

• [“male”, “female”],
• [“from Europe”, “from US”, “from Asia”],
• [“uses Firefox”, “uses Chrome”, “uses Safari”, “uses Internet Explorer”]
• 等

这些特征能够被有效地编码成整数，比如 :

• [“male”, “from US”, “uses Internet Explorer”] 可以被表示为 [0, 1, 3]
• [“female”, “from Asia”, “uses Chrome”] 表示为 [1, 2, 1]

要把标称型特征(categorical features) 转换为这样的整数编码(integer codes), 我们可以使用 OrdinalEncoder 。 这个估计器把每一个categorical feature变换成 一个新的整数数字特征 (0 到 n_categories - 1):

from sklearn import preprocessing
enc = preprocessing.OrdinalEncoder()
X = [['male', 'from US', 'uses Safari'], ['female', 'from Europe', 'uses Firefox']]
enc.fit(X) 

enc.transform([['female', 'from US', 'uses Safari']])

这样的整数特征表示并不能在scikit-learn的估计器中直接使用，因为这样的连续输入，估计器会认为类别之间是有序的，但实际却是无序的。(例如：浏览器的类别数据是任意排序的)。

另外一种将标称型特征转换为能够被scikit-learn中模型使用的编码是one-of-K， 又称为 独热码或dummy encoding。 这种编码类型已经在类OneHotEncoder中（注意名称和上面的 OrdinalEncoder 不是同一个名字）实现。该类把每一个具有n_categories个可能取值的categorical特征变换为长度为n_categories的二进制特征向量，里面只有一个地方是1，其余位置都是0。

继续上面的例子:

from sklearn import preprocessing
enc = preprocessing.OneHotEncoder()
X = [['male', 'from US', 'uses Safari'], ['female', 'from Europe', 'uses Firefox']]
enc.fit(X)  

enc.transform([['female', 'from US', 'uses Safari'],
               ['male', 'from Europe', 'uses Safari']]).toarray()

默认情况下，每个特征使用几维的数值可以从数据集自动推断。而且也可以在属性categories_中找到:

enc.categories_

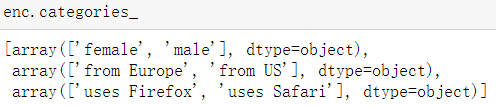
可以使用参数categories_显式地指定这一点。我们的数据集中有两种性别、四种可能的大陆和四种web浏览器:

from sklearn import preprocessing
genders = ['female', 'male']
locations = ['from Africa', 'from Asia', 'from Europe', 'from US']
browsers = ['uses Chrome', 'uses Firefox', 'uses IE', 'uses Safari']
enc = preprocessing.OneHotEncoder(categories=[genders, locations, browsers])
# Note that for there are missing categorical values for the 2nd and 3rd
# feature
X = [['male', 'from US', 'uses Safari'], ['female', 'from Europe', 'uses Firefox']]
enc.fit(X)

enc.transform([['female', 'from Asia', 'uses Chrome']]).toarray()

如果训练数据可能缺少分类特性，通常最好指定handle_unknown='ignore'，而不是像上面那样手动设置类别。当指定handle_unknown='ignore'，并且在转换过程中遇到未知类别时，不会产生错误，但是为该特性生成的一热编码列将全部为零(handle_unknown='ignore'只支持一热编码):

如果训练数据中可能含有缺失的标称型特征, 通过指定handle_unknown='ignore'比像上面代码那样手动设置categories更好。 当handle_unknown='ignore' 被指定并在变换过程中真的碰到了未知的 categories, 则不会抛出任何错误,但是由此产生的该特征的one-hot编码列将会全部变成 0 。(这个参数设置选项 handle_unknown='ignore' 仅仅在 one-hot encoding的时候有效):
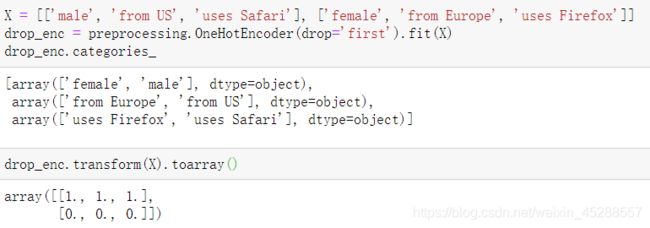
还可以使用drop参数将每个列编码为n_categories-1列，而不是n_categories列。此参数允许用户为要删除的每个特征指定类别。这对于避免某些分类器中输入矩阵的共线性是有用的。

例如，当使用非正则化回归(线性回归)时，这种功能是有用的，因为共线性会导致协方差矩阵是不可逆的。当这个参数不是None时，handle_unknown必须设置为error:
标称型特征有时是用字典来表示的，而不是标量，具体请参阅从字典中加载特征。

8、离散化

离散化 (Discretization) (有些时候叫 量化(quantization) 或 装箱(binning)) 提供了将连续特征划分为离散特征值的方法。 某些具有连续特征的数据集会受益于离散化，因为 离散化可以把具有连续属性的数据集变换成只有**名义属性(nominal attributes)**的数据集。 (译者注： nominal attributes 其实就是 categorical features, 可以译为 名称属性，名义属性，符号属性，离散属性 等)

One-hot 编码的离散化特征 可以使得一个模型更加的有表现力(expressive)，同时还能保留其可解释性(interpretability)。 比如，用离散化器进行预处理可以给线性模型引入非线性。

详情可参考http://scikitlearn.com.cn/0.21.3/40/

9、缺失值补全

详情可参考http://scikitlearn.com.cn/0.21.3/41/

10、自定义转换器

在机器学习中，想要将一个已有的 Python 函数转化为一个转换器来协助数据清理或处理。可以使用 FunctionTransformer 从任意函数中实现一个转换器。

感觉这是高端玩家的选择，哈哈~

详情可参考http://scikitlearn.com.cn/0.21.3/40/

参考：

• http://scikitlearn.com.cn/0.21.3/40/
• https://blog.csdn.net/weixin_40683253/article/details/81508321
• https://www.cnblogs.com/geo-will/p/9626196.html