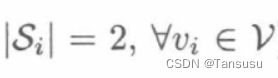复杂网络上的博弈及其演化动力学读书笔记

读书笔记DAY 1 - 复杂网络上的博弈及其演化动力学

---

我是一个时间戳
2021/4/30 14:55:46 
这是我开始的日子嘻嘻

Hello,朋友们又见面啦，自从这个月13号接到导师的任务，我也不知道怎么解释前面的大半个月自己在干嘛，自欺欺人的说是在做前期准备吧，现在决定正式开始努力啦，在啃书啃论文的同时也会加入自己的理解，偶尔努力但是经常碎碎念，大家一起加油哇（手动可爱:D

---

复杂网络

• 复杂网络由节点以及节点之间的连线构成，节点-系统的基本组成单元，连线-系统中个单元之间的交互关系

演化博弈

• 演化博弈是刻画群体决策形成和演化的一种基本范式，结合了传统博弈论与生物进化论。以参与群体为研究对象，通过分析群体策略在选择和突变作用下的演化过程，从而解释和预测个体在交互决策情境中的博弈行为。（从系统动态的角度考察个体决策到群体决策的形成机制）

复杂网络上的演化博弈

• 复杂网络上的演化博弈是一种自下而上的科学范式，从个体的行为规则、个体之间的交互方式和结构进行建模，来探讨群体行为的形成和演化机制。
• NOTE：将系统行为作为一个整体的研究方式不受传统还原论方法的限制，从而能够预言复杂系统丰富的整体行为。

研究方向

1. 从个体到群体：即通过对个体之间的交互关系网络和决策动力学进行建模和分析，定量研究并预测网络群体的博弈动力学行为。
2. 从群体到个体：即根据对群体策略的要求，设计个体之间的交互机制或对个体的决策动力学进行干预，使得网络群体的整体行为能够达到预期设定的要求。

---

此书可以分为三大部分

• 第一部分
  • 1-2章 博弈论和演化博弈论的基本概念以及相关的动力模型
• 第二部分
  • 3-6章 复杂网络上的博弈及演化动力学模型
    • 1.网络博弈模型的概念
    • 2.复杂网络上的随机漂移过程
    • 3.复杂网络上的常数选择过程
    • 4.复杂网络上的演化博弈过程
• 第三部分
  • 7-10章 复杂网络上的演化博弈热门主题
  1. 复杂网络上的合作涌现机制
  2. 符号网络上的演化博弈
  3. 行为网络上的演化博弈
  4. 博弈学习动力学在分布式协同控制的应用

---

第一章 博弈论简介

• 博弈论是研究多个自主体在利益相关情形下的决策行为的理论。
• 多个个体具有独立决策的自主性，它们的利益却相互关联或冲突，博弈论通过建立适当的数学模型和工具，来分析、预测和干预自主个体在利益相关情形下的决策行为。

1.1 什么是博弈

• 博弈的三要素：决策个体集合V（player set） 每个决策者所能采用的策略集合S（strategry set） 每个决策者的收益函数U（payoff function）

• 两人博弈：n=2

• 多人博弈：n>2

• 有限策略博弈：每个个体策略集具有有限个元素

• 两策略博弈：
  

  Q：为什么要加绝对值？
  G：策略集合还可能为负？或者是说策略集合理元素的方向完全相反表示负？

• 连续策略博弈：某个个体的策略集为连续集合

• 对称博弈：个体收益与个体本身无关，仅却决于与它交互的其它策略。
  

1.囚徒困境博弈（prisoner’s dilemma game） -合作困境

两个囚徒，每个人都有合作和背叛两种选择，都选择合作，每人收益R；都选择背叛，每人收益P；一个选择合作一个选择背叛，合作者收益S，背叛者收益T，收益矩阵如下：

NOTE:收益函数满足T>R>P>S

PS:合作困境：每个个体都倾向于采取有利于自身的策略，最终会导致一个不利于任何个体的结果。

2.公共物品博弈(public goods game) -合作困境

典型多人两策略博弈，，每个个体需要决定是否往公共资金里投入一定的资金c>0(合作策略)或者不如此（背叛策略）。这笔公共资金乘以r>1后，另A和B分别表示合作策略和背叛策略，可以有：

PS:合作困境：不管其它个体采取什么策略，背叛策略总能带给个体更多的收益，当所有个体都采取背叛策略时收益为0，小于所有个体都采取合作策略时的收益(r-1)c

3.志愿者困境博弈(volunteer’s dilemma game)

另一类典型多人两策略博弈，有一个问题需要解决，如果团体中有任何一个人付出一定代价c>0（合作行为），问题就可以被解决，其他成员不用付出任何代价；但如果所有人都等待其他人付出（背叛行为），则问题会一直持续到有人解决，问题的持续会给每个人造成a>c>0的代价。

合作困境：每个个体都存在等待他人来解决问题的倾向。

上述收益矩阵和收益表格通常用来刻画有限策略博弈，对于连续策略博弈通过收益函数来刻画。

4.多个体一致性博弈(volunteer’s dilemma game)

一个有多个可在二维平面内移动的机器人组成的多个体系统，系统的目的是使多个机器人达到同一位置，可以通过多个体一致连续性质博弈来刻画。（欧氏距离定义）

续：每个个体按照梯度动力学更新自己的策略，就可以得到最终所有的个体的策略收敛于一致性状态，即纳什均衡点。（典型一致性协议）

NOTE：当所有个体采取相同的策略（即相同的位置）时，每个个体才能获得最大的收益。

纯策略和混合策略

1. 纯策略 pure strategy：个体只能从其策略集合重选择一种特定策略的方式。
2. 混合策略 mixed strategy：个体给其策略集合中的每个策略赋予一定的概率，同时按照概率分布随机选择一种策略。(如果个体的策略集合是连续的，混合策略可以通过一个连续概率分布来表示)

博弈的混合扩展->派生

1.2博弈解的概念

理性 (rational)是博弈论中对决策者的一个经典假设，理性假设要求个体具备完备的计算和推理能力，能够计算每种策略给自己所带来的收益，并且以实现收益最大化为目标。通常假设“每个决策者都是理性的”是公共知识（common knowledge），公共知识要求：每个个体都是理性的，每个个体都知道其他所有个体是理性的…

1. 占优策略均衡

在一些博弈中，不论其他个体采取什么策略，某一策略总是比另一策略给个体带来更多的收益，带来更多收益的策略为占优策略(dominant strategy)，另一个策略为劣势策略(dominanted strategy)

占优策略：（严格）占优策略（strictly dominant strategy）带给个体更多的收益，理性个体优先选择。

占优策略均衡：（严格）占优策略均衡点，每个个体的策略都是一个（严格）占优策略。
如果一个博弈存在（严格）占优策略均衡，则可以预测每个理性个体都将采取占优策略均衡所对应的策略。

劣势策略：（严格）劣势策略（strictly dominanted strategy）是理性个体应该避免的策略。

2. 纳什均衡 Nash equilibrium

占优策略均衡来预测和分析参与个体在博弈中的决策行为存在很大的局限性，因此有了纳什均衡。

NOTE：

• 占优策略均衡：一个策略（针对一个个体）
• 纳什均衡：一个策略组合（针对多个个体）

1. 纯策略纳什均衡

当所有个体采用策略组合时，没有任何一个个体可以通过单方面改变自身的策略来获取更高的收益。因此，纳什均衡可以看作一个稳定的策略组合。

对于由一个博弈延伸出的混合扩展博弈，可以定义混合策略纳什均衡。

2. 混合策略纳什均衡

严格混合策略纳什均衡，纳什均衡可以通过最优响应策略(best-response strategy)的形式定义，一个个体的最优响应策略是指使这个个体收益最大化的策略集合。

3. 最优响应策略

每个个体的最优响应策略是一个集值映射，在纳什均衡中，每个个体的策略是关于其他个体策略组合的最优响应策略，则纳什均衡是最优响应函数的不动点。

定理一：纳什均衡的存在性证明。
定理二：任何有限策略博弈都具有至少一个混合策略纳什均衡点。（针对混合策略，纯策略纳什均衡不一定存在）。
定理三：对于一个博弈，如果每个个体的策略集合是欧氏空间中的一个非空闭凸集，且每个个体的收益函数是关于每个个体策略集合的连续拟凹函数，那么这个博弈具有一个纯策略纳什均衡点。

4. 势博弈

势博弈(potential game)，一定存在至少一个纯策略纳什均衡点，且其纳什均衡点对应势博弈函数的最大值点。
（定理四：关于势博弈上的一个纯纳什均衡点）

1.3 博弈学习动力学简介

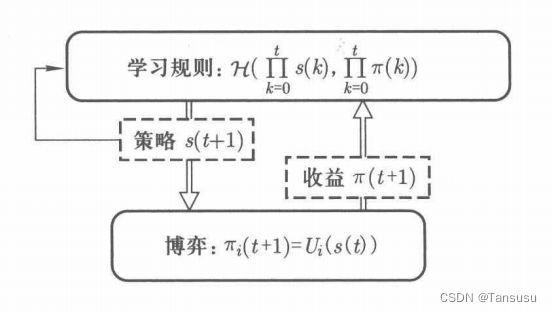
博弈学习：参与个体如何根据所获得的关于博弈以及其他个体策略和收益等信息，不断地调整自己的策略，最终达到纳什均衡点。

1. 博弈学习框架
   在博弈学习框架中，同一个博弈被假定重复多次，称为重复博弈。

博弈学习框架示意图：

收益信息可以间接地由个体策略和收益函数得到，每个个体的学习规则Hi可以是确定性函数或随机函数，利用上述所有信息来确定下一步的策略。

每个个体的更新策略的时序，可以将博弈学习分为同步学习、异步学习、顺序学习和随时时序学习：

1. 同步学习(synchronous learning)：在每个时刻t所有个体依据对应的学习规则，同时更新自身的策略。

2. 异步学习(asynchronous learning)：在每个时刻t只有一部分个体更新自己的策略，其他个体保持其原来的策略不变。

3. 顺序学习(sequential learning)：个体依照指定的次序依次更新自己的策略，每个时刻t，只有一个个体更新自身的策略，其他个体保持原来的策略不变。

4. 随机时序学习(random-timing learning)：每个时刻t，按照一定的概率选择一个个体更新自己的策略。

5. 最优响应动力学 best-response dynamics

个体在假定其他个体策略保持不变的情况下，从其最优响应策略中任意选择一个策略，作为下一步的策略。

局限性：

1. 个体需要获取其他所有个体的策略信息，以及其自身收益函数的解析形式，限制了最优响应动力学的实际应用。

2. 最优响应动力学需要求解最优响应策略这一优化问题，可能需要很大的计算量甚至不可能实现。

3. 按照最优响应动力学，个体每一步的策略可能发生很大的改变，但是在实际中，可能策略只能在一个很小的范围内渐变。

4. 择优响应动力学 better-response dynamics
   即每个个体选择使自己收益有所提升的策略，计算量更小。

在每个时间步，个体在假定其他个体策略保持不变的情况下，从其择优响应策略中任意选择一个策略，作为下一步时间步的策略。（最常见的梯度动力学）

第一章到此就结束啦

总结

第一章主要学习了标准形式的博弈模型、博弈的解以及博弈学习动力学，即为应用博弈理论解决实际问题的三个步骤：

1. 博弈模型：用于对利益相关情形下的各类实际系统进行建模
2. 博弈的解（主要是纳什均衡）：对应实际系统的设计目标
3. 博弈学习动力学：用于设计实际系统的协同控制算法，以实现设计目标

 我是一个时间戳
 2021/5/15 0:10:07 
 啊 第一章终于结束啦