sklearn.metrics 用法详解

1. 用法概览

1.1 分类

函数	功能
metrics.accuracy_score	准确率
metrics.balanced_accuracy_score	在类别不均衡的数据集中，计算加权准确率
metrics.top_k_accuracy_score	获得可能性最高的k个类别
metrics.average_precision_score	根据预测分数计算平均精度 (AP)
metrics.brier_score_loss	Brier 分数损失
metrics.f1_score	F1 score
metrics.log_loss	交叉熵损失
metrics.precision_score	精确率
metrics.recall_score	召回率
metrics.jaccard_score	Jaccard 相似系数得分
metrics.roc_auc_score	根据预测分数计算 Area Under the Receiver Operating Characteristic Curve(ROC AUC) 下的面积
metrics.cohen_kappa_score	衡量注释间一致性的统计量

1.2 聚类

函数	功能
metrics.adjusted_mutual_info_score	两个聚类之间的调整互信息(AMI)
metrics.adjusted_rand_score	调整兰德指数
metrics.completeness_score	给定GT的集群标记的完整性度量
metrics.fowlkes_mallows_score	测量一组点的两个聚类的相似性
metrics.homogeneity_score	同质性指标
metrics.mutual_info_score	互信息
metrics.normalized_mutual_info_score	标准化互信息
metrics.rand_score	兰德指数
metrics.v_measure_score	V测度得分

1.3 回归

函数	功能
metrics.explained_variance_score	解释方差回归评分函数
metrics.mean_absolute_error	平均绝对误差
metrics.mean_squared_error	均方误差
metrics.mean_squared_log_error	平均平方对数误差
metrics.median_absolute_error	中位数绝对误差
metrics.r2_score	$R^2$(确定系数)

2. 数学原理

主要记录一下关于分类部分的数学原理。准确率 - accuracy，精确率 - precision，召回率 - recall，
F1值 - F1-score，ROC曲线下面积 - ROC-AUC （area under curve），PR曲线下面积 - PR-AUC。

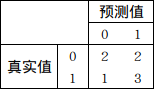
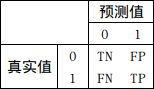
对于一个二分类问题，假设真实标签y_labels=[1,1,0,1,1,0,0,0]，我们预测的结果y_scores=[0.8,0.9,0.6,0.3,0.7,0.1,0.1,0.6]。假设threshold=0.5。那么可以得到y_preds=[1,1,1,0,1,0,0,1]。这时我们可以得到混淆矩阵(confusion matrix)为：

图1：混淆矩阵

混淆矩阵中所对应的每一个值的含义如下：

图2：混淆矩阵的含义

那么：
准确率=$\frac{TP+TN}{TP+TN+FP+FN}$，精准率=$\frac{TP}{TP+FP}$，召回率=$\frac{TP}{TP+FN}$，F1-scores=$\frac{2\ast Precision\ast Recall}{Precision+Recall}$。

ROC/AUC的概念

ROC（Receiver Operating Characteristic）曲线，又称接受者操作特征曲线。该曲线最早应用于雷达信号检测领域，用于区分信号与噪声。后来人们将其用于评价模型的预测能力，ROC曲线是基于混淆矩阵得出的。

灵敏度（Sensitivity）= $\frac{TP}{TP+FN}$，特异度（Specificity）=$\frac{TN}{FP+TN}$
真正率（TPR）= 灵敏度= $\frac{TP}{TP+FN}$，假正率（FPR） = 1- 特异度 =$\frac{FP}{FP+TN}$

在上述二分类的例子中，我们取threshold=0.5可以的到一个y_preds，threshold从0取到1就可以得到不同的y_preds，进而计算出不同的（FPR，TPR）对。它们在坐标轴上对应了一条曲线，这条曲线就是ROC曲线，曲线下的面积就是AUC的值。如下图：

图3：ROC 曲线

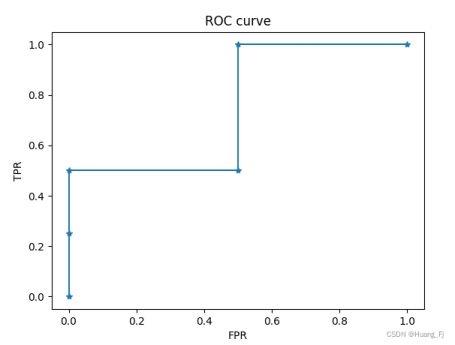
多分类的计算
metrics.cohen_kappa_score：继续等待填坑

3. 实例

以之前的数据来计算每一个度量指标的值，这里用metrics.classification_report。
metrics.classification_report(y_true, y_pred, *, labels=None, target_names=None, sample_weight=None, digits=2, output_dict=False, zero_division='warn')
注意到这里的参数是y_pred而不是y_score，所以它只能计算F1-score，而不能计算AUC值。
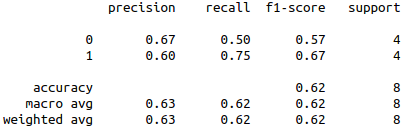
返回值的格式如下：
{'label 1': {'precision':0.5, 'recall':1.0, 'f1-score':0.67, 'support':1}, 'label 2': { ... }, ... }

from sklearn import metrics
import matplotlib.pyplot as plt

y_labels = [1,1,0,1,1,0,0,0]
y_scores=[0.8,0.9,0.6,0.3,0.2,0.1,0.1,0.6]
y_preds = [1,1,1,0,1,0,0,1] # threshold=0.5
report = metrics.classification_report(y_labels,y_preds)
fpr, tpr, thresholds = metrics.roc_curve(y_labels,y_scores)
auc = metrics.auc(fpr,tpr)
plt.plot(fpr,tpr,'*-')
plt.ylabel('TPR')
plt.xlabel('FPR')
plt.title('ROC curve')
print(report)

得到ROC曲线如图3所示，report的值如下：

图4：report结果

参考链接：
[1] https://scikit-learn.org/stable/modules/model_evaluation.html
[2] https://blog.csdn.net/qq_27575895/article/details/83781069
[3] https://laurenoakdenrayner.com/2018/01/07/the-philosophical-argument-for-using-roc-curves/