读论文（8）——FCOS

前言

我们在上一篇论文中已经介绍了一种anchor-free（即抛弃掉anchor进行目标检测）的思路，也就是通过检测关键点来定位目标，用关键点去描述目标。这种思路我们一般称之为基于keypoint的anchor-free方法，除了我们上次介绍的CenterNet（检测边界框的中心点） 以外还有 CornerNet（检测边界框的左上角和右下角的关键点）、ExtremeNet（检测边界框的四个角的关键点） 等。这一次我们来介绍另一种思路，称为基于segmentation的anchor-free方法。这种方法和CenterNet的思路有相似之处，不过CenterNet更倾向于预测检测框的中心点，利用offset进一步预测偏移量，并且直接预测宽高两个回归值；而基于segmentation的网络更倾向于找到检测框内任一正样本的像素点，预测该框内点距离框的上下左右四个回归值。本文介绍的的方法名为FCOS，原论文题目为《FCOS: Fully Convolutional One-Stage Object Detection》。

思路简介

我们这里简单来提一下为什么要发展anchor-free方法：
首先，如果我们采用anchor-based方法，那么就意味着我们预先要设置一些超参数，比如anchor的个数、尺寸、长宽比等等，这些超参数对模型性能影响很大；
第二，anchor的尺寸与长宽比是固定的，这意味着其没法对尺度变化大的物体进行很好的检测，而且对于每一个具体任务都要重新设计anchor，泛化能力差；
第三，anchor的数量很多，这样会导致在进行IOU计算等环节时计算和内存的开销都很大；
最后，anchor中绝大多数都是负样本（背景、无目标），这样就会导致正负样本不均衡，影响训练性能。

因此，研究者们一直在想如何把anchor机制抛弃掉，采用其他的方法来解决上述的问题。在这篇文章之前，经典的anchor-free方法主要有CornerNet类方法和DenseBox类方法，前者依靠对关键点的检测来实现目标检测，但是其角点的匹配过程太过复杂，后者又无法解决重叠框预测的问题。这时FCOS应运而生，它把目光投向了一个很经典的目标检测方法——我们在这个系列第一篇就学过的YOLO v1。
其实FCOS和YOLO v1的思路很像。YOLO v1严格来说也是一个抛弃了anchor机制的目标检测方法，它将图片划分成若干grid cell并用每个grid cell预测两个任意形状的目标框再做后处理。不过FCOS比起YOLO v1的分cell预测更加精细，它采用的是逐像素预测的方法，即对每个像素都进行目标检测，判为前景的类回归出框，最后做NMS等后处理。

除了这个逐像素预测的思路之外，FCOS做了两个改进：
（1）用FPN作特征融合和多尺度预测，解决了召回率低和预测框重叠导致的二义性模糊问题；
（2）提出一个centerness（中心度）的概念，来排除预测出来的离中心较远的低质量预测框。

下面具体来看论文针对逐像素预测、多层检测、中心度修正这三个重点做了哪些工作。

逐像素预测

设某层的stride为s，对于特征图$F_i$上的每一个坐标$(x,y)$，将其映射回原图片所在位置为$(\lfloor \frac{s}{2}\rfloor +xs,\lfloor \frac{s}{2}\rfloor +ys)$，加上$\lfloor \frac{s}{2}\rfloor$的原因是为了把每个特征映射回原图感受野的中心。映射成功后，判断该点是否在任何ground truth框内，若在记为正例，与对应的ground truth框进行匹配；否则记为负例，与背景进行匹配。这实际上是将位置直接作为训练样本，在一定程度上也借鉴了anchor的思想，不过用的是不是“锚框”而是“锚点”。
得到点后来回归bounding box，每个框可以记为$B_i=({x_0}^{(i)},{y_0}^{(i)},{x_1}^{(i)},{y_1}^{(i)},c^{(i)})$,前四个值代表左上角和右下角坐标，c代表类别，除了分类的标签，我们也可以得到一个4维的真实的用于回归的偏移向量，计算如下：

四个值的含义如下图所示：

通过体会上述过程，我们可以发现，多数的anchor-based方法只会将和ground truth的IOU足够大的框认为是正样本，而FCOS会得到尽可能多的前景点来训练回归器。这样正负样本数就会更平衡，而这也是FCOS优于很多anchor-based方法的原因。

给定一张输入图像，前向通过整个网络，输出每个像素点的类别得分$p_{x,y}$和回归预测$t_{x,y}$。我们选择类别得分大于0.05的作为正例，根据上面的公式变换获得预测的边界框。

接下来看损失函数。

其中$N_{pos}$为正样本的个数，$L_{cls}$是focal loss的形式，$L_{reg}$是UnitBox的IOU loss。可以看出这也是由预测和回归两部分loss构成的。

多层检测（FPN）

首先我们来看一下普通的CNN直接用于检测会有什么问题：
（1）CNN最终特征图的大的stride会导致相对低的最佳可能召回(best possible recal，BPR)，也就是召回率不高。
（2）重叠框会在训练过程中带来二义性模糊的问题，因为重叠区域的像素需要判断到底该去回归哪个框，如下图所示：

为了解决这两个问题，作者引入了FPN。引入FPN后的网络结构如下图所示：

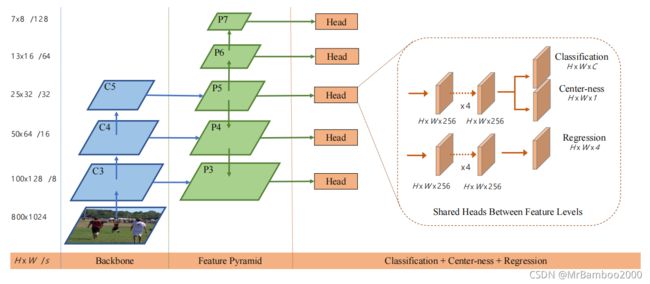
C3、C4、C5层直接做1×1卷积得到P3、P4、P5层，P6、P7层由P5、P6层经过一个stride=2的卷积层得到，这样特征金字塔就构建完成了。

不同于anchor-based检测器在不同特征层上分配不同尺寸的anchor框，作者直接限制边界框的回归范围。满足下列二者之一的都直接被算作负例且不用作边界框的回归：


因为不同尺寸的目标被分配到不同特征层上，而大部分重叠都发生在尺寸差异比较大的目标之间，所以多层级的预测可以缓解上文提到的二义性问题，提高FCN-based检测器的性能，使之接近anchor-based检测器。

此外，作者在不同特征层上加了头部网络，用于分类、计算中心度和回归。这些头部网络共享参数，但是没有完全相同的头部网络作用在不同的特征层上，使用$s_i$可学习的$exp(s_i{x}_i)$来自动调节特征层$P_i$的指数函数。这些操作提升了检测性能。

中心度（centerness）修正

上部分提出的两个问题解决后，作者又发现一个新问题：
通过一个锚点预测会出现大量的远离gt框中心点的低质量预测框。

这又该如何解决呢？

作者在网络中增加了一个和分类分支并列的单层网络分支来预测一个位置的“中心度”（即，该像素位置到该像素对应目标的中心的度量），定义如下：

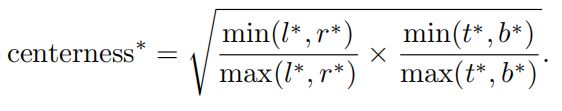
我们可以发现×号前面的部分实际上就是用来衡量是不是在左右的中心，后面的部分用来衡量是不是在上下的中心，开根号则是为了减缓中心度的衰减。中心度的意义和取值如下图所示：

中心度的范围从0到1，因此可以使用二值交叉熵（BCE）损失来训练。这个损失也加到上面“逐像素预测”所示的损失函数上构成新的损失函数。

测试的时候，最终得分为分类的分数和中心度的乘积。因此中心度可以降低远离目标中心边界框的权重，进一步说，这些低质量的边界框大概率会被NMS过滤掉，从而显著提升了检测性能。

做完这一套改进之后，看看和sota方法的对比：

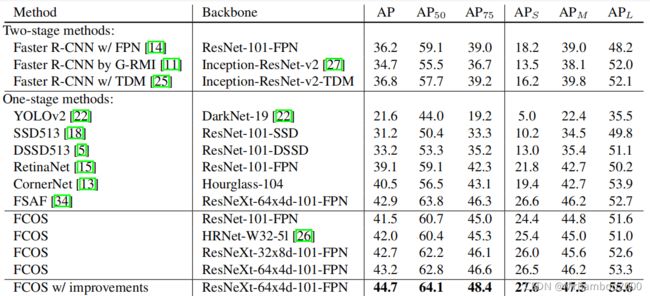
可以发现效果还是很好的。

题外话——anchor-based和anchor-free的本质区别究竟在哪？

上周看了一篇CVPR2020的论文《Bridging the Gap Between Anchor-based and Anchor-free Detection via Adaptive Training Sample Selection》。这篇论文的作者指出，anchor-based和anchor-free的本质区别就在于正负样本的选取方式不同。
作者发现，如果在训练时，RetinaNet和FCOS选择同样的正负样本，最终的表现就不会出现明显的不同，无论是从一个边框来回归，还是一个点来回归。
有了这篇论文的观点与发现，就能很好的解释为什么anchor-free方法有用且效果好：
对于anchor-based方法，太过于依赖anchor的设计，如果anchor不合适，很有可能正样本数量非常少，也就是有很多虽然框到了目标但是没法作为正样本；或者可以理解为对正样本的选择规则设置的不合适。
而anchor-free方法可以很好的找到正样本，先找到中心或者关键点之后再做框，这样能更多更有效地选取正样本。

但是anchor-free方法也不是万能的，往往存在着训练较慢的缺陷，而且有些anchor-free方法的实时性也不是很好。

总结

其实看完这篇论文之后我个人内心是比较感慨的，我的目标检测学习之旅开始于YOLO，现在兜兜转转又回到了YOLO。我们之前学习的很多单阶段检测方法（YOLO v2、v3，SSD），是把anchor机制引入到了类似YOLO v1的框架中，以达到精读的提升；而今天这个方法则是把YOLO v1的思路直接发扬光大，用更密集的检测彻底抛弃掉了需要经过预先设计的anchor。anchor-based也好，anchor-free也好，条条大路通罗马，解决一个问题又很多种思路，而很多情况下，这些思路之间又是相通的。