PyTorch深度学习-02线性模型（快速入门）

---

线性模型

1.步骤

1. 准备数据集DataSet
2. 模型选择Model
3. 训练Training
4. 推理inferring

2.Example

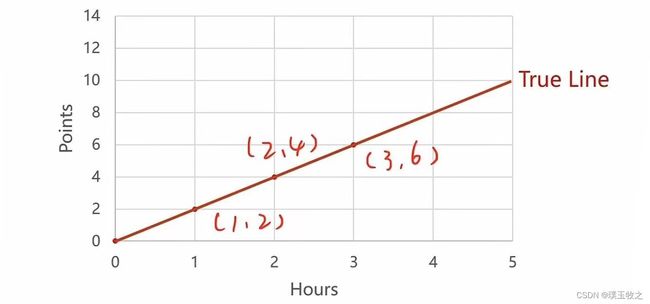
Suppose that students would get y points in final exam,if they spend x hours in paper PyTorch Tutorial.

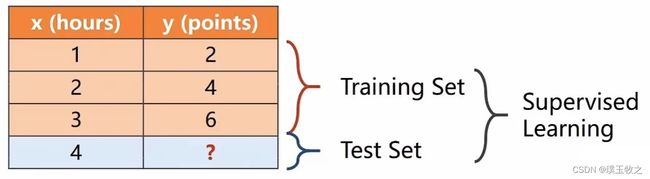
The question is what would be the grade if I study 4 hours?

2.1 Analyse

• 把数据集分为两部分：一部分用于训练，一部分用于测试模型性能

• 会出现的问题： Overfitting(过拟合)：模型过于复杂（所包含的参数过多），以致于模型对训练集的拟合很好，但对未知数据预测很差。

• 解决方法：希望模型有较好的泛化能力，在训练集完成训练后，对于没见过的图像也能够正确识别。

• 通常会把训练集也分成两部分，一部分用于训练，一部分用于进行模型评估（开发集）

2.2 Model design

即找到y=f(x)函数

2.2.1 Linear model (线性模型)

• To simplify the model：
  
• 图像：
  

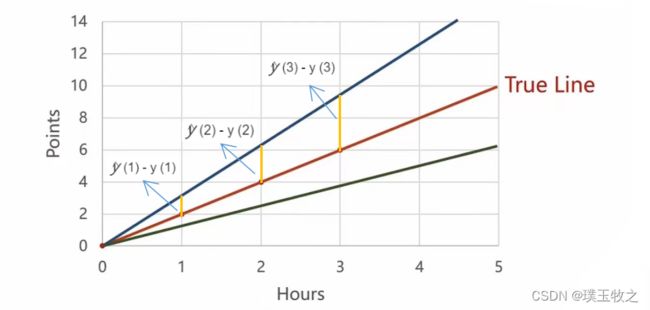
2.2.2 找最优权重（不同权重的直线的倾斜角度不同）

• The machine starts with a random guess, w = random value

• 先取随机数，再评估。在选取了一个权重后，看它所表示的模型和数据集里的数据之间的偏移程度有多大
  

• 计算 $\hat{y}$ (1) - y (1)、$\hat{y}$ (2) - y (2)、$\hat{y}$ (3) - y (3)。若选取的模型非常接近True Line，则这三个值的平方和是很小的。

• 所以要寻找一个评估模型，看模型和数据集里的数据之间的误差有多大，这个评估模型在机器学习中叫做Loss。

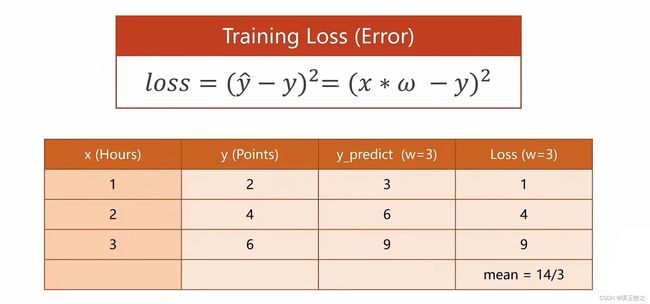
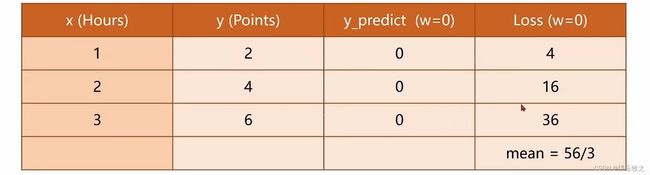
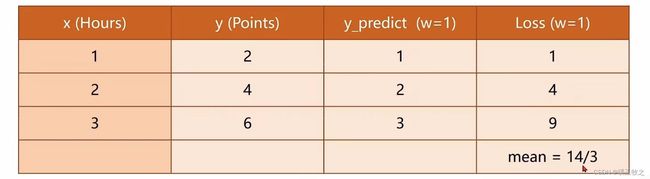
2.2.3 Training Loss

最终目标是找到一个权重值，使平均损失mean降到最低

• 假设 w = 3，结果如上图所示，平均损失mean=14/3

• 假设 w = 4，结果如下图所示，平均损失mean=56/3
  

• 假设 w = 0，结果如下图所示，平均损失mean=56/3
  

• 假设 w = 1，结果如下图所示，平均损失mean=14/3
  

• 假设 w = 2，结果如下图所示，平均损失mean=0
  

• 损失函数是针对一个样本的，对于整个Training set损失，需要把每一个样本的预测值和真值之间的差值平方相加，再除以样本总数，就得到了平均平方误差 (MSE: Mean Square Error)。

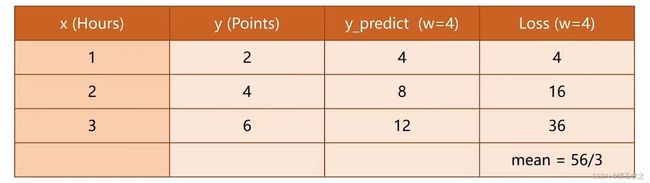
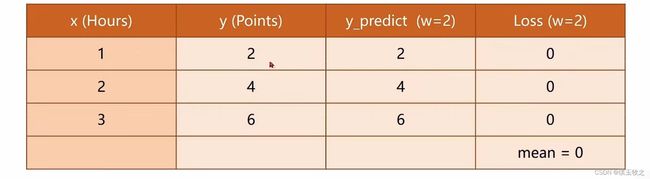
2.2.4 MSE

• 计算各个平均平方误差：
  

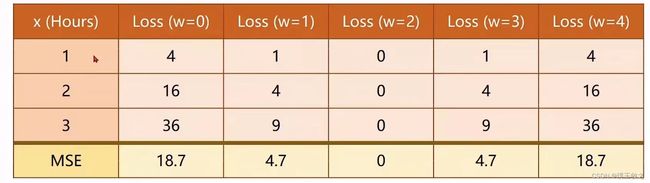
有时并不能保证算出0，所以需要考虑取哪些值作为 w 的候选值，由于并不能确定在这些候选值中能得到最优权重，所以需要用到穷举法。

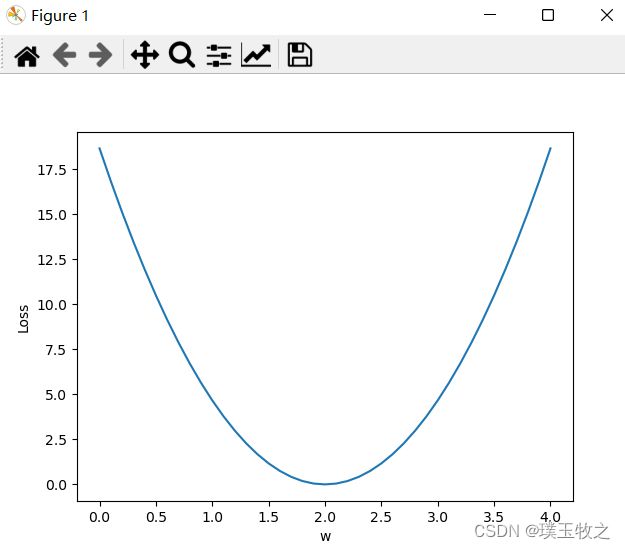
穷举法：例如，经过测试发现在0-4之间，存在损失最小的权重，那么就把0-4之间所有可能的取值都计算出损失，得到下图的曲线，曲线的最低点，就是损失的最优权重。

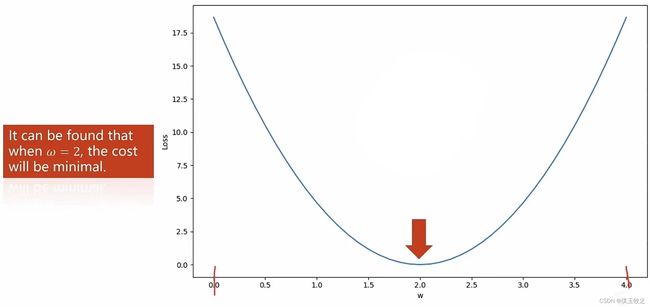
2.3 代码实现

import numpy as np
import matplotlib.pyplot as plt

x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]   #输入数据集（相同索引对应一组样本）

def forward(x):            #定义模型（前馈），线性模型 Linear Model
    return x * w

def loss(x, y):            #定义损失函数 Training loss
    y_pred = forward(x)    #求y_hat
    return (y_pred - y) * (y_pred - y)

w_list = []                #权重列表
mse_list = []              #平均平方误差列表
for w in np.arange(0.0, 4.1, 0.1):           #从0到4取值，间隔为0.1
    print('w=', w)
    l_sum = 0
    for x_val, y_val in zip(x_data, y_data):
        y_pred_val = forward(x_val)          #预测值
        loss_val = loss(x_val, y_val)        #计算损失
        l_sum += loss_val                    #将损失求和
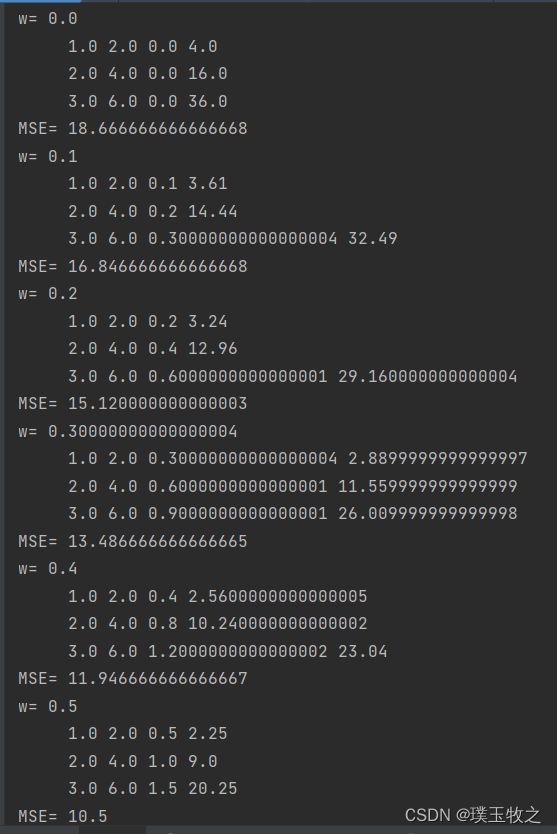
        print('\t', x_val, y_val, y_pred_val, loss_val)
    print('MSE=', l_sum / 3)                 #出样本总数，转换成MSE
    w_list.append(w)
    mse_list.append(l_sum / 3)


#Draw the graph
plt.plot(w_list, mse_list)
plt.ylabel('Loss')
plt.xlabel('w')
plt.show()

2.4 结果截图

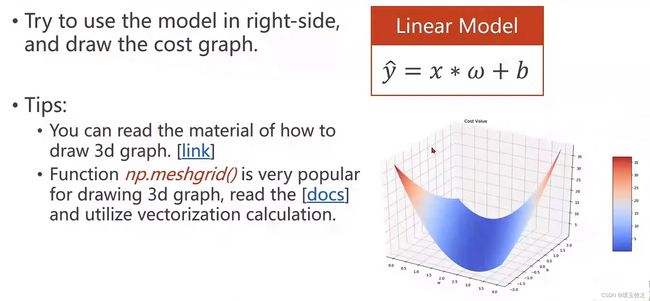
3.Exercise

3.1 代码实现

import numpy
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import cm
from mpl_toolkits.mplot3d import Axes3D

x_data = [1.0, 2.0, 3.0]    #输入数据集y=x*2.5-1
y_data = [1.5, 4.0, 6.5]

def forward(x):             #定义模型（前馈）
    return x * w + b

def loss(y_pred, y):        定义损失函数
    return (y_pred - y) * (y_pred - y)

w_list = np.arange(0.0, 4.0, 0.1)     #权重列表
b_list = np.arange(-2.0, 2.1, 0.1)    #b
w, b = numpy.meshgrid(w_list, b_list, indexing='ij') #将w,b转换为二维矩阵

mse_list = [] #平均平法误差列表
l_sum = 0.
for x_val, y_val in zip(x_data, y_data):
    y_pred_val = forward(x_val)
    loss_val = loss(y_pred_val, y_val)
    l_sum += loss_val
mse_list.append(l_sum/3)


#Draw the graph
fig = plt.figure(figsize=(10, 10), dpi=300) #设置分辨率和画布大小,分辨率参数-dpi，画布大小参数-figsize
ax = Axes3D(fig)#将figure变为3d
# 绘图，rstride:行之间的跨度  cstride:列之间的跨度
surf = ax.plot_surface(w, b, np.array(mse_list[0]), rstride=1, cstride=1, cmap=cm.coolwarm, linewidth=0, antialiased=False)
# Customize the z axis.
ax.set_zlim(0, 40)
# 设置坐标轴标签
ax.set_xlabel("w")
ax.set_ylabel("b")
ax.set_zlabel("loss")
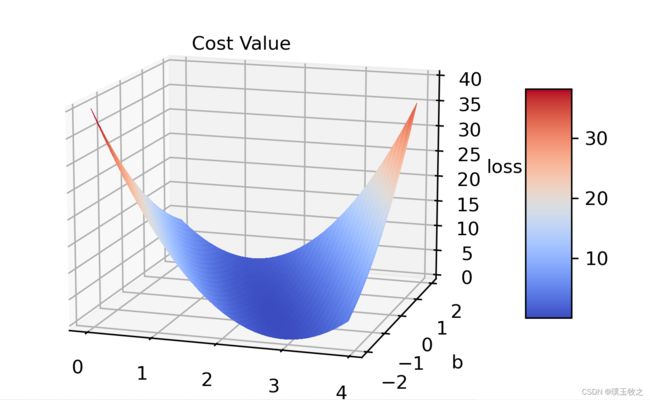
ax.text(0.2, 2, 43, "Cost Value", color='black')

fig.colorbar(surf, shrink=0.5, aspect=5) #设置颜色
plt.show()

3.2 结果截图

本文参考：《PyTorch深度学习实践》