论文翻译——Multi-Constrained Graph Pattern Matching in Large-Scale Contextual Social Graphs

Abstract

• 摘要：图模式匹配（Graph Pattern Matching，GPM）在社交网络分析中发挥着重要作用，广泛应用于专家搜索、社会社区挖掘和社会地位检测等领域。给定模式图 GQ 和数据图 GD，GPM 算法会找到与 GD 中的 GQ 匹配的子图 GM 。然而，现有的 GPM 方法没有考虑 GQ 中边缘的多重约束，这些约束普遍存在于各种应用中，例如众包旅游、基于社交网络的电子商务和研究组选择等。
• 在本文中，我们首先在概念上将有界模拟扩展到多约束模拟 (MCS)，并提出了一个新的 NP 完全问题，多约束图模式匹配 (MC-GPM) 问题。然后，为了解决大规模 MC-GPM 中的效率问题，我们提出了一个名为强社会成分 (SSC) 的新概念，由具有强社会关系的参与者组成。我们还提出了一种识别 SSC 的方法，并提出了一种新的索引方法和 SSC 的图压缩方法。此外，我们设计了一种启发式算法，无需解压缩图形即可有效且高效地识别 MC-GPM 结果。对五个真实世界的大规模社交图的广泛实证研究证明了我们方法的有效性、效率和可扩展性。

附加

• 目前很少有算法考虑到点和边的多约束模拟，作者提出新的模拟，多重约束模拟
• 创建“强社会成分（SSC）”的新概念，以及相应的识别算法，然后还有对应索引方法和SSC图压缩方法
• 设计一种启发式算法，无需解压图片，就可以识别MC-GPN结果，并在五个真实社交图中进行验证

Introduction

Background

• 在线社交网络 (OSN) 吸引了全球数十亿用户，为用户执行各种任务提供了丰富的信息，例如检测社会地位 [1]、寻找专家 [2]、[3] 和制定旅行计划 [2]。这些任务通常是通过应用已广泛用于社交网络分析的图形模式匹配 (GPM) 来执行的。 GPM 通常根据子图同构来定义，其中，给定数据图 GD 和模式图 GQ 作为输入，它会回答 GD 是否包含与 GQ 同构的子图。

• Example 1

  • 样例包括了：三个查询图GQ1，GQ2，GQ3和四个数据图GD1，GD2，GD3，GD4
    

• GQ1对于GD1而言，是严格同构的，但是对于别的图并不是严格同构。传统的子图匹配都是严格同构的，过于严格了，在现实世界的社交网络中，很少能匹配到严格同构的。除此之外，子图同构问题本身就是NP完全的时间复杂度，很难将同构测试应用到大型社交网络中。

• 为了解决上述子图匹配的问题，提出了图模拟，他需要更少的约束，但是能够更有效地提取出更有用的子图。与子图同构相反，图模拟支持的是模拟关系，与子图同构中提取点匹配完全不同。在图1中，GQ1与GD2并不是同构的，但是如果通过图模拟进行子图匹配，则GQ1和GQ2是匹配，因为GQ1中的两B和C两个点，是以GD2中的B和C两个点一一相对应的。图模拟已经被广泛用于结构索引和网络分类，但是他仍旧需要边和边的匹配。对于通过设定路径长度的定点对连接的应用来说，这个限制仍旧太过严格。比如说GQ2中路径长度分别为2、3和※（表示无穷）。这主要用于可达性查询和模式匹配等应用中。

• 为解决图模拟中这一类问题，Fan等人提出了有界模拟，其中每一个顶点都有一个类别的标签，每一个边都有k或者※的表示长度的标记。基于有界模拟的图匹配是将模式图中边和数据图中有界长度的路径进行匹配的，这与单纯的图模拟和同构中的边对边匹配不同的。在图1中，如果使用有界匹配，那么GQ2是与GD1、GD2和GD3匹配的。基于有界模拟的匹配的研究已经开展了很多，包括限制模拟结构、匹配不同的边的类型，还有提高基于有界模拟的子图匹配的效率。

附加

• NP完全问题：存在这样一个NP问题，所有的NP问题都可以约化成它，只要解决了这一个问题，所有相关的NP问题都可以解决。
  • P类问题：存在多项式时间算法的问题，在多项式之内可以解答的问题
  • NP问题：能在多项式时间内验证出一个正确解的问题，这个问题不一定在多项式时间内可解，但可以在多项式时间内验证
  • NP-hard问题：所有的NP问题都可以规约到这个问题。
  • 约化/规约：问题A可以约化为问题B，称为“问题A可规约为问题B”，即问题B的解，
  • 
• 限制模拟结构：restrict the simulation structure
  • S. Ma, Y. Cao, W. Fan, J. Huai, and T. Wo, “Capturing topology in graph pattern matching,” in VLDB’11, pp. 310–321
• 在不同边的类型下进行匹配match with different edge types
  • W. Fan, J. Li, S. Ma, N. Tang, and Y. Wu, “Adding regular expressions to graph reachability and pattern queries,” in ICDE’11, pp. 39–50
• 提高基于的有界模拟子图匹配的效率
  • W. Fan, X. Wang, and Y. Wu, “Diversified top-k graph pattern matching,” in VLDB’14.
  • W. Fan, X. Wang, and Y.Wu, “Answering graph pattern queries using views,” in ICDE’14, pp. 184–195.

Problem

• 基于有界模拟的GPM在匹配边时，仅仅考虑了一条边的有限路径长度，贪婪寻找最短路径的子图。但是，一些路径在顶点和边上，都有不同的属性，比如说上下文社交图（Contextual Social Graph——CSG），在上下文社交图中，每一个顶点都有对应社会角色信息，每一个边都有社会关系和社会信任信息。在社交网路的不同应用中，比如说组团旅游、学习小组的选择和基于网购的社交网络，人们更加乐意于考虑到CSG中涉及的边的不同的社交上下文，因为这对于人们相互之间进行合作和做决定，有十分重要的作用。
• 样例二：考虑到图一中的GD4和GQ3，其中除了传统的结构，GD4中的每条边多有两个属性：a和b分别表示CSG中人与人之间的社会信任度和社会关系。关于CSG中现实应用，社会信任度（在GQ3中a >m）和社会关系（在GQ3中bm或者b
• 这个样例解释了一种新类型的多种约束子图匹配（Multi-Constraint GMP MC-GPM），其在社交网络中是十分重要的应用。MC-GPM包含了经典的NP-完全多种约束路径选择问题，所以其本身也是一个NP完全问题。所以，我们工作的主要挑战就是设计一个新的索引结构和近似技术，以高效和有效地支持MC-GPM查询。据我们所致，现存的所有GPM方法都是不支持MC-GPM查询的，我们贡献将在下一部分进行总结。

附加

• Crowd-sourcing travel众包旅游，组团游：R. Milano, R. Baggio, and R. Piattelli, “The effects of online social media on tourism websites,” in ITTT, 2011, pp. 471–483.
• 基于电子商务的社交网络Social network based e-commerce：G. Liu, Y. Wang, and M. A. Orgun, “Optimal social trust path selection in complex social networks,” in AAAI’10, 2010, pp. 1391–1398.
• 合作和做决定：G. Liu, Y. Wang, and M. A. Orgun, “Social context-aware trust network discovery in complex contextual social networks,” in AAAI’12, 2012.
• NP-Complete multi-constraint path selection problem：NP完全多重约束路径选择问题：J. M. Jaffe, “Algorithms for finding paths with multiple constraints,” Networks, vol. 14, pp. 91–116, 1984.，这个参考文献对于解决多重约束问题具有十分重要的意义
• to the best of our knowdge：据我们所知

Contribuitions

• （1）我们通过扩展有界模拟，提出了多重约束模拟的新概念（Multiple-constraint Simulation MCS）。与传统的模拟相比，基于多重约束的子图匹配的目标是寻找一个匹配结果，其中匹配子图的每一条边同时满足边的特定路径长度和边上的多重约束，这样能够更好地支持很多最新出现的社交网络应用.
• （2）我们提出了一种叫做强社会组成的概念（Strong Social Component SSC），由具有强大社会联系的参与者组成。同时我们提出了一种新的方法去识别SSCs。因为SSCs中的社会联系在很很长一段时间内都保持稳定，我们提出了一种针对的SSC的新的索引结构和图压缩算法，这种算法能够在多项式时间复杂度内实现。我们的方法能够在不解压的情况下，匹配模式图，借此能够减少存储消耗和改善效率。
• （3）我们使用了五个大型的现实世界的社交网络图，去做一个广泛性的经验研究，证明了我们提出的算法的有效性、高效率和可扩展性
• 文章的余下部分，会以如下的方式进行组织。我们首先在第二部分总结关于子图匹配的相关研究工作。然后我们在第三部分引入必要的概念，并且阐述本文的关键问题。在第四部分，我们介绍了强社会组成部分的识别，然后就是分别在第五节和第六节介绍图压缩方法和索引结构。第七部分，将会说明我们提出的MC-GPM算法，第八部分将会对实验观察进行汇报，第九部分对文章进行总结。

附加

• SSCs中的联系保持稳定：P. Berger and T. Luckmann, The Social Construction of Reality: A Treatise in the Sociology of Knowledge. Anchor Books, 1966.

Related Work

（1）

• 在学术界，图匹配方法已经被广泛研究，主要分为（1）基于同构的图匹配，这个是精确匹配GQ中的顶点和边，（2）基于模拟的子图匹配，这个是模拟GQ中的顶点和边，我们将在下面这个部分对其进行详细分析
• **Isomorphism-Based GPM：**在基于图同构的子图匹配的研究中，Zou 等人提出在数据图中任意两个端点之间最短路径长度创建了索引，以支持连接长度的要求。除此之外，Sun等人在子图匹配中使用图探索方法去提高子图链接操作效率。进一步，还有Cheng等人提出的Top-K子图匹配方法，其构建了一个用于循环图查询的生成树，并且对结果，依据器答案的边长度之和，进行排序。
• 给出一个查询图GQ，一般来说，直接找到严格匹配的图同构子图是不现实的。Yan等人提出了基于相似性的方法，在该方法中，距离是基于查询图和数据图之间匹配边的总数进行计算的。如果距离是小于特定的阈值，那么结果就可以返回。Shang等人进一步对Yan等人提出的方法进行改良，主要是根据数据图GD对于查询图GQ中特征的相似程度对图重建索引，借此来排除没有任何匹配可能的图。更进一步，Zhu等人将数据图划分为若干组相似的图，并且对这些图进行索引，来去除那些不可能匹配上的没希望的分支。
• 为了提高在大规模图中子图匹配的效率，学术界最近提出了并行和分布式的方法。在Zhu和Afrati等人提出方法中，一个模式图被分解为几个小的模板，然后他们寻找针对较小模板匹配子图，最后再将中间结果进行拼接，然后返回。除此之外，Shao等人提出了基于并行框架的多重子图回答。除此之外，在Huang等人的研究中，大数据图被分解为若干小的部分，然后进行分布式子图匹配，最后预测每一部分获得子图匹配答案的概率。

附加

• Zou等人，最短路径重建索引并进行连接：L. Zou, L. Chen, and M. T. Ozsu, “Distance-join: Pattern match query in a large graph database,” in VLDB’09, pp. 886–897.
• Sun图探索方法提高子图匹配效率：Z. Sun, H. Wang, H. Wang, B. Shao, and J. Li, “Efficient subgraph matching on billion node graphs,” in VLDB’12, pp. 788–799.
• Cheng等人提出的Top-K方法创建生成树进行匹配排序：J. Cheng, X. Zeng, and J. X. Yu, “Top-k graph pattern matching over large graphs,” in ICDE’13, pp. 1033–1044
• Yan提出的基于近似的方法：X. Yan, P. S. Yu, and J. Han, “Substructure similarity search in graph databases,” in SIGMOD’05, pp. 766–777.
• Shang等人提出基于特征相似度对图片进行索引，提高匹配可能性：H. Shang, X. Lin, Y. Zhang, J. X. Yu, and W. Wang, “Connected substructure similarity search,” in SIGMOD’10, pp. 903–914.
• Zhu和Afrati提出的将图分为若干小图，分开找然后合并成一个大图：F. N. Afrati, D. Fotakis, and J. D. Ullman, “Enumerating subgraph instances using map-reduce,” in ICDE’13, pp. 62–73.
• Shao等人使用并行框架进行子图匹配：Y. Shao, B. Cui, L. Chen, L. Ma, J. Yao, and N. Xu, “Parallel subgraph listing in a large-scale graph,” in SIGMOD’14, pp. 625–636.

（2）

• Simulation-Based GPM：因为基于图同构的子图匹配对于大部分应用来说，仍旧过于严格，所以有人提出了基于图模拟的子图匹配。Fan等人提出了基于有界模拟的子图匹配，其中每一个顶点的标签并不是唯一的，并且在查询图中每一个边都会指定有界长度。在有界模拟中，并不需要像子图同构一样，严格匹配每一个顶点和边，相反，在有界模拟中，定点只需要具有相同的标签就可以实现顶点匹配，路径的长度只要不大于数据图中有界长度就可实现路径匹配。这种类型的子图匹配只需要在立方时间内就可以实现。除此之外，基于有界模拟，Me等人提出了名为“强模拟（Strong Simulation）”的方法，其目标是找到比起有界模拟，其拓扑结构与查询图更加相似的匹配集合。此外，Fan等人考虑到要满足子图匹配中边的不同类型，提出了新的方法。此外，为了提高效率，Fan等人基于有界模拟提出了一个图模式视图（？？不是很懂），其中在数据图中定义一组视图，并提出一中估计方法，用来预测那个视图能够回答特定的查询。除此之外，他们还提出资源有限查询，提取出最有可能包含查询图的匹配结构的那部分图。最后，Fan等人还提出了针对特定顶点模式的Top-K个匹配的方法，其中包含重要顶点和边的模式，在查询图中最有高优先级进行优先匹配。

附加

• Fan等人提出了基于有界模拟的子图匹配：W. Fan, J. Li, S. Ma, N. Tang, Y. Wu, and Y. Wu, “Graph pattern matching: From intractable to polynomial time,” in VLDB’10, pp. 264275.
• Me等人提出了名为“强模拟（Strong Simulation）”的方法：S. Ma, Y. Cao, W. Fan, J. Huai, and T. Wo, “Capturing topology in graph pattern matching,” in VLDB’11, pp. 310–321.
• Fan等人考虑到要满足子图匹配中边的不同类型：W. Fan, J. Li, S. Ma, N. Tang, and Y. Wu, “Adding regular expressions to graph reachability and pattern queries,” in ICDE’11, pp. 39–50
• Fan等人提出基于有界模拟的视图匹配：W. Fan, X. Wang, and Y.Wu, “Answering graph pattern queries using views,” in ICDE’14, pp. 184–195.
• 资源有限查询：W. Fan, X. Wang, and Y. Wu, “Querying big graphs within bounded resources,” in SIGMOD’14, pp. 301–312
• Fan等人还提出了针对特定顶点模式的Top-K个匹配的方法：W. Fan, X. Wang, and Y. Wu, “Diversified top-k graph pattern matching,” in VLDB’14.

（3）

• Summary：基于图同构的子图匹配在很多应用中很重要，比如说3D模型匹配和蛋白质结构匹配。索引、并行和分布式方法是提高子图匹配效率十分有效的方法。然而，这样的子图匹配代价十分高昂，因为这是一个NP完全问题。然而，尽管基于相似的方法已经提高返回答案的可能性，但是仍旧是太复杂了，以至于在很多应用中都用不了，比如说找到社会专家和组织项目。基于模拟的子图匹配放宽了子图同构的约束，因而很好的解决了这些应用中的子图匹配难题。但是所有现存的方法都没有考虑到图查询中的边上的多重约束。在很多基于社交网络的应用中，这种查询十分普遍和基础，这类应用包括组团旅游、学习小组选择和基于电子商务的社交网络。因此当前的子图匹配算法并不支持很多应用中的多重约束子图匹配。

附加

• 组团旅游应用Crowd-sourcing travel：R. Milano, R. Baggio, and R. Piattelli, “The effects of online social media on tourism websites,” in ITTT, 2011, pp. 471–483.
• 基于电子商务的社交网络Socila network based e-commerce：G. Liu, Y. Wang, and M. A. Orgun, “Optimal social trust path selection in complex social networks,” in AAAI’10, 2010, pp. 1391–1398.

Preliminaries

A Data graph数据图

• 1）上下文社交网络图：一个上下文社交网络图（CSG）是一个带标记的有向图G=（V，E，LV，LE），其中
  • V 是顶点集
  • E 是边的集合，（Vi，Vj）∈E表示一个有向边从顶点Vi指向Vj
  • LV是定义在顶点集V上的函数，对于顶点集V中的每一个顶点v，LV（v）是顶点v的标签集合。通俗的说，定点标签可能表示顶点在某一个领域的社会角色。
  • LE是定义在边集合E上的函数，对于E中任一条边（Vi，Vj），LE（Vi，Vj）都是边（Vi，Vj）集合的标签，比如说在特定领域的社会关系和社会信任程度。
• **Example 3 **：我们现在给出一个上下文社交图的特定样例，去展示顶点和边的标签定义和使用的过程。看上图2的GD5就是一个上下文社交图，其中点集V中的每一个顶点vi都和一个角色影响因子关联，表示为ρDivi∈[0,1]，表示参与者vi在领域i的影响，这是由节点vi的专业知识决定的。如果ρDivi=1表示vi在领域i内是一个领域专家，相反的，如果ρDivi=0表示vi在领域i内一无所知。除此之外每一个边（vi,vj）都和社会信任程度相关，表示TDivi，vj∈[0,1],还有社会亲密程度，表示为rvi,vj∈[0,1]，表示参与者之间的信任和社会亲密关系。T，r和ρ都是社会影响因子，他们值都可以使用数据挖掘技术进行的提取。
• 基于社会心理学的理论，我们采用乘法去聚合一个路径的T和r的值，采用平均的方法去聚合路径上顶点的ρ的值。聚合方法具体细节，见附加中“CSG上下文社交图”这篇参考文献。路径p在领域i的聚合值表示为ASDi ( p) ={ATDi ( p),ArDi( p),AρDi ( p)}，如果路径p的每一个聚合社会影响因素值都比路径p‘中每个对应值都大，那么在领域i，路径p是支配路径p’的，表示为

附加

• CSG上下文社交图：G. Liu, Y. Wang, and M. A. Orgun, “Optimal social trust path selection in complex social networks,” in AAAI’10, 2010, pp. 1391–1398.
  • 在后续如果要解释算法，还是需要使用这个东西，所以要了解一下。

B. Patttern Graph模板图

• 一个模板图被定义为GQ=（V_q,E_q,f_v,f_e,s_e），其中
  • V_q,E_q分别表示顶点集和边集
  • f_v是定义在V_q上的函数，对于每一个顶点u，f_v(u)是u的定点标签。
  • f_e是定义在边集合E_q上的函数，对于每一个边（u，u’），f_e（u，u’）表示边（u，u’）的有界长度，可以是正整数k也可以是符号*
  • s_e是一个定义在E_q上的函数，对于每一个边（u，u’）,s_e（u，u’）表示路径（u，u’）上的聚合社交影响因子值的多重约束，通过λ^Di_T,λ^Di_ρ和λ_r，他们的范围都是[0,1].
• 在图二中GQ4，我们能看到多种约束，比如说边（B，C）上的λ^Di_T,λ^Di_ρ和λ_r

C Multi-Constraint Graph Pattern Matching（MC-GPM）

• 在这部分，我们将通过CSGs多重社交网络中多重约束来引进（MC-GPM）多重约束子图匹配。
• Bounded Simulation 【2】：给一个数据图G=（V，E，LV）和一个查询图Q=（V_q,E_q,f_v,f_e）。如果说一个数据图G在有界模拟上匹配查询图Q，记为，需要存在一个二元关系S$\subseteq$V_Q×V，这个二元关系具体描述如下
  • 对于所有查询图中所有的顶点u，在数据图的顶点集V中存在v，而这构成的二元关系（u，v）属于二元关系S
  • 对于二元集中的每一个二元对（u，v）
    • 顶点u和顶点v是等价的
    • 对于查询图Q的边集中每一条边（u，u’），在数据图G中存在非空路径p，该路径是从顶点v到v’，同时二元关系（u’,v’）也属于二元关系集S。并且如果在查询图中边（u，u’）为k，那么在数据图中路径p的长度也要小于等于k
• 然后有序对集S就是通过有界模拟，数据图G中对于查询图中Q的匹配结果。
• Multi-Constraint Simulation （MCS）：MCS是有界模拟的非平凡扩展。现有一个数据图G_D=（V，E，LV，LE）和一个匹配查询图G_Q=（V_q,E_q,f_v,f_e,s_e）.如果存在一个二元关系S $\subseteq$V_Qx V, G_D通过MCS匹配G_Q，表示为,这个二元关系的具体描述如下：
  • 对于查询图Q中的任意顶点u，在数据图中都存在与之相对应的顶点v，二者构成二元关系（u，v），都属于关系集合S
  • 对于S中的任意顶点对，都满足如下的关系
    • 查询图G_Q中的顶点u和数据图G_D中对应的顶点v是等价的，数学描述为u~v
    • 对于查询图Q的边集中每一条边（u，u’），在数据图G中存在非空路径p，该路径是从顶点v到v’，同时二元关系（u’,v’）也属于二元关系集S。并且如果在查询图中边（u，u’）为k，那么在数据图中路径p的长度也要小于等于k
    • 如果查询图任意一边（u，u’）的约束因子为S_e(u,u’)={λ_T,λ_T,λ_T}，那么数据图中对应边的聚合值要满足对应条件，即AT^D_i (v,v’) ≥λ_T,Ar (v,v’) ^D_i≥λ_r,Aρ (v,v’) ^D_i≥λ_ρ
  • 然后S就是基于多重约束的匹配结果
• 如果查询图G_Q中边（u，u’）基于MCS，被映射为数据图G_D中一个从顶点v到v’的非空路径p，那么数据图G_D中的路径（v,v’）就是一个边模式匹配，表示为，并且（u，v）是属于有序对集合S的，这种匹配及作为（v，v’，G_D）
  （u，u’，G_Q）。如果对于G_Q中每一个边，在数据图中都有对应匹配的边，那么一个多约束子图匹配问题的答案就有了，记作
• Example 4：假设图2中的G_Q4是用户给出一个查询，从上下文社交图中找出一组合作者去完成项目。基于数据图G_D5，我们能够获得多重约束子图匹配（MC-GPM）的答案为
  • （1）在查询图G_Q4中的顶点SPM（A，是一个高阶项目经理）和顶点PM（B是一个项目经理）能够被映射到数据图G_D5中相同顶点SPM和PM，着已经满足了子图同构的一部分。
  • （2）查询图G_Q4中顶点AM（助手经理）对于G_D5中的多个AM点（C₁和C₂），这种关系可以使用图模拟进行确定
  • （3）查询图G_Q4中的有限路径长度的边，已经使用有界模拟，映射为G_D5中已经特定长度的路径。
  • （4）多重约束的边，使用多重约束模拟，能够映射为数据图G_D5中特定聚合社会影响因子值得路径。

D. A Baseline Algorithm

• 因为现存并没有任何方法能够解决多重约束子图匹配问题，并且多重约束是有界模拟的一个扩展，在这部分，我们将引入一个基础方法，通过有界模拟扩展子图匹配算法。具体细节如下
• step 1：对于查询图G_Q中每一个被约束的边，在数据图G_D中计算被匹配的最短路径长度，Slen（p）
• step 2：如果路径p的长度slen§小于等于查询图中对应边的有界长度（记作Blen），即Slen（p）≤Blen（p），就进一步判断路径p的聚合社会影响因子的值是否能满足的相关约束
  • 如果每一个约束都可以被满足，那么就返回边的匹配结果
  • 否则，基于Top-K路径选择算法，计算长度第二段的路径，并重新运行步骤二
• step 3：在研究过查询图G_Q中所有的边之后，如果有查询图中每一条边都有相应的匹配结果，那么通过子图匹配算法返回最终的结果（具体详见第七部分B）。否则的话，在数据图G_D中就没有匹配结果

附加

• Top-K算法：D. Eppstein, “Finding the k shortest paths,” SIAM Journal on Computing, vol. 28, no. 2, pp. 652–673, 1999

Example 5

• 考虑一下在图二中子图匹配案例，基线算法能够返回边匹配结果，（A，C₁，G_D5）等价于（A，C，G_Q4），（A，C₁，G_D5）等价于（A，D，G_Q4）。然后返回查询图G_Q4中边（B，C）的边匹配答案，（A，C₂，G_D5）等价于（B，C，G_Q4），（A，C₂，C₁，G_D5）等价于（A，C，G_Q4），边（B，D）的匹配结果是（A，C₂，C₁，G_D5）等价于（B，D,G_Q4）.因为通过B，C₂，F和D的路径P并不满足相关边的约束，AT^{Di(P_{(B，C2，F，D)})＜0.6。因为对于查询图G_Q4中的每一条边，都至少有一条边与其相匹配，通过使用基于子图匹配的方法进行搜索，可以返回多重约束子图匹配的结果。最终匹配的图是G_M=(V，E，LV，LE)，其中V={A，B，C₁，C₂，D}，E={（A，C₁），（B，C₂），（C₂，C₁），（C₁，D）}}
• 假设对于查询图G_Q中的每一条边，基线算法都需要在数据图G_D上运行N次迪杰斯特拉算法，然后基线算法的时间复杂度就是O（E_Q N N_D logN_D + N E_Q E_D）

IV Strong Social Component

• 为了提高我们多重约束子图匹配方法的效率和效果，在这部分，我们将会介绍一种强社会组成部分（Strong Social Component）识别方法。在图论中，如果要说一个图G是强连通图，那么从图上任一个顶点出发，要能到达图中所有的顶点，并且有向图中的强连接部分的是这个图中某一部分子图是强连通的。基于强连通的定义，我们下面给出强社交网络组成的定义。
• Definition 1： Strong Social Component. 在上下文社交网络中，如果我们称一个子图是社交强连接的，那么该子图的每一个角色影响因子值很高的节点，要能够和子图中社会关系亲密并且社会信任关系强的边相连。一个强社会组成部分（SSC）是一个社交性强链接子图。
• Example 6：在一个强社会组成部分中，假设每个边和顶点相关的T、r和ρ值都应该大于0.8.图3，描述了一个图，他分别在领域 i 和领域 j 都有两个强社会组成部分（SSC），其中对应的T、r和ρ都大于0.8.

• 基于社会心理学理论，在强社会组成部分中，社交网络结构和社交上下文，包括边上的社会信任和社会关系，还有顶点相关的社会角色在很长时间内都十分稳定。这个属性使得以低更新成本去对SSC进行索引和压缩成为现实。
• 识别特定领域的所有的SSC，包括经典的NP完全求最大团的问题，这是一个十分耗时的问题。或者，对于MC-GPM多重约束子图匹配问题，我们的能够识别出K个SSCs（强社会组成部分）。我们提出一个SSC识别方法，这个算法的简单描述如下。首先我们随机选择K个顶点作为种子，这些顶点的角色影响因子值都很高。然后，从每一个种子节点出发，我们算法采取广度优先（BFS）方法去找到别的角色影响因子十分高的节点，二者之间的边上具有高社会亲密度和社会信任值。最差的样例中，我们的方法需要遍历数据图中所有的节点和边。该SSC识别算法的时间复杂度是O（N _D E_D），算法的伪代码展示在算法1中，详见下图。

附加

• NP完全求最大团问题：N. Biggs, E. Lloyd, and R. Wilson, Graph Theory. Oxford University Press, 1986.

V. Context-Preserved Graph Compression For SSC针对强社会组成部分的上下文保留图压缩

• 在这部分，基于当前针对有界模拟的图压缩算法，我们提出了一种上下文感知图压缩算法，该算法保证了图的可达性、匹配模式和社会上下文。而且，我们方法压缩过后的图，能够直接进行查询，不需要进行解压。相反的，现存的图压缩算法都不能用来解决多重约束子图匹配问题，并且他们并不能保存上下文社交信息。相反，现存的方法不得不在紧凑的结构中，保存原始的图信息，去回答的图匹配问题。

附加

• 基于当前针对有界模拟的图压缩算法：W. Fan, J. Li, X. Wang, and Y. Wu, “Query preserving graph compression,” in SIGMOD’12, pp. 157–168

A. Compression for Reachability

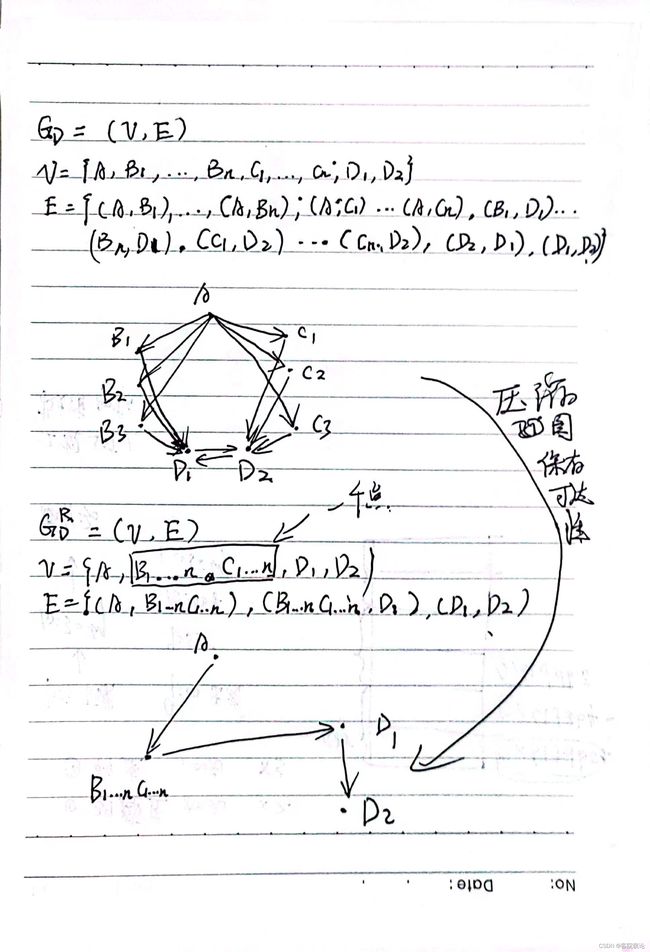
• 在查询图G_Q中检测任意顶点对的可达性，实际上是判断是否存在至少一个路径能够连接起在数据图中与查询图对应的两个顶点，比如说在图一中的查询图G_Q中的定点对（B，C）。通过定理捕获的图压缩属性，保留了可达性信息，称为可达性保留压缩，记作：G^R _D.

• 定理一：当被压缩的两个顶点具有相同的祖先并且可以到达彼此的后代，那么就说这个压缩图是保留了可达性。

• Proof：这段没有证明，公式太多，不是很好翻译，直接截图，主要是证明定理一.
  

• 对于图中给出的两张图而言，下图是上图的压缩，并且保留了可达性的压缩
  

• **Example 7 **：图4，包含了两组图，其中图4（a），数据图G _D7 是原始的数据图，G ^R _D7 是经过压缩之后的图。从数据图 G _D7 中，我们可以看到节点A和节点B并没有任何的祖先，但是有共同的后代节点（C、D和E）。因此节点A和节点B能够被压缩为压缩图G ^R _D7 中的一个节点，并且保存了其可达性。
  

B. Compression for Graph Pattern

• 压缩除了保存可达性，还要能支持图像模式匹配，比如说图二中查询图G _Q4 中的边（A，D），我们提出一种能够保存这一类图模式压缩算法。我们称之为图模式保存压缩，记作G^P _D ，该方法通过定理二进行证明。

• **Theorem 2 **：如果说一个被压缩的图是保存图模式的，那么被压缩的两个节点要具有相同的标记，相同的祖先和相同的后代

• **Proof：**证明就通过手写的照片，这里不翻译。

• Example 8：考虑图4中的样例，图四包含了一个数据图G _D8 ，以及相应的压缩图G ^P _D8 。在数据图G _D8 中，我们能看到B₁和B₂具有相同的祖先A和相同的后代C。因此，基于定理2，G ^P _D8 是G _D8 的保存了图模式的压缩图。

• Theorem 3：定理三，保存了图模式的压缩图，也保存原图的可达性。

• **Proof：**正如定理一和定理二解释的一样，保存图模式的压缩，比保存可达性的压缩更加严格。所以，定理三即可被证明。

C. Compression for Social Contexts

• 为了支持多重约束子图匹配，比如图2中查询图G_Q4中的边（B，D），我们提出的图压缩算法能够保存节点的上下文信息，表示为G^S _D。通过定理4能够证明压缩算法保存上下文的属性

• Theorem 4：定理4，如果说被压缩的图保存了上下文社交信息，那么被压缩的两个顶点要具有相同标签，相同祖先，相同后代，通过不同点的的路径，其中占据支配地位的聚合值要大。

• **Proof：**证明，请看下述手写过程，并没有贴具体的内容

• Example 9： 图5样例中包含了一个数据图G_D9 和相应的保存上下文社会信息的图G_D9 ^S，在数据图G_D9 中，我们能看到C₁和C₂ 具有相同的祖先A和相同的后代D。除此之外，基于定理4，C _D9

• Theorem 5

• Proof：

D. Summary

• 我们的图压缩方法能够保存上下文社交信息的重要信息，包括可达性、图模式和社交信息。因此，基于多重约束的子图匹配问题并不需要对图进行解压就可以解答。通过压缩上下文社交图中的顶点和边，能够节省运行内存和查询时间（具体详见实验细节）。除此之外，即使是最差的形况，我们的压缩方法也不过是浏览数据图中所有的顶点和边。因此，我们算法的时间复杂度是O(N _D E _D)。正如在第四部分提到的SSC（强社会组成部分）中结构和上下文社交信息在很长时间都是稳定不变的，因此不需要频繁更新已经压缩过的数据图。当SSC中结构或者上下文社交信息有所变化时，可以采用更加高效的增量图压缩算法。这些方法也主要是判断改变的这部分图是否会影响原先压缩的图片进行子图匹配，并且他们也仅仅是的重复压缩带来变化的那一部分子图，而不是重新压缩整个数据图。

附加

• 更加高效的增量压缩算法
  • 【10】W. Fan, J. Li, X. Wang, and Y. Wu, “Query preserving graph compression,” in SIGMOD’12, pp. 157–168.
  • 【33】W. Fan, X. Wang, and Y.Wu, “Answering graph pattern queries using views,” in ICDE’14, pp. 184–195

VI Index Of Strong Component

• 为了改良多重约束子图匹配的效率，我们提出了一种新的索引结构，对压缩图的可达性，图模式和上下文社交信息等重要信息进行索引。

A. Reachability Index

• 这个索引记录的是一系列在图中能够相互搜索到的节点，每一个节点的索引包含了当前节点的祖先节点和后继节点。
• Example 10：样例10，图六是一个索引的样例，是图3描述的图在领域j中强社会组成部分（SSC）的索引。从图中，我们能看到每一个顶点的索引，包括三个部分：分别是可达性索引，图模式索引和上下文社交索引。我们以顶点E为样例，因为他既有祖先，也有后代。顶点E的可达性索引记录的是他的祖先节点C和后继节点H。类似地，我们为图中每个其他节点构建可达性索引。
• 如果给一个可达性查询，比如说图1中的查询图G_Q3的边（B，C），如果SSC（强社会组成部分）包括了查询节点，我们可以立刻判定可达性，极大地节省了查询的处理时间。

B. Graph Pattern Index

• 在对可达性信息进行索引后，我们进一步对图片模式信息构建索引，来提高图模式查询到效率。这个索引记录的是图中强社会组成部分（SSC）的任意两个顶点之间的最短路径。
• Example 11：样例11。图6展示了图模式索引。对于顶点E，除了可达性信息的索引，图模式索引记录了从祖先节点的C到节点E，和从节点E到子节点H的的最短路径。类似地，我们为其他每个顶点构建了图模式索引。
• 现给一个没有边界长度的图模式查询（节点与边之间的可达关系），比如图2中查询图G_Q4中的边（A，D），基于图模式索引，我们能够判断是否索引路径长度比有界路径长度大，并因此有效解决查询。

C. Social Context Index

• 为了提高多重约束子图模拟的效率，我们构建了上下文社交索引去记录在数据图中匹配路径的最大社交影响因子的聚合值。如下是索引的具体细节。

  • 如果两个节点之间的任意路径的每一个聚合T、r和ρ的值都大于其他路径，我们对路径长度和对应聚合社交影响因子值创建索引。
  • 除此之外，我们再分别对T值最大的，r值最大的和ρ值最大的三个路径构建索引。

• Example 12样例12，图6展示了社交上下文索引。这里，我们将节点C为样例，在图中，总共有两条从C出发到其后继节点H的的路径，分别是P1（C，E，H）和P2（C，F，H）。因为路径P1的社会影响因子聚合值完全大于P2的聚合值，然后我们使用其对应社交影响因子去对路径P1去做索引，其路径长度为
  没有翻译完

• 现给出一个带有多重约束的图模式查询，比如说图2中查询图G_Q4中的边（B，D），基于上下文社交索引，我们能够快速判断在数据图中是否存在边模式匹配，同时还能节省查询的处理时间。

D. Summary

• 上述三个索引记录了强社交组成部分的图中重要的信息。现在给出一个多重约束子图匹配的查询，如果查询边的两个节点能被映射到的数据图中强社会组成部分中的路径，这个索引信息能够快速判断出是否存在边模式匹配，故而大量节省查询处理的时间（详见实验细节）。除此之外，在最差的情况下，我们需要运行发四次迪杰斯特拉算法，所以时间复杂度是O(N_D logN_D + E_D)。进一步说，正如在第四部分提到的，在强社交组成部分的图中的结构和社交上下文信息在很长时间段都保持稳定，因此，不需要很频繁地更新索引，着减少了维系索引的代价，除此之外，学术界关于索引更新的算法已经有了很多研究，这里就不在做讨论。

VII An Multi-Constrained Pattern Matching Algorithm

• 基于之前介绍的压缩过后的数据图和SSCs强社会组成部分中索引，我们针对多重约束子图匹配问题，提出了新启发式算法，叫做HAMC，该算法使用的是我们提出的新的启发式搜索策略。HAMC首先