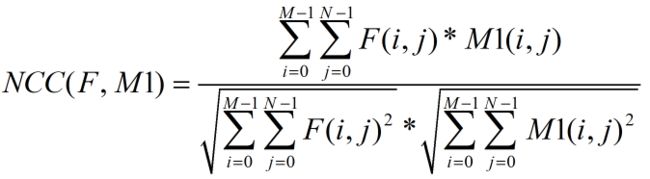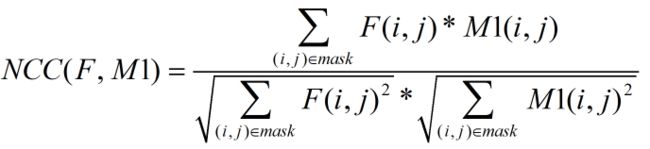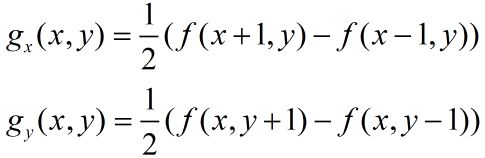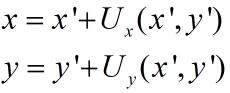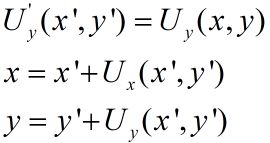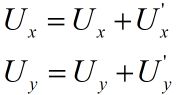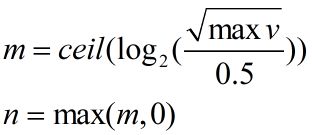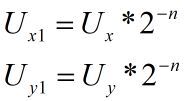微分同胚demons配准算法原理与C++/Opencv实现
01 前言
前文我们介绍过demons算法,以及在demons算法的基础上发展的Active demons算法和Inertial demons算法:
图像配准算法之demons算法![]() https://mp.weixin.qq.com/s/g2Wo9XrdDO7gDI7caV_IVg
https://mp.weixin.qq.com/s/g2Wo9XrdDO7gDI7caV_IVg
我们知道,demons算法是一种基于光流理论发展起来的配准方法,因此该算法与其它光流算法一样,具有小运动的约束条件。如果参考图像和浮动图像的差别很大,也即不满足小运动条件,那么demons算法的配准效果会很差。
为了解决小运动问题,Vercauteren T等人提出了微分同胚算法[1],将demons算法计算得到的位移场转换为微分同胚映射,从而对大运动或大形变都具有较理想的配准效果。本文介绍一种基于Active demons和微分同胚映射的大形变配准算法,其中使用到的微分同胚映射转换算法参考了Vercauteren T等人的文章。
首先我们来复习一下Active demons算法计算每个像素点位移的公式,其中其中Sx和Sy分别是参考图像上点(x,y)处x方向和y方向的梯度,Mx和My分别是浮动图像上点(x,y)处x方向和y方向的梯度,▽f则是点(x,y)处参考图像与浮动图像的灰度差: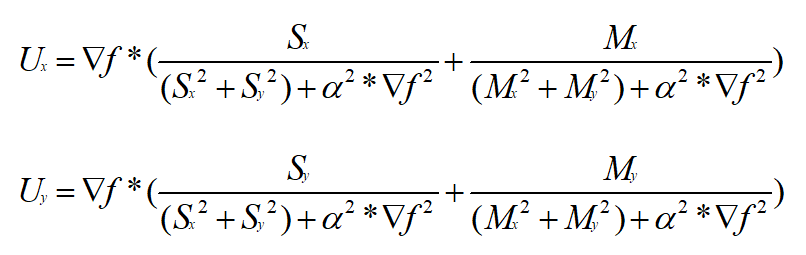
本文所介绍的微分同胚demons算法,则是在以上Active demons计算公式计算得到的Ux、Uy基础上,再将Ux、Uy转换为微分同胚映射。
02 什么是微分同胚映射?
微分同胚映射,它包含了“同胚”和“微分”两个条件,也就是说必须同时满足这两个条件的映射,才是微分同胚映射。下面我们分别介绍这两个条件。
-
同胚
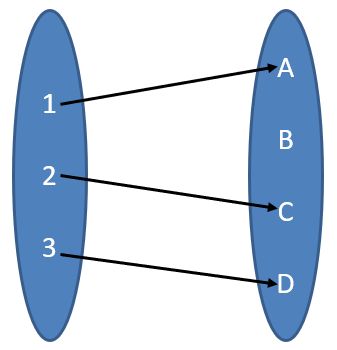
介绍同胚映射之前,我们先介绍一下数学中“单射”、“满射”、“双射”的概念。假设有函数y=f(x),函数f也可以称为从x到y的映射:
-
如果每个x值都有唯一的y值与之对应,那么映射f为单射。
-
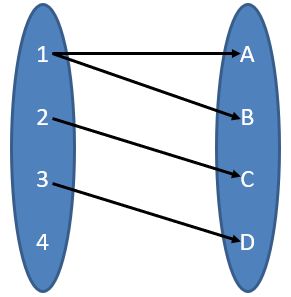
如果每个y值都至少有一个x值与之对应,那么映射f为满射。
-
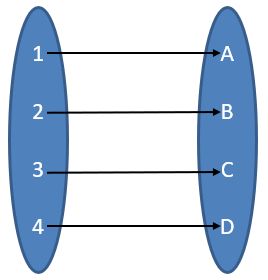
如果映射f同时满足单射和满射条件,那么又称之为双射,直观说就是当所有x值与所有y值一一对应的时候,映射f为双射。
单射、满射、双射的示意图如下:
单射非满射
满射非单射
双射
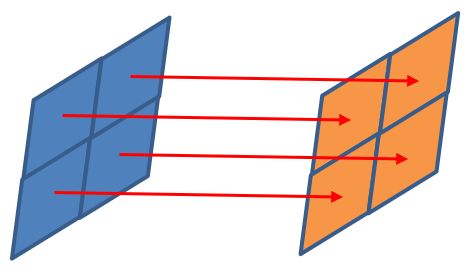
其实同胚映射跟双射是一样的,都是一一对应的关系,只是同胚映射通常用于形容拓扑空间的映射关系而已,比如对于两张图像,如果它们的所有像素点都满足一一对应关系,那么这个对应关系就是同胚映射,如下图所示:
同胚映射
-
微分
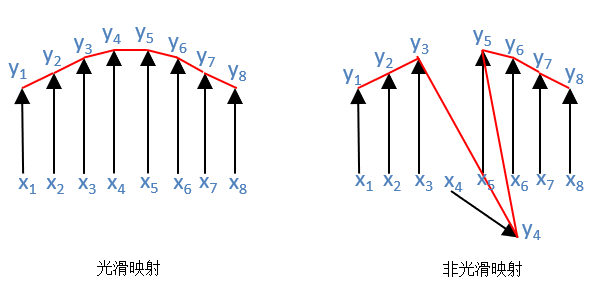
如果映射f满足以上所说的微分条件,意味着映射f与逆映射f-1都是光滑的映射。什么又是光滑映射呢?每个x值对应到y值的映射关系,与其邻域内其它x值对应到y值的映射关系是相似的,即使不完全一样,也是连续缓慢的变化,而不是突变,那么称x到y的映射为光滑映射。如下图所示,左图中x到y的映射是连续缓慢变化的,所以是光滑映射,而右图中x4到y4的映射,大小和方向都突变了,所以右图的映射不是光滑映射。
此处讲的光滑映射可能有点抽象,下文我们再举例更加直观地说明。
03 相似度衡量
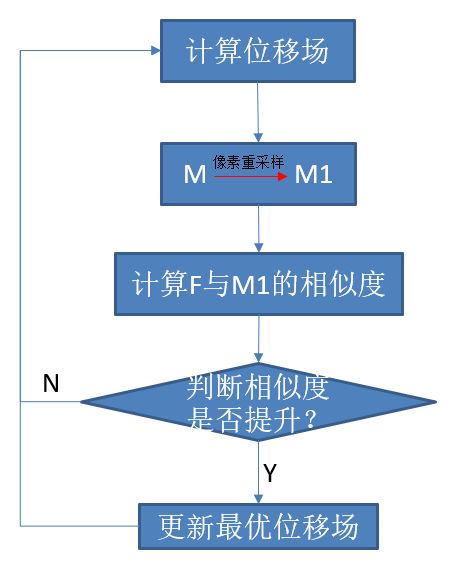
前文我们使用Active demons算法类配准的时候,每轮迭代都更新了最优位移场。实际上,并不是每轮迭代都是朝着配准效果更好的方向前进的,有的迭代配准效果反而更差,所以每轮迭代都更新最优位移场是有问题的。于是使用相似度来判断是否要更新最优位移场的方法被提了出来,流程如下图所示,其中F、M、M1依次为参考图像、浮动图像、像素重采样之后的浮动图像。
本文我们使用归一化互相关系数来衡量F、M1的相似度,假设F、M1都是M行N列矩阵,归一化互相关系数的计算公式如下:
NCC的取值范围0~1,NCC越接近1表示两张图像越相似。
考虑到在迭代过程中,图像M在像素重采样之后有可能会出现黑色边缘(例如下图),这些黑色边缘会影响相似度的准确性,所以计算NCC时应该把这些黑色边缘区域排除在外
我们首先根据计算的位移场获取黑色边缘的mask掩码矩阵,mask矩阵值为0的像素点属于黑色边缘,其它则不属于。假设每轮迭代计算得到的位移场为M行N列的矩阵Ux、Uy,对于每个像素点(x,y),判断其像素值是否满足以下条件(round为四舍五入运算),如果满足则判定点(x,y)不属于黑色边缘,并对mask(x,y)赋值255,反之则属于黑色边缘并对mask(x,y)赋值0。
基于以上得到的mask矩阵,NCC计算公式变成下式,也即只有非黑色边缘的点才加入计算,黑色边缘点排除在外:
04 梯度图的计算
计算位移场的时候,需要使用到参考图像F、浮动图像M的梯度。本文我们使用差分梯度来计算位移场。
对于图像上任意一点(x,y),其像素值为f(x,y),那么该点的x、y方向的梯度gx(x,y)、gy(x,y)可按下式计算:
按理说图像的边缘点没法按照上式计算梯度,所以我们需要对图像做边缘填充:在上、下各填充一行,左、右各填充一列。
例如,按照上式计算Lena图像所有像素点的x、y方向梯度,得到x、y方向的梯度图如下:
05 将位移场转换为微分同胚映射
这一步为微分同胚demons算法的核心。参考Vercauteren T等人的文章,可使用复合运算来实现近似微分同胚映射转换,那么什么又是复合运算呢?下面我们详细道来。
假设x、y方向的位移场分别为Ux、Uy,使用Ux、Uy分别对它们自身进行像素重采样的操作得到Ux'和Uy',然后再计算Ux+Ux'和Uy+Uy'的运算就是复合运算。对于Ux'的任意像素点(x',y'),其对应Ux上的点(x,y)的坐标可按下式计算:
得到(x,y)之后,再把点(x,y)的像素值Ux(x,y)赋值给Ux'上点(x',y'),即完成点(x,y)的像素重采样操作。
不过由于x、y都是浮点数,无法直接得到Ux(x,y)的值,所以本文使用双线性插值算法计算Ux(x,y)。关于插值算法与像素重采样的详细介绍,可参考前文:
常见图像插值算法的原理与C++实现![]() https://mp.weixin.qq.com/s/G9xXJKwuIHm4KyDndVKRxw
https://mp.weixin.qq.com/s/G9xXJKwuIHm4KyDndVKRxw
对Ux'的所有像素点都按照上述进行像素插值,则完成了从Ux到Ux'的像素重采样,从Uy到Uy'的像素重采样也同理:
最后再计算两者之和,即完成复合运算:
以上是复合运算的介绍,接下来就是将位移场转换为近似微分同胚映射的流程:
(1)按下式计算位移场Ux、Uy的平方和矩阵,其中“.*”为点乘运算,也即两个矩阵中对应位置的像素值相乘。
(2)求矩阵norm2的最大值maxv。
(3)按下式计算n,其中ceil为向上取整运算,比如ceil(1.1)=2.0,max为取较大值运算。
(4)计算矩阵Ux1、Uy1:
(5)对矩阵Ux1、Uy1作n次复合运算,最后结果就是近似的微分同胚映射。
06 微分同胚demons算法的代码实现
(1)计算梯度代码:
void get_gradient(Mat src, Mat &Fx, Mat &Fy)
{
Mat src_board;
//边缘扩充
copyMakeBorder(src, src_board, 1, 1, 1, 1, BORDER_REPLICATE);
Fx = Mat::zeros(src.size(), CV_32FC1);
Fy = Mat::zeros(src.size(), CV_32FC1);
for (int i = 0; i < src.rows; i++)
{
float *p_Fx = Fx.ptr(i);
float *p_Fy = Fy.ptr(i);
for (int j = 0; j < src.cols; j++)
{
p_Fx[j] = (src_board.ptr(i + 1)[j + 2] - src_board.ptr(i + 1)[j]) / 2.0 ;
p_Fy[j] = (src_board.ptr(i + 2)[j + 1] - src_board.ptr(i)[j + 1]) / 2.0;
}
}
} (2)复合运算实现代码如下,其中调用Opencv的remap函数可以方便地实现像素重采样。
//像素重采样实现
void movepixels_2d2(Mat src, Mat &dst, Mat Tx, Mat Ty, int interpolation)
{
Mat Tx_map(src.size(), CV_32FC1, 0.0);
Mat Ty_map(src.size(), CV_32FC1, 0.0);
for (int i = 0; i < src.rows; i++)
{
for (int j = 0; j < src.cols; j++)
{
Tx_map.at(i, j) = j + Tx.at(i, j);
Ty_map.at(i, j) = i + Ty.at(i, j);
}
}
remap(src, dst, Tx_map, Ty_map, interpolation);
}
//复合运算实现
void composite(Mat& vx, Mat& vy)
{
Mat bxp, byp;
movepixels_2d2(vx, bxp, vx, vy, INTER_LINEAR);
movepixels_2d2(vy, byp, vx, vy, INTER_LINEAR);
vx = vx + bxp;
vy = vy + byp;
} (3)微分同胚映射转换实现:
void exp_field(Mat &vx, Mat &vy, Mat &vx_out, Mat &vy_out)
{
Mat normv2 = vx.mul(vx) + vy.mul(vy);
double minv, maxv;
Point pt_min, pt_max;
minMaxLoc(normv2, &minv, &maxv, &pt_min, &pt_max); //求最大最小值
float m = sqrt(maxv);
float n = ceil(log2(m / 0.5));
n = n > 0.0 ? n : 0.0;
float a = pow(2.0, -n);
vx_out = vx * a;
vy_out = vy * a;
//n次复合运算
for (int i = 0; i < (int)n; i++)
{
composite(vx_out, vy_out);
}
}(4)高斯滤波函数实现,调用Opencv的函数GaussianBlur可方便实现高斯滤波:
void imgaussian(Mat src, Mat& dst, float sigma)
{
int radius = (int)ceil(3 * sigma);
int ksize = 2 * radius + 1;
GaussianBlur(src, dst, Size(ksize, ksize), sigma);
}(5)计算Active demons位移场的代码实现:
void demons_update(Mat S, Mat M, Mat Sx, Mat Sy, float alpha, Mat& Tx, Mat& Ty)
{
Mat diff = S - M;
Tx = Mat::zeros(S.size(), CV_32FC1);
Ty = Mat::zeros(S.size(), CV_32FC1);
Mat Mx, My;
get_gradient(M, Mx, My); //求M的梯度
float alpha_2 = alpha * alpha;
for (int i = 0; i < S.rows; i++)
{
float* p_sx = Sx.ptr(i);
float* p_sy = Sy.ptr(i);
float* p_mx = Mx.ptr(i);
float* p_my = My.ptr(i);
float* p_tx = Tx.ptr(i);
float* p_ty = Ty.ptr(i);
float* p_diff = diff.ptr(i);
for (int j = 0; j < S.cols; j++)
{
float alpha_diff = alpha_2 * p_diff[j] * p_diff[j];
float a1 = p_sx[j] * p_sx[j] + p_sy[j] * p_sy[j] + alpha_diff; //分母
float a2 = p_mx[j] * p_mx[j] + p_my[j] * p_my[j] + alpha_diff;
if (a1 > 0.00001 && a2 > 0.00001)
{
p_tx[j] = p_diff[j] * (p_sx[j] / a1 + p_mx[j] / a2);
p_ty[j] = p_diff[j] * (p_sy[j] / a1 + p_my[j] / a2);
}
}
}
} (6)计算相似度代码实现:
//获取黑色边缘的mask矩阵
void cal_mask(Mat Tx, Mat Ty, Mat &mask)
{
mask.create(Tx.size(), CV_8UC1);
for (int i = 0; i < Tx.rows; i++)
{
float *pTx = Tx.ptr(i);
float *pTy = Ty.ptr(i);
uchar *pm = mask.ptr(i);
for (int j = 0; j < Tx.cols; j++)
{
int x = (int)(j + pTx[j] + 0.5);
int y = (int)(i + pTy[j] + 0.5);
if (x < 0 || x >= Tx.cols || y < 0 || y >= Tx.rows)
{
pm[j] = 0;
}
else
{
pm[j] = 255;
}
}
}
}
//计算归一化互相关系数
double cal_cc_mask(Mat S1, Mat Si, Mat Mask)
{
double result;
double sum1 = 0.0;
double sum2 = 0.0;
double sum3 = 0.0;
for (int i = 0; i < S1.rows; i++)
{
for (int j = 0; j < S1.cols; j++)
{
if (Mask.ptr(i)[j])
{
sum1 += (double)(S1.at(i, j)*Si.at(i, j));
sum2 += (double)(S1.at(i, j)*S1.at(i, j));
sum3 += (double)(Si.at(i, j)*Si.at(i, j));
}
}
}
result = sum1 / sqrt(sum2*sum3); //范围0~1
return result;
} (7)微分同胚demons算法的最终实现:
void register_diffeomorphic_demons(Mat F0, Mat M0, float alpha, float sigma_fluid, float sigma_diffusion, int niter, Mat &Mp, Mat &sx, Mat &sy)
{
Mat F, M;
F0.convertTo(F, CV_32F); //将参考图像和浮动图像都转换为浮点型矩阵
M0.convertTo(M, CV_32F);
//初始化位移场为0位移
Mat vx = Mat::zeros(F.size(), CV_32FC1);
Mat vy = Mat::zeros(F.size(), CV_32FC1);
float e_min = -9999999999.9;
Mat sx_min, sy_min;
Mat Sx, Sy;
get_gradient(F, Sx, Sy); //计算参考图像梯度图
Mat M1 = M.clone();
for (int i = 0; i < niter; i++)
{
Mat ux, uy;
//计算Active demons的位移场
demons_update(F, M1, Sx, Sy, alpha, ux, uy);
imgaussian(ux, ux, sigma_fluid); //高斯滤波
imgaussian(uy, uy, sigma_fluid); //高斯滤波
vx = vx + ux; //将位移场累加
vy = vy + uy;
imgaussian(vx, vx, sigma_diffusion); //高斯滤波
imgaussian(vy, vy, sigma_diffusion); //高斯滤波
exp_field(vx, vy, sx, sy); //将累加的位移场转换为微分同胚映射
Mat mask;
cal_mask(sx, sy, mask); //计算黑色边缘的mask掩码矩阵
movepixels_2d2(M, M1, sx, sy, INTER_LINEAR); //对M像素重采样
float e = cal_cc_mask(F, M1, mask); //计算F、M1的相似度
if (e > e_min) //如果相似度提高,则更新最佳位移场
{
printf("i=%d, e=%f\n", i, e);
e_min = e;
sx_min = sx.clone();
sy_min = sy.clone();
}
}
sx = sx_min.clone(); //得到最优微分同胚映射
sy = sy_min.clone();
movepixels_2d2(M, Mp, sx, sy, INTER_LINEAR);
Mp.convertTo(Mp, CV_8U);
}07 测试结果
为了验证我们实现的微分同胚算法对大形变图像的配准效果,我们分别使用本文实现的微分同胚demons算法、Active demons算法对以下大形变的心脏图像进行配准,并比较结果:
由前文可知,Active demons算法中的alpha参数越大,配准步长越小,反之则配准步长越大。由于是大形变图像,我们统一给alpha取一个较小值0.15,高斯滤波参数sigma_fluid和sigma_diffusion都取0.05,迭代次数设置为3000。配准结果如下:
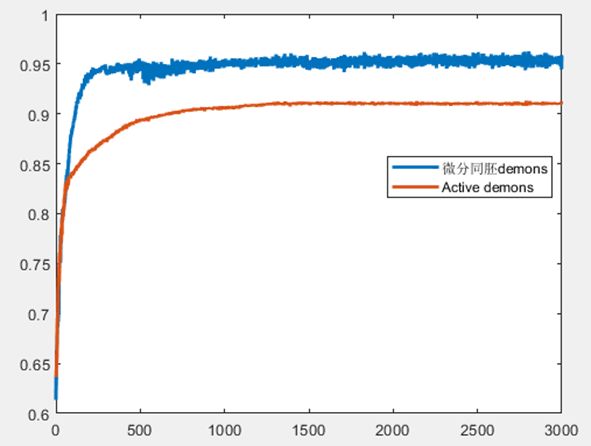
记录每轮迭代的配准图像与参考图像的相似度,如下图:
由以上结果可知,微分同胚demons算法的配准结果比Active demons算法的好得多。Active demons算法不适用于大位移,那么我们尝试把alpha调大为1.15,使位移减小,得到Active demons算法的以下结果,发现还是不理想。
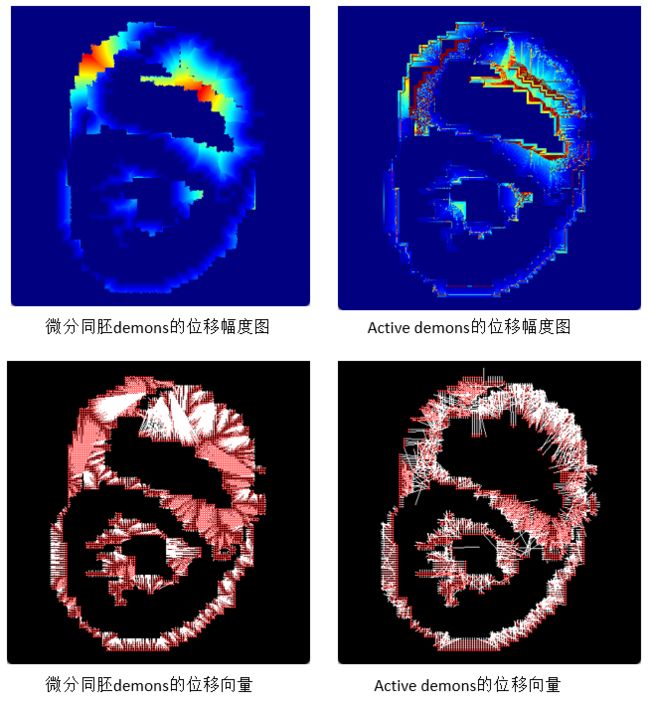
上文我们讲到,微分同胚映射是一种光滑的映射,什么是光滑映射呢?现在我们分别计算微分同胚demons算法、Active demons算法的最终位移场的位移幅度图(也即计算每个像素点的位移距离)并作伪彩色处理,同时画出每一个像素点的位移向量(白色线为位移轨迹,红点为位移终点),如下图所示,可以形象地看出来微分同胚映射的位移场是光滑的,相比Active demons算法的位移场就粗糙多了。
本文参考文献:
[1] Vercauteren T , Pennec X , Perchant A , et al. Diffeomorphic demons: efficient non-parametric image registration.[J]. NeuroImage, 2009, 45( 1):S61-S72.
微信公众号如下,会不定期更新精彩内容,欢迎关注: