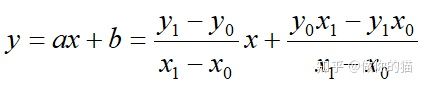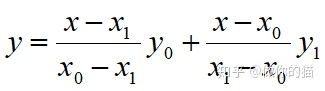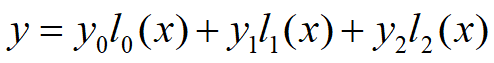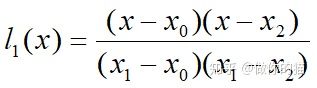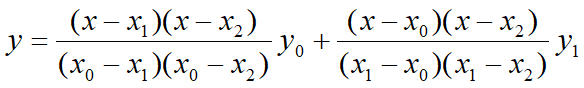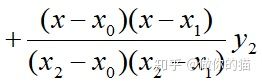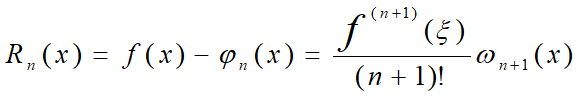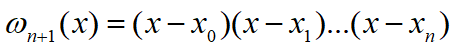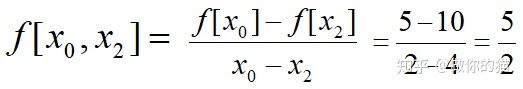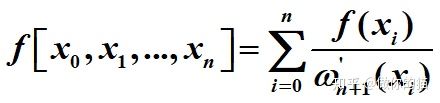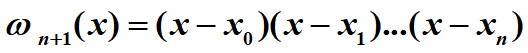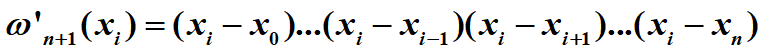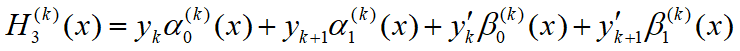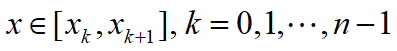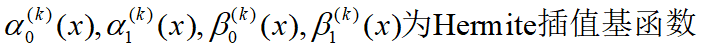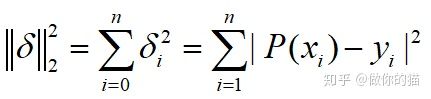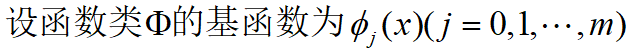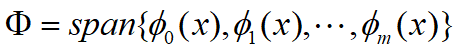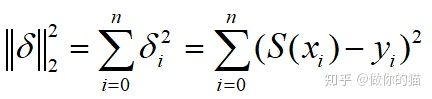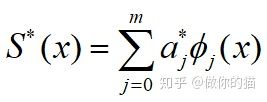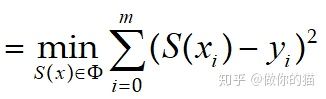matlab做三次拉格朗日插值多项式_计算方法/数值分析 ——第四章函数插值与曲线拟合...
一、函数插值:
1、插值,一类函数近似问题。
构造某个函数作为不便于处理或计算的函数的近似,然后通过处理简单函数获得不便处理或计算的函数的近似结果,当要求近似函数取给定的离散数据时,这种处理方法称为插值法。
插值的任务就是由已知的观测点,为物理量(未知量)建立一个简单的、连续的解析模型,以便能根据该模型推测该物理量在非观测点处的特性。
2、由于插值函数p(x)的选择不同,就产生不同类型的插值。
——若p(x)为代数多项式就称为代数插值
——若p(x)为三角多项式就称为三角多项式插值
——若p(x)为有理函数就称为有理函数插值
选择不同的插值函数,近似的效果不同。
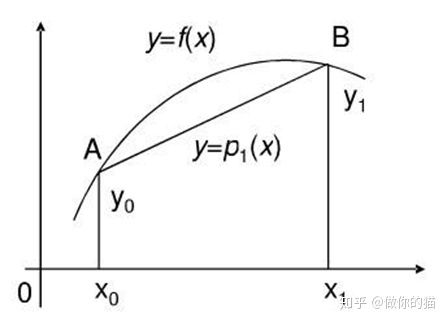
3、线性插值
n =1
求一次多项式:P1(x)=ax+b;用直线近似地代替函数f(x),则称这种插值为线性插值。
p1(x)满足条件:P1(x0)=y0 , P1(x1)=y1
可以解得直线的方程为:
可以写为:
其中令
l0(x)和l1(x)具有的特点:
l0(x0)=1, l0(x1)=0;
l1(x0)=0, l1(x1)=1;
l0(x), l1(x)称为以x0 , x1为节点的插值基函数。
4、线性插值仅仅用两个节点上的信息,精度较低。为了提高精确度,考察三点的插值问题。——二次插值
二次多项式 p2(x)=a0 + a1x + a2x2
使其满足条件: p2(x0)=y0, p2(x1)=y1, p2(x2)=y2;
解一个三元一次线性方程组即可解得系数a0, a1, a2,即可以得到二次多项式的表达式。
也可以表示成基函数的形式
其中
l0(x) , l1(x) , l2(x) 称为以x0 , x1 , x2为节点的插值基函数。
5、拉格朗日插值多项式
将n=1和n=2的线性插值和抛物插值推广到一般情况,即n次插值,也就是拉格朗日插值。
对于有n+1个插值点时,插值函数可以表达成一个n次多项式:
Pn(x)=a0 +a1x +a2x2 + …+ anxn ,
满足:
Pn(x0)=y0 , Pn(x1)=y1 , ... , Pn(xn)=yn
同样该n次多项式也可以表示为:
其中l0(x) , l1(x) , …,ln(x) 为以 x0, x1,…, xn为节点的插值基函数
拉格朗日插值函数:
6.插值余项
用插值多项式表示函数,则必然存在误差。
若在区间[a, b]上,用Ln(x)表示f(x),则其截断误差Rn(x)=f(x)-Ln(x),也称为插值多项式的余项
f(n+1)(x) 是f(x)的n+1阶导数在 x 的值。
7.牛顿插值法
差商定义:
一阶差商:
设有函数f (x)以及自变量的一系列互不相等的x0< x1<,…,< xn (即在i 不等于j时,x i不等于xj)的值 f(xi) , 称
为f (x)在点xi, xj处的一阶差商,并记作f [xi , xj] ;
二阶差商:
为f (x)在点xi, xj, xk处的二阶差商。
k阶差商:
为f (x)在点x0, x1,…, xk处的k阶差商。
0阶差商:
由差商定义可知:高阶差商是两个低一阶差商的差商
例题 :
差商性质:
(1)
(2)差商与节点排列顺序无关
8.牛顿插值多项式
f(x)= f[x0]+(x-x0) f[x0,x1]+(x-x0)(x-x1) f[x0,x1,x2]+…+(x-x0)…(x-xn-1) f[x0,…,xn]+(x-x0)…(x-xn-1)(x-xn)f[x,x0,…xn];
9.分段差值
两点三次Hermite插值多项式
二、曲线拟合
1.曲线拟合问题仍然是已知 x1 … xn; y1 … yn,求一个简单易算的近似函数 f(x)来拟合这些数据。
但是yi 本身是测量值,不准确
这时不能取 f(xi) = yi , 而要使 pi=f(xi) - yi 总体上尽可能地小。
这种构造近似函数 的方法称为曲线拟合,f(x) 称为拟合函数。
使 pi=P(xi) - yi 尽可能地小”有不同的准则
但
最小二乘法的基本概念
定义平方误差: