人脑网络在连接体特有的谐波中发挥作用（2015）

Selen Atasoy1, Isaac Donnelly2 & Joel Pearson1

1 School of Psychology, University of New South Wales, Sydney, New South Wales 2052, Australia. 2 School of Mathematics and Statistics, University of
New South Wales, Sydney, New South Wales 2052, Australia. Correspondence and requests for materials should be addressed to S.A. (email:
[email protected]).        

目录

摘要

引言

结果

讨论

方法

---

摘要

        人类大脑活动的一个关键特征是形成依赖于行为的大脑网络的连贯的、空间分布的振荡。然而，这些网络背后的一个基本原则仍然未知。在这里，我们报告说，人类大脑的功能网络是由谐波模式预测的，在整个自然界中无处不在，由人类大脑皮层的解剖学指导。我们介绍了一种将傅立叶基扩展到人类连接体的新技术。在这种新的特定频率的皮质活动表示中，我们称之为“连接体谐波”，人类大脑在静止状态下的振荡网络与某些频率的谐波模式相匹配。我们用连接体上兴奋-抑制相互作用的连续神经场模型证明了连接体谐波自组织背后的神经机制。值得注意的是，神经场模式和微妙的兴奋-抑制平衡之间的关键关系符合在意识丧失和恢复期间观察到的神经生理学变化。

引言

        自然过程的基本原理是由物理定律表示的，即测量的性质之间的定量关系，这些关系总是真实的1。尽管神经元兴奋机制的发现为解释单个神经元的行为提供了一个里程碑2，但集体神经动力学的一个基本原理在很大程度上仍然难以捉摸。

        哺乳动物大脑皮质动力学的一个特征是在频域中出现了跨越五个数量级的行为相关的振荡网络。最近，用功能磁共振成像(FMRI)测量的血氧水平依赖信号的自发缓慢(o0.1赫兹)波动也发现了广泛分布的皮质区域内的强时间相关性。这一发现表明，在没有任何外部刺激或任务条件的情况下，自发活动在整个大脑中也表现出高度结构化的关联模式。值得注意的是，这些被称为静息状态网络(RSNs)56的相关模式的地形图非常类似于由各种感觉、运动和认知范式识别的人类大脑的功能网络67，并且已被发现与脑电微态有关，即发生在大约100毫秒的离散周期中的全局大脑状态(参考文献89)

        RSNs被认为是由局部皮质动力学和皮质-皮质相互作用产生的，受人类皮质的解剖结构限制--人类的连接10，11。事实上，各种计算模型已经从解剖连接、局部皮质动力学和皮质-皮质相互作用探索了这种振荡网络的自发出现10，12。然而，我们对神经活动的理解缺乏一个统一的基本原理，揭示了集体皮质动力学的直接宏观描述3。

图1|拉普拉斯本征函数和连接体谐波。(A)拉普拉斯本征函数揭示矩形金属板(第1排)--由Ernst Chladni首次展示由沙子在振动金属板上形成的图案--和哺乳动物皮肤形状的金属板(第2排)在不同频率振动下类似于不同哺乳动物的毛皮图案的机械振动21、22(经允许转载自22)以及用与时间无关的薛定谔波函数计算的氢原子电子轨道--从左至右显示能量不断增加--以及激光激发离子晶体之间出现电磁相互作用的图案(最后一排)(图片改编自15)。(B)建造大尺度连接体模型的工作流程。图形表示是通过将从皮质表面采样的每个节点与其直接局部相邻节点连接起来，并进一步包括皮质和丘脑皮质纤维的端点之间的远程连接来形成的。(C)20个最低频率连接器谐波的例子。左图：波形号。右图：由连通体拉普拉斯特征向量估计的同步振荡的空间模式

        在这里，我们证明了一个无处不在的数学框架，即拉普拉斯算子的特征分解，它位于热、光、声、电、磁、引力和流体力学理论的核心13，可以在宏观尺度上预测人类皮质活动的集体动力学。在各种自然现象中，拉普拉斯的本征函数构成了系统中自组织图案的基础：吉他弦或金属板的声音诱导振动中出现的驻波图案(首先由Chladni14证明为复杂的沙图案)，从电磁相互作用中出现的离子运动图案15，16，由与时间无关的薛定谔方程17，18给出的自由粒子的电子波函数，以及在复杂动力系统中出现的甚至图案，例如Turing19引入的反应-扩散模型，它可以解释生物图案形成的各种情况，通过拉普拉斯算子21，22(图1a)的本征函数来预测。此外，在具有周期边界条件(如圆)的一维区域上计算的拉普拉斯特征函数对应于众所周知的傅立叶基础23。该关系已被用来将傅里叶变换扩展到更复杂的几何图形23，并在形状识别中定义‘Shape DNA’24

        我们研究了将拉普拉斯特征函数扩展到人类连接体的特殊结构，即连接体的谐波，作为宏观尺度皮层活动的新表示。值得注意的是，当在这部新的连接组特定的傅立叶基扩展，RSN匹配与某些自然频率(拉普拉斯特征值)相对应的空间模式(拉普拉斯特征函数)。我们的结果表明，拉普拉斯特征函数可以为静息状态下整个大脑皮层的同步模式提供一个简单但几乎通用的描述。此外，我们通过用神经场模型模拟兴奋性和抑制性动力学，论证了大脑皮层和丘脑大脑皮层相互作用中出现这些模式背后可能的生物学机制。

结果

        连接体谐波预测休眠状态网络。为了定义应用于人类连接体的拉普拉斯算子的扩展，我们利用了它的离散对应的图拉普拉斯算子。我们首先为10个人类连接创建了一个图形表示，方法是将从10个受试者的MRI数据中提取的皮质表面与从相同受试者的扩散张量成像(DTI)数据中得到的皮质纤维束生成的远程(白质)皮质和丘脑-皮质连接结合在一起(图1B)。对于每个受试者，我们形成了建模的连接体的图形表示G？V？；E，其中节点V？vi I 21；；n j f g，n是节点的总数-均匀地采样皮质表面和边缘的弯曲解剖E？EIj vi；Vj，2 VV包括局部和远程皮质-皮质和丘脑-皮质连接。通过计算引入的表示G上的图拉普拉斯DG，我们定义了应用于人类连通体的拉普拉斯算子的离散对，每个个体的连通体拉普拉斯算子，并估计了它的本征值-特征向量对ij；cj？，j2N，连通体调和(见方法)。值得注意的是，这里所说的谐波指的是空间谐波，而不是时间谐波。我们将在后面看到，这些空间谐波可以从神经元看似合理的动力学中出现，但在这个阶段，我们将拉普拉斯特征函数建立在静态结构连接上。同样值得注意的是，引入的图G不同于以前在人口模型10中使用的人类连接体的图形表示，因为它没有包括任何皮质表面以及皮质-皮质和丘脑-皮质连接的分割。因此，它提供了一个密集采样的连接体模型，在给定的MRI和DTI数据分辨率下具有最小的离散化量。值得注意的是，当从底层流形(例如大脑皮层表面)获取的均匀采样数据点的数量增加时，图形拉普拉斯收敛到其连续对应的拉普拉斯-贝尔特拉米算子-拉普拉斯-贝尔特拉米算子-拉普拉斯到非欧几里得几何的推广，例如人类大脑皮层的弯曲解剖25

        在文献中，拉普拉斯特征值-特征向量对(特征模)最初因为它们与给定几何形状的激发谱的关系而受到极大的关注：特征值与特定几何形状上出现的驻波的固有频率、允许频率有关，而特征向量产生相关的波型18、23。最近的研究还证明了拉普拉斯本征模与其他物理现象的相关性，包括电子波函数的相位提取18、离子15、16和形态发生22、26的电磁相互作用中出现的图案(图1A)。在这里，我们利用连接体拉普拉斯的特征向量来描述大尺度神经活动的时空模式。

        我们发现，连接体拉普拉斯函数的特征向量，即连接体谐波，在分布的皮质区域产生特定于频率的空间模式(图1C；补充图1)。在这里，红蓝图案代表了一个代表性受试者的前20个连接体谐波的例子，按照频率的升序(波数显示在左侧)。

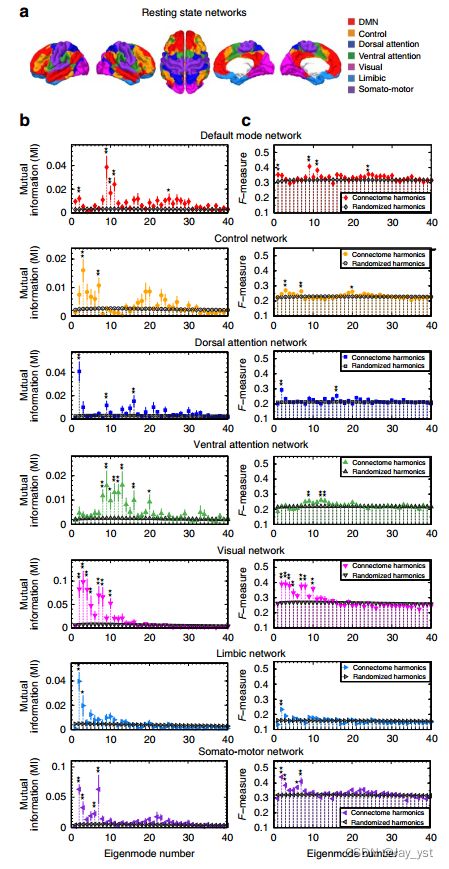
图2|通过连接体谐波预测RSNs。(A)人脑的同步振荡模式，即RSNs，与已建立的功能系统重叠，即在某些任务中共同激活的一组皮质区域6，7。为了定量评估RSNs与连接组谐波之间的任何相似性，我们使用了从1,000名受试者的固有功能连接性数据27中识别的七个RSNs(默认模式、控制、背部注意、腹侧注意、视觉、边缘和躯体-运动网络)(见a)。(B)用互信息衡量的相似性；(C)用F测量值衡量的40个最低频率的连接体谐波与参考RSNs之间的预测能力。27(如a所示)与随机化的谐波相比(*Po0.0002，**Po0.0001由蒙特卡罗模拟估计，每个受试者2,000个模拟和群体平均500,000个模拟，在通过错误发现率进行多次比较校正后，误差条指示10个受试者的标准误差)。

        为了定量评估连接体谐波与人脑中常见的七个RSN(图2a)之间的相似性；默认模式、控制、背部注意、腹侧注意、视觉、边缘和躯体-运动网络，我们测量了参考RSN27与每个连接体谐波模式之间的互信息(图2B：填充的彩色数据点)。作为对照，我们进行了蒙特卡罗模拟(每个受试者随机结合2,000个模拟与组平均500,000个模拟)，其中我们随机化了远程白质-皮质和丘脑-皮质连接，同时保留了受试者皮质表面的局部解剖结构，并使用相同的方法计算了每个随机网络的谐波(图2B：黑色数据点)。至关重要的是，我们在组平均(图2B，顶行，*Po0.0002，**Po0.0001；组平均的500,000蒙特卡罗模拟，修正了多次比较)以及所有10个受试者的个体(补充图)中发现了默认模式网络(DMN)和一个特定的连接体谐波(在第9个连接体谐波的范围内，由于个体差异)之间的统计上显著的相似性。P值：*Po0.05，**Po0.02；每个受试者2,000个蒙特卡罗模拟，经多次比较校正)。对于所有其他静止态网络，我们观察到互信息值的个体差异较大(补充图2和3)，而蒙特卡罗模拟在群分析中仍然对不同范围的连接体谐波产生显著的相似性(图2B)。特别是，我们发现视觉、躯体-运动和边缘网络仅与低频连接体谐波有显著的相似性，而与较高认知功能相关的网络，即控制、背部注意和腹侧注意，与空间频谱上分布的广泛的连接体谐波显著匹配。

        为了进一步评估连接体谐波对静止态网络的预测能力，我们使用了一个信息检索度量F-MEASURE，它同时量化了连接体谐波对RSN的预测的召回率和精确度。我们计算了连接体谐波(在应用二进制指示函数后)和RSN27的二进制模式之间的F-测量值，并将其与蒙特卡罗模拟得到的随机谐波的F-测量值进行了比较。F-度量提供了比信息论互信息更严格的评估，因为指标函数对每个节点施加了二元判决。这项评估(图2C；补充图4和5)证实了我们之前基于相互信息的发现。综上所述，这些结果表明，视觉、躯体运动和边缘网络以及默认模式网络都可以通过窄频率范围的个体连接体谐波来很好地预测，而较高的认知网络依赖于分布在空间频谱上的更宽频率范围的连接体谐波。

        作为连通体上傅立叶基函数的连通体。接下来，我们研究了使用连接体谐波作为函数基础来表示大脑皮层网络的空间模式。连接体谐波的正交性意味着这些特征函数的线性组合可以用来重建神经活动的任何空间模式。连通体谐波基的重要性与经典傅里叶变换关系密切，对应于将信号分解为应用于圆域的拉普拉斯算子的特征函数的线性组合，即具有不同频率的正弦和余弦函数23。由于连接体的谐波被定义为连接体的特征向量拉普拉斯--应用于人类连接体的拉普拉斯的离散对应--它们将傅立叶基扩展到人类连接体的特定几何形状。因此，到连接体谐波的谱变换自然地将经典的傅里叶变换扩展到人类连接体。         

 图3|基于连接体谐波基的RSNs重建。与随机二进制模式的重建相比，使用(A)0.1%和(B)1.2%的跨10个对象的平均连接组谐波谱(误差条和阴影表示跨10个对象的标准误差)的每个静止状态网络的归一化重建误差。A中的红色带突出了DMN的最大降幅。(C)使用(从上到下)5%、0.5%和0.05%的频谱和一个受试者数据的最佳匹配连接体谐波重建DMN。

        为了分析静息状态网络27(图2a)的空间频率内容，我们对连接体谐波基进行了频谱变换，并重建了单个网络的空间模式。尽管参考网络的二进制性质在理论上需要使用整个连接体谐波谱进行重建--就像方波只能使用具有无限多个频率的正弦波进行重建一样--但仅使用0.1%的连接体谐波谱(低频范围；图3A)就可以观察到归一化重建误差的急剧减少。DMN重建误差的最急剧下降发生在频段，该频段分别在互信息和F测量值方面也显示出显著的相似性和预测力(由图3A中的红柱突出显示，每个受试者的最佳匹配连接体谐波如图6所示，重建如图3C所示)，而对于视觉、躯体-运动和边缘网络，重建误差的下降幅度仍然很大，但在频谱的0.1%内保持不变(图3A)。在1.2%的频谱范围(低频范围)内，观察到较高认知网络的重建误差收敛较慢，这表明这些网络对更广泛的频率范围的依赖(图3B)。这些结果证实了我们之前的发现，同时提供了一种类似于经典傅立叶变换的皮质活动的新分析语言，可以用来量化任何活动模式，包括基于任务的事件相关设计。

        连接体谐波的生物学机制。我们还研究了大脑皮层连接体谐波自组织的生物学机制。到目前为止，我们一直假设基于结构连通性的图拉普拉斯提供了有效连通性的可信代理(也称为雅可比-请参见参考文献)。28)潜在的神经动力系统。在接下来的内容中，我们将探索这些神经动力学可能的生物学机制。特别是，我们利用神经场方程在连接体谐波方面对这些动力学的有效描述，并展示它们如何引起皮层上连接体谐波的出现。

        振荡的皮质网络的动力学被认为是由兴奋和抑制的相互作用产生的；例如，谷氨酸能主细胞和抑制；例如，介导的g-氨基丁酸GABA能神经元间。为了描述大脑皮层动力学，我们扩展了一种基于威尔逊-考恩方程的神经场模型，威尔逊-考恩方程是兴奋-抑制神经动力学最常用的数学描述30。基于威尔逊-考恩方程的神经场模型是反应扩散系统31的一种变体，最初由图灵作为形态发生的数学模型19引入。基于扩散激活剂和抑制剂之间的相互作用可以导致自组织图案形成的原理，反应-扩散模型为非线性波在几个生物过程中出现的机制提供了有价值的见解，这些生物过程包括形态发生19、20、视觉皮质中眼睛优势模式的形成32、视觉幻觉33、34以及皮层和丘脑组织神经群中兴奋和抑制活性的相互作用。重要的是，反应扩散系统中的图案形成是由应用于图案化域的拉普拉斯函数的某些特征函数的指数增长引起的(见参考文献21、22和补充注释1-4)。选择哪些谐波模式被“激活”(增长)取决于激励和抑制的扩散参数(补充图7)。因此，拉普拉斯本征函数为反应扩散系统中出现的复杂模式提供了基础。

        在大脑皮层的二维连续理想化上，当短程刺激与更广泛的侧向抑制相结合时，威尔逊-考恩方程导致神经振荡模式的自组织36。这种被称为“墨西哥帽”组织的功能回路，或中心开启和环绕关闭的连接，在早期的视觉皮质中得到了很好的实验观察，被称为皮质环绕抑制39，40，并且很可能延伸到整个新皮质41，42。

        最近的实验证据表明，V1中皮层环绕抑制的一个可能的机制是小鼠视觉皮质浅层中表达生长抑素的抑制神经元的活动，而在其他皮质区域42中也可能存在类似的神经回路。与兴奋相比，清醒小鼠初级视皮层中抑制的空间范围更广，这进一步支持了这些发现。此外，层特定的抑制和促进也为侧向抑制相互作用产生必要的回路29，44：浅层(L2/3)和深层皮层(L5)的协调调制引起相邻区域之间的竞争和侧向抑制，尽管跨皮质区域的兴奋和抑制的空间程度在垂直(跨皮质层)和水平(层内)上呈现重叠分布44。值得注意的是，已经证明，当总兴奋电导的一部分慢于抑制时，也可以在具有短程抑制的解剖电路中产生墨西哥HAT类型的功能电路37。兴奋性传导减慢的一个潜在生物来源是N-甲基-D-天冬氨酸受体引起的突触传递减慢，对兴奋性电流起主要作用。

        综上所述，这些聚合证据表明，不同的生物机制可以产生相当于短程兴奋和广泛抑制的功能电路，这确实是Wilson-Cowan型神经场模型30、33、35(补充注释1-5)中振荡模式自组织的必要条件。接下来，我们通过引入连接体拉普拉斯方程将Wilson-Cowan方程扩展到丘脑-皮质系统的完全结构连通性，并演示了新出现的振荡模式和连接体谐波之间的关系

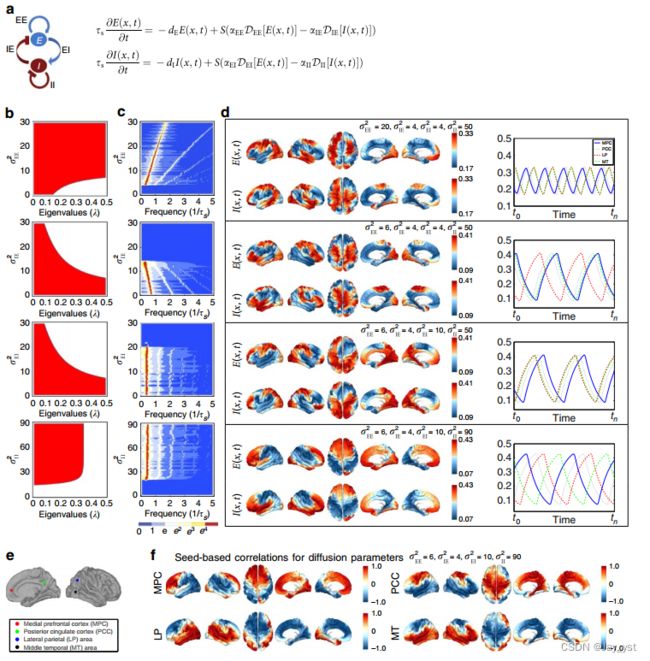
 图4|神经场模型。(A)左：兴奋性(E)和抑制性(I)活动的动力学。右图：皮层位置vi 2V的兴奋性E(vi，t)和抑制性I(vi，t)活动在时间t的时间演化，其中dee、die、dei和dii描述E和I活动在兴奋性(EE，IE)和抑制性(EI，II)神经种群上的扩散过程，ts是指系统时间的单位，即特征时间尺度。(B)神经场模型关于连接体谐波的线性稳定性分析。红色区域对应于在代数上满足振荡必要条件的相空间中的扩散参数，即临界Hopf区域，绘制为所分析的扩散参数垂直轴和连接体简谐水平轴的本征值的函数。(C)所有节点平均的(总共267次)数值模拟中的时间振荡的功率谱。(D)任意时间片的空间模式和四个种子位置的时间轮廓，见E.(F)基于种子的神经场模式的相关分析表明，对于同一组参数，DMN的中线后和前中线节点之间的去耦合导致了缓慢的皮质振荡

        全连接神经动力学的神经场模型。通过将连接体拉普拉斯纳入空间传播(扩散)项，我们将基于Wilson-Cowan方程30的神经场模型35的变体扩展到三维连接体模型(图4A；补充说明2和3)。然后，通过将人体连接体上的网络扩散与兴奋-抑制反应动力学(图4A)相结合进行数值模拟-通过迭代应用对称图Laplacian23，45DG来建模。这允许我们通过结合人类连接体的连接性来扩展连续形式的神经场模型。这种神经场方法不同于以前的宏观尺度模拟10，46因为空间传播是通过网络扩散而不是离散耦合来建模的，从而产生了(空间上)近连续的皮质动力学模型。

       我们发现，在模型中，对于广泛的扩散参数，结构化的振荡模式在人类连接体上自然地自组织(图4a-d；补充图8和9；补充电影1-4)。对神经场模型的线性稳定性分析表明，在不同的激励和抑制扩散速度下，可以激活大范围的连接体谐波(图4B；补充注释3-5)，使神经场模型成为连接体谐波自组织的一种可信的神经机制。特别是，我们观察到，当兴奋活性降低时，以较慢的兴奋扩散为模型，或当抑制活性增加时，相干振荡的频率降低，以神经场模型中抑制的较快扩散为模型(图4C，d)。时间振荡的频率和兴奋-抑制平衡之间的关系表明与在意识丧失和恢复期间观察到的神经生理变化显著重叠(就所分析的参数范围而言)。神经生理学证据表明，药物或睡眠导致的意识丧失与增加的抑制或减少的兴奋活动有关，这伴随着皮层活动从低幅度、高频模式向低频相干振荡的转变47。最近的研究还表明，在失去意识的过程中，DMN的中线后部和前部中线节点之间逐渐脱钩48，49。我们在基于种子的神经场模式的准确参数相关分析中观察到了这种去耦合，这导致了较慢的皮质振荡(图4e，f；补充图9)。

图5|神经场模型的稳定性分析。通过扰动样本振荡参数集的神经场模型来测试新出现的振荡对外部扰动的稳定性(S2 EE？6、S2 IE？10、S2？Ei？10和S2？II？50)。(A)距离度量L(T)与从扰动开始的时间t，t*的关系，其中t*表示白噪声扰动的时间。在微扰之前，L(T)等于0。L(0)表示受扰动的系统与基础振荡稳定状态的变化程度。摄动后，即当t，t*40，L(T)趋于0时，系统是Lyapunov稳定的。(B)极限环的收敛；即，摄动(黑色实线)到未摄动(橙色虚线)系统的两个不相邻节点的兴奋活动随时间的变化。(C)摄动t，t*A[0，5]单位时间后两个样本顶点(绿线和蓝线)的原始(未扰动)轨迹(虚线)和扰动轨迹(实线)。摄动轨迹收敛到原始轨迹(有小的相移)，表明对应于原始轨迹的状态对小扰动是稳定的。

        最后，我们使用Lyapunov稳定性分析50测试了新出现的振荡模式对外部扰动(如噪声)的稳定性。这种方法涉及在某个时刻t*扰动系统，并观察扰动系统是否收敛到原始系统。在动力系统中，如由神经场模型描述的，线性化系统在已知固定点附近的特征值立即揭示系统的局部行为；也就是说，它将使人们能够识别主导观察到的波动的不稳定的“增长”特征模(补充说明3-5)。然而，由于威尔逊-考恩方程固有的非线性以及建模系统的高维性，不动点的连续体，即轨迹，并不容易获得。因此，我们对系统进行数值积分，以确定某些参数的稳定解，在我们的例子中是周期解。我们首先在时间t*分别用白噪声扰动系统10次，并通过计算L-无穷大范数L(T)来分析未被扰动的轨迹和每个扰动轨迹随时间的最大差异(见方法)。图5a显示L(T)是有界的并且收敛到eE0，而图5b，c说明了对于两个示例顶点v1和v2，扰动系统的极限环和时间振荡与未扰动系统的极限环和时间振荡的收敛。这些结果表明，在所分析的参数范围内，扩展的Wilson-Cowan方程(图4A)对外部扰动(如噪声)是稳健的。

        综上所述，将Wilson-Cowan类型的神经场模型扩展到人类连接体的特殊结构连接性提供了一种生物学上可信的、健壮的机制，可能是丘脑-皮质系统中连接体谐波自组织的基础。

讨论

        我们的结果揭示了几个值得注意的发现：首先，通过将一个通用的数学框架，即拉普拉斯的特征分解，扩展到人类连接体的解剖结构，我们引入了连接体谐和--一个特定于连接体的傅立叶基的扩展--作为一种新的表示来描述和分析任何皮层活动的时空模式。值得注意的是，将RSN分解为连接体谐波，显示了静息状态网络和某些连接体谐波谱之间的显著重叠。这表明，连接体谐波提供了一种简单的解释原理，将振荡皮质网络的动力学与人类连接体的解剖学联系起来。这一发现是第一个实验证据，证明了无处不在的数学框架，即拉普拉斯的特征分解，当应用于人类连接体时，可以提供一个简单但几乎通用的原理，可能是大脑功能网络的基础。

        其次，由于对应于不同频率(波数)的连接体谐波的正交性，因此，所有连接体谐波的集合提供了一个函数基础(一种新的坐标系或表示法)来描述和分析任何皮层活动的时空模式，而与成像模式、实验设计甚至物种无关。虽然在这项工作中我们展示了这项新技术在人类连接组中的应用，但它可以扩展到任何其他哺乳动物的大脑，因为它的结构连接。因此，连接组谐波提供了一种新的特定频率的语言来描述神经活动的时空模式，并为探索不同物种和技术的大脑动力学的新维度打开了大门。

        具有有效的基集(连接体谐波)的潜在重要性可能与动态因果模型特别相关。实际上，在电磁活动的动态因果模型51中，拉普拉斯图的特征函数被用来总结皮质斑块的活动。从静息状态fMRI的动态因果模型的观点来看，功能连通性的特征模式被用作有效连通性的先验约束。我们的工作表明，这些可以用结构连接体的图拉普拉斯的本征函数来代替。此外，人们可以使用贝叶斯模型比较来判断基于结构和功能连通性的本征模式的效用--这将影响对我们的通用基集的进一步验证

        第三，在描述耦合动力系统时，我们强调了图的本征函数或本征模的普适性，如神经场模型。通过使用定义在人类连接体上的拉普拉斯图，我们演示了如何将经过充分研究的神经场模型(例如基于威尔逊-考恩方程30的那些模型)扩展到丘脑-皮质系统的完全结构连接性，并与人脑的RSN相关联。然而，由于连接体谐波的定义与所选择的动力学模型无关，无论是在解析上还是在数值上，所介绍的连接体谐波基的数学框架也可以应用于扩展其他更复杂的网络模型；(例如，参考文献10，12，52)，以(空间)近连续域中丘脑皮质系统的完全结构连通性。

        事实上，最近的计算模型表明，在静息状态下可以出现非常丰富和复杂的动力学，其特征是相关活动的几个离散状态之间可以出现快速转换52，这是由对相关状态的曲目的噪声驱动的探索启动的。这些计算研究得到了最近的经验证据的支持，这些证据表明不同RSN之间的复杂动力学。结合脑磁图数据的高时间分辨率和特定带宽的相关分析的研究表明，RSN随着时间的推移组装和拆卸，不仅能够在不同的网络内而且在不同的网络之间进行通信(通过相干振荡的周期)53-55。此外，fMRI研究使用滑动时间窗相关性而不是整个时间过程中的平均相关性，发现一组离散的连接状态，即相关神经活动的主要循环模式，在几十秒内出现并消失。。连接组谐和基可提供一种新颖的理论框架，用于将这些最新的经验发现与专注于噪声驱动的连接状态探索的高级计算模型联系起来，因为它们揭示了丘脑-皮质系统上的关联模式，并定义了一组独立的连接状态或构件，通过它们可以以非参数的方式表达复杂的动力学，例如，无需调整用于关联分析的时间窗口的大小58，59。因此，重新制定动力学模型，如文献[1]中的模型。52，在连接体方面，谐波可以揭示噪声驱动的过渡是如何在不同频率之间发生的，并导致不同RSN之间的通信。

        在大规模脑动力学的背景下，直观地理解连接组谐和在描述耦合动力系统中的作用，依赖于将图拉普拉斯与皮质节点之间的有效连接联系起来。换句话说，如果图的拉普拉斯对应于有效连接强度的矩阵，则其本征函数成为函数连通的本征模式或主分量。此外，拉普拉斯图或有效连通性成为观察到的活动波动的(负)偏相关矩阵28。这一点很重要，因为它解释了为什么基于图的拉普拉斯本征模提供了一个合理的空间来描述基于功能连通性的RSN。这种对应关系依赖于无向连通性(由对称邻接表示)矩阵，这意味着人们可以将有效连通性解释为调节神经元活动的‘扩散’。要完成此图，请注意图的对角项拉普拉斯确保到任何节点的输入连接之和为零(请参阅方法)。然而，值得注意的是，与其他物理现象中的扩散过程不同，神经活动不仅在局部传播，而且还通过长距离的白质丘脑-皮质连接传播，这一扩散过程发生在人类连接体的特定连接上。我们对拉普拉斯扩散图所隐含的普适调和的描述依赖于结构连接体的无向性质(由对称邻接矩阵表示)。然而，我们知道，相互的向前和向后连接在人脑中显示出强烈的不对称性，使得(定向的)有效连接和扩散之间的概念联系并不总是有效的。话虽如此，没有理由不能使用定向有效连通性矩阵的本征模式28进行建模和仿真。

        总之，在这项工作中，我们引入了一种新的连接特定的皮质活动模式和动力学表示，它将傅立叶基扩展到丘脑-皮质系统的结构连接。值得注意的是，当用这种新的分析语言表达时，人脑的RSN与某些频率的连接体谐波模式重叠。我们从神经场模型所描述的耦合动力系统中神经兴奋和抑制的相互作用中论证了这些连接特有的谐波模式的自组织。有趣的是，由于在各种自然现象中出现了这些谐波模式，从声振动、电磁相互作用、电子波功能到形态发生，人们很容易认为人类的大脑活动也可能受到与其他自然现象相同的潜在原理的支配。

方法

        

 数据。在准备这项工作中使用的数据是由人类连接组项目(HCP)、Wu-Minn联盟(主要调查人员：David Van Essen和Kamil Ugurbil；1U54MH091657)获得并提供的，该联盟由16个支持NIH神经科学研究蓝图的NIH研究所和中心以及华盛顿大学McDonnell系统神经科学中心资助。我们使用了10名无关受试者(6名女性，年龄22-35岁)的核磁共振和弥散张量成像数据，这些数据由HCP，Wu-Minn财团提供，可从https://db.humanconnectome.org/data/projects/HCP_500.获得。所有的MRI和DTI数据集都根据HCP协议的最低限度的预处理指南进行了预处理，并且没有进行额外的预处理。

        为了定量评估静息状态网络(RSN)，我们使用大脑皮质划分为七个网络(默认模式、控制、背侧注意、腹侧注意、视觉、边缘和躯体-运动网络)，这些网络来自1,000名受试者的内在功能连接数据27，可在http://surfer.nmr.mgh.harvard.edu/fswiki/CorticalParcellation_Yeo2011.上获得

工作流程。根据每个受试者的T1加权磁共振数据(分辨率0.7 mm)，我们使用Freesurfer软件http://freesurfer.net.分别为每个半球重建分隔白质和灰质的皮质表面，在手稿的其余部分称为白质表面，以及灰质和脑脊液，在手稿的其余部分称为灰质表面。我们将每个皮质表面配准到皮质分割数据的1,000个受试者的平均皮质面(在手稿的其余部分中称为平均受试者，由20,484个顶点表示)，以便允许在连接组谐波和静止状态网络的1,000个受试者平均参考之间进行顶点到顶点的比较。

        从每个受试者的DTI数据(分辨率为1.25 mm)中，我们通过使用斯坦福大学http://white.stanford.edu/newlm/index.php/MrDiffusion.的Vista Lab的MatLab实现应用确定性束成像算法60来提取白质皮质和丘脑皮质纤维。在记录了每个受试者的DTI数据和皮质表面后，我们在分隔白质和灰质的皮质表面上初始化用于纤维束成像的种子。以每个顶点(节点)为中心--总共20,484个--我们初始化8个种子，并使用以下参数执行光道成像：分数各向异性阈值0.3，即分数各向异性0.3是跟踪的终止标准，最小轨迹长度20 mm，以及两个连续跟踪步骤30之间的最大角度。

 人类连接体的图形表示。人类连接体G的图形表示是通过以下方式形成的：用节点V？vi i 21；；n j f g表示从灰质表面采样的顶点，其中n是节点总数(在本研究中为20,484个)，并通过将顶点之间的局部和远程连接包括为图的边E？Eij vi；Vj，2Vv形成。因此，局部连接对应于皮质表面网格上的顶点的连接(每个顶点六个连接到它们最近的邻居)，而远距离连接由白质皮质和丘脑皮质纤维决定。为此，在灰质皮质表面上识别每个纤维终点的最近顶点，并且为每个纤维束添加两个顶点之间的远距离连接。在本研究中，我们使用无向、未加权的图表示法来表示以下邻接矩阵：

值得注意的是，这个人类连接体的图形模型不同于以前的研究10，12，其中每个节点代表由大脑皮层的某一部分获得的一个皮质区域，边缘表示皮质区域之间的纤维密度。与以前的人类连接组的图形模型相比，我们研究中使用的特殊表示非常接近人类皮质的连续形式，因为从连续的灰质皮质表面均匀而密集地采样了顶点(节点)。

连接组拉普拉斯和连接组谐波。给定人类连接体的图形表示G？V？；E，我们计算连通体上的对称图拉普拉斯DG，以便估计应用于人类连接体的拉普拉斯算符23，45D的离散对应物，即连接体拉普拉斯：

   

表示图的度矩阵。然后我们计算连接组谐波;

        

李雅普诺夫稳定性。我们使用Lyapunov稳定性分析50来测试神经场模型对扰动的稳健性。这种方法涉及在某个时刻t*扰动系统，并观察扰动系统是否收敛到原始系统。如果是这样的话，这个系统可以称为李亚普诺夫稳定。

由于神经场模型对于我们关心的参数集是振荡的，所以我们必须定义一个度量，它确定两个状态之间的距离。

我们首先在时间t*用白噪声分别对系统进行10次扰动。然后，我们取每个时间步上每个节点的差值的绝对值，并取最大差值。这被称为L-无穷大范数，通常用于稳定性分析，因为它着眼于最坏的情况而不是平均的情况。在每个时间步，我们比较10个扰动系统的所有差异，并再次选择最坏的情况。这个量被定义为L(T)。我们绘制随时间变化的距离度量L(T)，并观察L(T)-0或L(T)-e与e0的关系。在图5(A)中，我们看到L(T)-e是有界的，证明了神经场模型对噪声扰动的稳健性

启发

       1. 探索图拉普拉斯谐波与七个不同静息态网络的相关性；

       2. 使用图拉普拉斯谐波的特征函数的线性组合表示大脑不同的空间模式（也就是图滤波），也是对七个不同静息态网络进行重建误差分析；