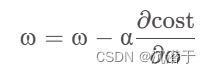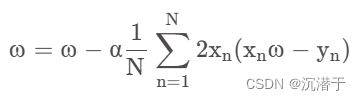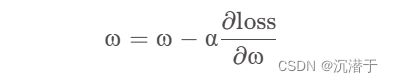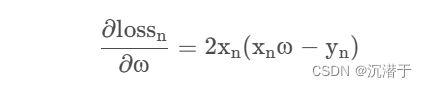【Pytorch学习笔记】003--梯度下降算法
1.引入
由【Pytorch学习笔记】002—线性模型。在简化目标函数为不含常数项的线性方程后,我们需要在w-cost曲线图中寻找一个最优的w值使得cost最小。但是当目标函数存在两个变量w、b,即含有常数项的线性方程,我们就需要在曲面中寻找一个使得cost最小的一个点。并且当多维(即多个参数)的情况下会引起维度诅咒问题。导致问题不可解,因此我们需要对该类问题进行改进。
穷举法:设定未知参数在一个范围内,如何逐一对这个范围的参数进行穷举
分治法:将大范围逐步通过一系列方法缩小范围,先对整体进行分割采样,在相对最低点进行进一步采样,直到其步长与误差符合条件
2.梯度下降算法
1.梯度:可以理解为导数
2.梯度下降算法核心公式(进行梯度的更新):
其中a表示学习率,不宜取得过大
3.梯度下降公式核心算法(带入化简):
4.梯度下降的局限性:
a.梯度下降算法能够保证找到的是局部最优点而不是全局最优点,但是实际问题中的局部最优点较少,或已经基本可以当成全局最优点
b.梯度下降算法极有可能陷入鞍点,导致权重无法进行迭代,这是我们需要解决的问题
5.梯度下降算法程序代码及示意图:
import matplotlib.pyplot as plt
import numpy as np
x_data=[1.0,2.0,3.0]
y_data=[2.0,4.0,6.0]
_cost=[]
w=1.0
def forward(x):
return x*w
def cost(xs,ys):
cost=0
for x,y in zip(xs,ys):
y_pred=forward(x)
cost+=(y_pred-y)**2
return cost/len(xs)
def gradient(xs,ys):
grad=0
for x,y in zip(xs,ys):
grad+=2*x*(x*w-y)
return grad/len(xs)
for epoch in range(300):
cost_val=cost(x_data,y_data)
_cost.append(cost_val)
grad_val=gradient(x_data,y_data)
w-=0.01*grad_val
print('Epoch:',epoch,'w=',w,'loss=',cost_val)
print('Predict(after training)',4,forward(4))
plt.plot(range(300),_cost)
plt.xlabel('Epoch')
plt.ylabel('Cost')
plt.show()
3.随机梯度下降算法
1.引入
随机梯度算法是在梯度算法上的改进,主要是为解决梯度算法存在的两点局限性。梯度下降算法针对整个数据集的损失,对权重w求偏导,进行权重的迭代。随机梯度算法针对单个样本的损失,对权重w求偏导,进行权重w的迭代,有可能利用单个样本的随机噪声来跳过鞍点,进行找到全局最优点而不是局部最优点。
2.随机梯度下降算法核心公式(进行梯度更新):
3.随机梯度下降算法核心公式(带入化简):
4.梯度下降算法与随机梯度下降算法对比
梯度下降算法因其并行性而效率高,但其性能较低;随机梯度下降算法性能较好,但因其无法利用并行性导致时间复杂度高
5.随机梯度下降算法程序代码及示意图:
import matplotlib.pyplot as plt
import numpy as np
x_data=[1.0,2.0,3.0]
y_data=[2.0,4.0,6.0]
_cost=[]
w=1.0
#前馈计算
def forward(x):
return x*w
#求单个loss
def loss(x,y):
y_pred=forward(x)
return (y_pred-y)**2
#求梯度
def gradient(x,y):
return 2*x*(x*w-y)
for epoch in range(101):
for x,y in zip(x_data,y_data):
grad=gradient(x,y)
w-=0.01*grad
print('\tgrd',x,y,grad)
l=loss(x,y)
print('Epoch',epoch,'w=',w,'loss=',l)
print('Predict(after training)',4,forward(4))
4.批量随机梯度下降算法
1.引入
在进行梯度下降算法和随机梯度算法的比较中,针对出现的问题选择一种折中的方法。将若干个样本分为一组,记录一组的梯度用以代替随机梯度下降中的单个样本