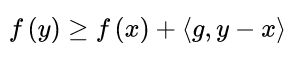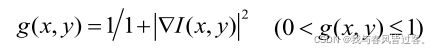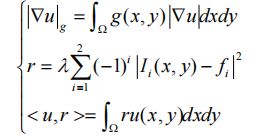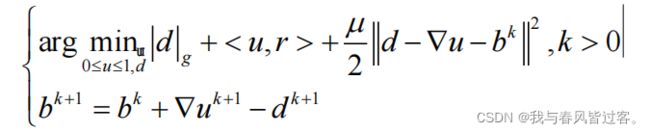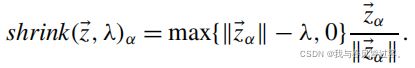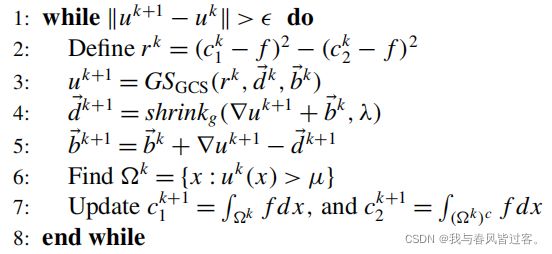基于水平集LBF模型的图像边缘轮廓分割凸优化 - Split Bregman分裂布雷格曼算法的最优解
目录
1. 凸优化简介 ：
2. 次梯度（subgradient）：
次梯度概念：
次梯度例子：
次梯度存在性：
3. Bregman距离(布雷格曼距离) ：
Bregman距离概念 ：
Bregman距离的含义 ：
介绍了一些准备知识，下面才开始正式的开始使用LBF模型的分裂布雷格曼迭代进行水平集分割轮廓.
4. LBF模型 ：
5. Split Bregman 凸优化：
算法（Algorithm）：
1. 凸优化简介 ：
凸优化，或叫做凸最优化，凸最小化，是数学最优化的一个子领域，研究定义于凸集中的凸函数最小化的问题。譬如在凸优化中局部最优值必定是全局最优值。凸函数的凸性使得凸分析中的有力工具在最优化问题中得以应用，如次梯度等。
为什么要引入凸函数并最优化呢？最主要的原因就是凸函数的最优解就是全局最优解。
2. 次梯度（subgradient）：
次梯度概念：
我们首先引入次梯度的概念，先来看一下次梯度的定义：
简单介绍一下，其中我们要找的次梯度就是 
，次梯度 是一个集合，该集合和自变量差的内积，小于等于两个自变量的函数值之差。
当 
时 ( 
表示 
的最优解 ，也就是 
时， 有极小值 )，原式子如下：
我们发现 
和 
的内积 
，内积大于等于 
，说明两向量的夹角 
°，所以当等式中的 
朝着次梯度 的反方向前进时，那么就有很大可能性靠近最优解 
，所以负梯度就是可导函数局部的最速下降点，那么再每个局部点都沿着负梯度搜索下去就能收敛到全局最优点。由次梯度的定义可知，次梯度也具备着类似的性质，只不过次梯度不依赖于可导的条件罢了.
需要注意的是函数在某点处的次梯度一般来说是一个集合，而并非一个点，这一点和梯度是有很大不同的，梯度一般是唯一的。我们用如下符号表示某点的次梯度：
只要满足次梯度那个定义的就是次梯度了，所有满足次梯度定义的构成了一个集合.
次梯度例子：
说到这里可能还是有点懵，初学者可能不太理解，那么举个例子说明一下。
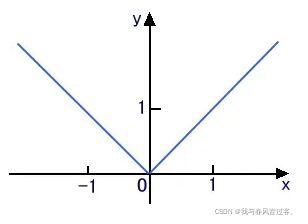
我们都了解的 L1范数，L1范数的一维形式，也就是绝对值函数 : 
，来了解一下此函数的次梯度是个什么情况.
了解过凸优化的大佬应该都知道支撑超平面的概念，我也是初学者，就用我的话解释一下，我用一条线把这个 函数都分到一边，而另一边没有这个函数，很明显，
，
这两个函数都可以做到，所以函数 在 
的次梯度集合为 ![\large \left [ 0,1 \right ]](http://img.e-com-net.com/image/info8/bfee5b14adfb410aa2d83d6968cdc163.gif){kind=small}
下面用公式验证一下：
整理可得：
由此可得：
![\large g \in \left [ 0,1 \right ]](http://img.e-com-net.com/image/info8/a5b1c1fceb2a4b8fbf1a321306c34810.gif){kind=small}
次梯度存在性：
次梯度什么时候存在？
凸函数是次梯度存在的必要条件，若不是凸函数，则必然会有某些点次梯度是空集，只有是凸函数才能保证任意一点的次梯度存在
3. Bregman距离(布雷格曼距离) ：
Bregman距离概念 ：
Bregman距离，又称Bregman散度，定义如下：
表示的是 
之间的布雷格曼距离
简单说明一下，式中 
表示的就是凸函数 
，一定要是凸函数！
表示的是 
点的次梯度集合.
Bregman距离的含义 ：
我们简单的整理一下上面的布雷格曼距离公式，如下：
我们会发现其中的 
很像泰勒公式.
泰勒公式：
，把等式右边减到左边，得出：
我们发现 
时，完全一样，所以我们简易的把Bregman距离理解为：
与 
之间的Bregman距离 实际上可以理解为函数 与其一阶泰勒近似之差.
介绍了一些准备知识，下面才开始正式的开始使用LBF模型的分裂布雷格曼迭代进行水平集分割轮廓.
4. LBF模型 ：
我的方向是和牙齿分割有关，所以这里学习采用局部二元拟合(LBF)模型提取骨组织，在强度不均匀的情况下，具有较好的弱边缘提取性能。
论文中的LBF模型如下：
其中 
的定义论文中也提到了：
仔细看了一下和之前提到的 Chan-Vese 都差不多，M1(ϕ)=Hε(ϕ)，M2(ϕ)=1-Hε(ϕ)，Kσ是卷积核，和之前提到的其实大同小异.
但是，LBF模型对初始条件很敏感，因为能量函数是非凸的，可能收敛于局部极小值。此外，使用梯度体面方案的能量函数的最小化过程将是耗时的。为了解决这两个问题，我们采用了Chan等人提出的全局凸分割方法，得到了LBF模型的全局凸版本为（为什么时凸的呢？）：
其中：
，函数 
是一个边缘指示器，非常简单，其式子表示为：
也就是根据原图梯度引入的边缘指示器。
5. Split Bregman 凸优化：
看到这里，我们是要求这个凸函数的的最优解，也就是全局最优解，所以我们先把总的能量函数列出：
![\small E(u )=argmin(\iint_{}^{} g\cdot \left | \bigtriangledown u \right |dxdy+\lambda [\iint_{}^{} K\cdot \left | I-f1 \right |^{2}dxdy-\iint_{}^{} K\cdot \left | I-f2 \right |^{2}dxdy])](http://img.e-com-net.com/image/info8/b7f8a59b008842b8a0889ded39d0a259.gif){kind=small}
是水平集函数，K是卷积操作，
是图像矩阵，
为曲线内外灰度均值
首先，将用于边缘检测的全局优化凸能量函数简化为公式，公式如下：
就是要把能量函数化为上面这种形式，然后进行分裂布雷格曼算法的凸优化 ，通过以下方法将能量函数转化为上面这种形式：
之后，我们在这个求凸函数最优解问题中加入一个辅助变量 
，并且 
，这也是分裂布雷格曼问题的关键所在 . 然后在原式中引入一个二次惩罚函数 
，将约束最小化问题转化为无约束问题，原式如下 ：
通过变分原理，我们可以上述公式中的最优解为 ：
注意，正常求变分的时候，是 
的，但是上述式子中是 
，这也是Split Bregman(分裂布雷格曼)迭代算法的特别之处，就是分裂水平集梯度为 
和. 
.
1 . 利用高斯塞德尔迭代法得到了 
的近似解，论文中体现的 Gauss Seidel 迭代法为如下形式，作为如下定义：(我也自己总结了Gauss Seidel 迭代法，可以来看一看)
（ 我认为 
最后不是 
而是 
，在复现的过程中也是）
最后返回新的水平集函数 ，也就是 
.
2 . 对 的最小化使用以下公式执行：
其中 
方法为：
式中的 
就定义为：
算法（Algorithm）：
可能看到这里还是有点懵，但是作为计算机专业的同学，当看到算法流程的时候就都豁然开朗一些了 .
(初始值，
)
一开始我们知道 
，表示在迭代开始之前，
，但是我们引入了变量 。
根据步骤 2 ：使用该时刻的 
， 得出下一时刻的。
再根据步骤 3 ：我们发现通过对 
和 做和的 最小化，得出新的 ，也就是
再根据步骤 4 ：我们用上两步得到的 和 ，更新 得到新的 
.
最后设置阈值 
重置水平集函数，并更新轮廓内外灰度平均值 
也就是之前提到的
反复迭代计算，当上下两层水平集函数取 
范数时误差小于一定程度时，停止迭代.
(最后说明一下，mu是阈值，lamuda是控制收缩速度的，越小收缩越快,但是越小就导致某些地方稀碎)
实验结果（绿色结果为分割部分，参数：
，由于全局凸函数水平集初始数据我认为不重要）：
最后留下一个我的疑点，Split Bregman 迭代算法中的 
和 Bregman 距离的关系？
参考文献：
[4] Beck A. First-order methods in optimization[M]. SIAM, 2017.
[5] Nesterov Y. Introductory lectures on convex programming volume i: Basic course[J]. Lecture notes, 1998, 3(4): 5.