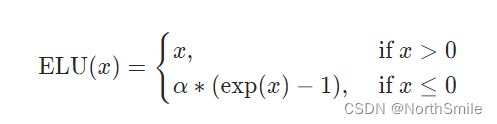常用激活函数:Sigmoid/Softmax/ELU/ReLU/LeakyReLU/Tanh...(Pytorch)
激活函数
- 一、Sigmoid
-
- 1.介绍
- 2.实例
- 二、Softmax
-
- 1.介绍
- 2.实例
- 三、ELU:指数线性单元函数
-
- 1.介绍
- 2.实例
- 四、ReLU:整流线性单元函数
-
- 1.介绍
- 2.实例
- 五、ReLU6
-
- 1.介绍
- 2.实例
- 六、LeakyReLU
-
- 1.介绍
- 2.实例
- 七、Tanh:双曲正切函数
-
- 1.介绍
- 2.实例
一、Sigmoid
1.介绍
该函数输入为任意形状,输出与输入保持一致,此操作是将所有元素映射到(0,1)范围内,推导如下:

2)调用方式
torch.nn.Sigmoid()
2.实例
sigmoid=nn.Sigmoid()
# 1.标量
# inp=torch.tensor(10,dtype=torch.float32)
# out:tensor(1.0000)
# 2.向量
# inp=torch.tensor([10,25,-2,0])
# out: tensor([1.0000, 1.0000, 0.1192, 0.5000])
# 3.二维数组
inp=torch.tensor([[10,-2],
[25,0]])
# out: tensor([[1.0000, 0.1192],
# [1.0000, 0.5000]])
out=sigmoid(inp)
print("out:",out)
二、Softmax
1.介绍
1)公式定义
公式理解:分母为输入向量中的所有元素按照指数方式求和,然后将输入中的每个元素按照指数方式除以分母得到计算结果。
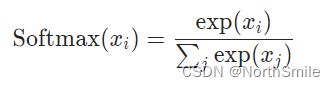
2)调用方式
该函数输入/输出为n维向量,目的是将其输入重新缩放,使其所有元素皆属于[0,1],并且此时所有元素总和为1。
torch.nn.Softmax(dim=None) # 参数dim表示softmax进行计算的维度
2.实例
1)n维向量
# 1.n维向量
softmax=nn.Softmax(dim=0)
inp=torch.tensor([10,20,5,3],dtype=torch.float32)
print("inp:",inp)
out=softmax(inp)
print("out:",out)
total_sum=torch.sum(out)
print("sum:",total_sum)
print(math.exp(inp[0])/torch.sum(torch.exp(inp)))
inp: tensor([10., 20., 5., 3.])
out: tensor([4.5398e-05, 9.9995e-01, 3.0589e-07, 4.1397e-08])
sum: tensor(1.)
tensor(4.5398e-05)
2)dim参数验证(详解见:https://blog.csdn.net/qq_43665602/article/details/126576622)
softmax=nn.Softmax(dim=0)
inp=torch.tensor([[1., 4., 8.],
[8., 0., 5.]])
print("inp:",inp)
out=softmax(inp)
print("out:",out)
total_sum=torch.sum(out)
print("sum:",total_sum)
dim=0时结果:第0维长度为2,该函数沿着列分为3个切片,分别对三个切片进行计算
inp: tensor([[1., 4., 8.],
[8., 0., 5.]])
out: tensor([[9.1105e-04, 9.8201e-01, 9.5257e-01],
[9.9909e-01, 1.7986e-02, 4.7426e-02]])
sum: tensor(3.)
dim=1时结果:第1维长度为3,该函数沿着列分为2个切片,分别对两个切片进行计算
inp: tensor([[1., 4., 8.],
[8., 0., 5.]])
out: tensor([[8.9468e-04, 1.7970e-02, 9.8114e-01],
[9.5227e-01, 3.1945e-04, 4.7411e-02]])
sum: tensor(2.)
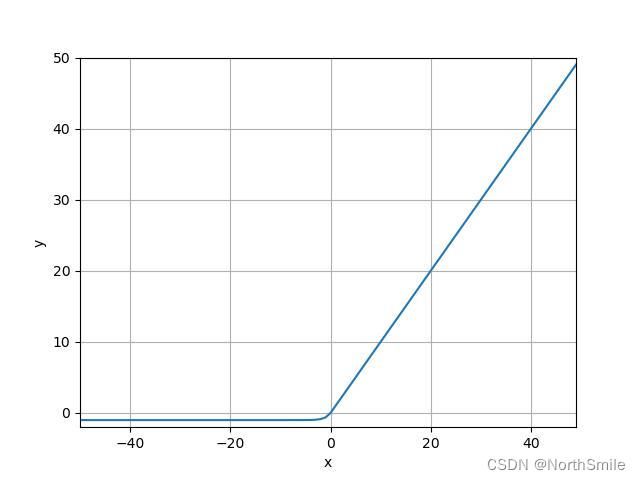
三、ELU:指数线性单元函数
1.介绍
2)调用方式
该函数是在元素级别进行操作,既将输入中所有特征元素进行公式中所示操作。该函数输入为任意形状,输出形状与输入保持一致。
torch.nn.ELU(
alpha=1.0,
inplace=False) # 该参数可选,默认为False,若为True则表示输入变量在内存中存储的值被计算结果覆盖
2.实例
1)inplace参数验证
elu=nn.ELU(inplace=False)
inp=torch.tensor(-2.5,dtype=torch.float32).to(device)
print("inp address:",id(inp)) # 查看变量在内存中的位置
out=elu(inp)
print("out address:",id(out))
print(out) # tensor(-0.9179, device='cuda:0')
print(inp) # 验证elu运算之后inp变量值是否被覆盖
inplace=False时运行结果:可看到此时输入变量和输出变量在内存中的位置不一样,说明输入变量的值没有被计算结果覆盖。
inp address: 1892728046504
out address: 1892728156304
tensor(-0.9179, device='cuda:0')
tensor(-2.5000, device='cuda:0')
inplace=True时运行结果:可看到此时输入变量和输出变量在内存中的位置一样,说明输入变量的值被计算结果覆盖,此时优点是节省内存,缺点是损失了输入值。
inp address: 1924575957856
out address: 1924575957856
tensor(-0.9179, device='cuda:0')
tensor(-0.9179, device='cuda:0')
2)输入为任意形状
# 1.标量
# inp=torch.tensor(-2.5,dtype=torch.float32).to(device)
# out1=math.exp(-2.5)-1
# print(out1) # -0.9179150013761012
# tensor(-0.9179, device='cuda:0')
# 2.向量/列表
# inp=torch.tensor([10,-2.5])
# tensor([10.0000, -0.9179])
# 3.二维数组
inp=torch.tensor([[1,-2.5],
[0,10]])
# tensor([[ 1.0000, -0.9179],
# [ 0.0000, 10.0000]])
out=elu(inp)
print(out)
四、ReLU:整流线性单元函数
1.介绍
1)公式定义及图示
公式理解:该激活函数最为常用,以y轴划分,左面恒为0,右面为y=x。

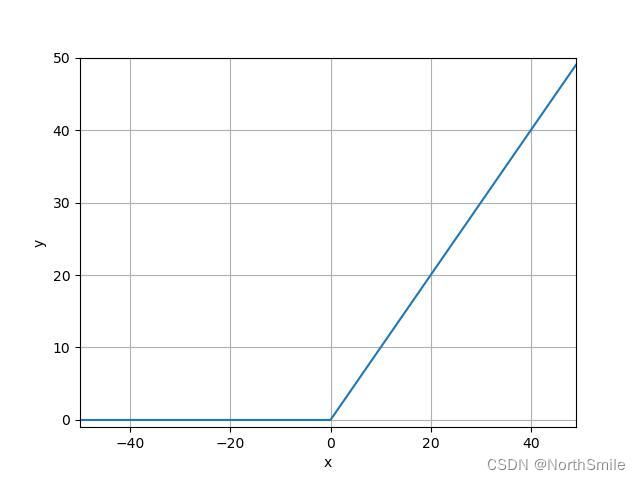
2)调用方式
- 该函数输入为任意形状,输出与输入形状保持一致;
- 操作在元素级别进行;
- inplace参数表示是否采用计算结果替换原始输入;
torch.nn.ReLU(inplace=False)
2.实例
relu=nn.ReLU()
# 1.标量
# inp=torch.tensor(2.5)
# out: tensor(2.5000)
# 2.向量
# inp=torch.tensor([2.5,0,-10,25])
# out: tensor([ 2.5000, 0.0000, 0.0000, 25.0000])
# 3.二维数组
inp=torch.tensor([[2.5,0],
[-10,25]])
# out: tensor([[ 2.5000, 0.0000],
# [ 0.0000, 25.0000]])
out=relu(inp)
print("out:",out)
五、ReLU6
1.介绍
1)公式定义及图示
公式理解:以y轴划分,左面恒为0;右面当x<=6时为y=x,此外一直保持y=6。此函数对ReLU函数的上限做了一定的限制,缩小了参数搜索范围。
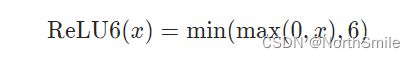

2)调用方式
- 该函数输入为任意形状,输出与输入形状保持一致;
- 操作在元素级别进行;
- inplace参数表示是否采用计算结果替换原始输入;
torch.nn.ReLU6(inplace=False)
2.实例
relu=nn.ReLU6()
# 1.标量
inp=torch.tensor(2.5)
# out: tensor(2.5000)
# 2.向量
# inp=torch.tensor([2.5,0,-10,25])
# out: tensor([ 2.5000, 0.0000, 0.0000, 6.0000])
# 3.二维数组
inp=torch.tensor([[2.5,0],
[-10,25]])
# out: tensor([[ 2.5000, 0.0000],
# [ 0.0000, 6.0000]])
out=relu(inp)
print("out:",out)
六、LeakyReLU
1.介绍
1)公式定义及图示
公式理解:定义中第二种方式更直观,解决了ReLU函数在x<0时恒为0的缺点。
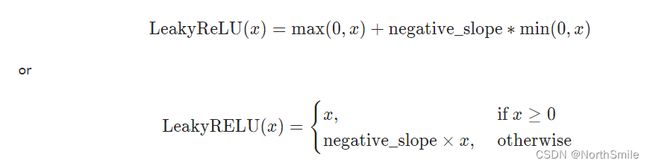

2)调用方式
- 该函数输入为任意形状,输出与输入形状保持一致;
- 操作在元素级别进行;
- inplace参数表示是否采用计算结果替换原始输入;
- negative_slope控制x<0时的斜率;
torch.nn.LeakyReLU(negative_slope=0.01, inplace=False)
2.实例
relu=nn.LeakyReLU()
# 1.标量
# inp=torch.tensor(2.5)
# out: tensor(2.5000)
# 2.向量
# inp=torch.tensor([2.5,0,-100,25])
# out: tensor([ 2.5000, 0.0000, -1.0000, 25.0000])
# 3.二维数组
inp=torch.tensor([[2.5,0],
[-100,25]])
# out: tensor([[ 2.5000, 0.0000],
# [ -1.0000, 25.0000]])
out=relu(inp)
print("out:",out)
七、Tanh:双曲正切函数
1.介绍
1)公式定义及图示
公式理解:该函数现常用于神经网络最后一层。
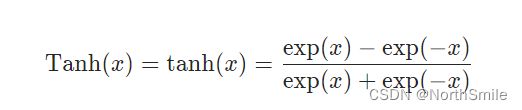

此操作是将所有元素映射到(-1,1)范围内,推导如下:

2)调用方式
- 该函数输入为任意形状,输出与输入形状保持一致;
- 操作在元素级别进行;
torch.nn.Tanh()
2.实例
tanh=nn.Tanh()
# 1.标量
inp=torch.tensor(2.5)
# out: tensor(0.9866)
# 2.向量
# inp=torch.tensor([2.5,0,-10,25])
# out: tensor([ 0.9866, 0.0000, -1.0000, 1.0000])
# 3.二维数组
# inp=torch.tensor([[2.5,0],
# [-10,25]])
# out: tensor([[ 0.9866, 0.0000],
# [-1.0000, 1.0000]])
out=tanh(inp)
print("out:",out)