模糊综合评价模型
声明:本文以数学建模清风老师的课程与课件为基础并且借鉴了一位同学的博客,加上个人理解最终写成,如果文章中有错误的地方欢迎各位在评论区指正。
一.引子
1.数学归纳法:同高中知识
2.秃子悖论:秃子悖论
这俩个例子都是类似于“量变引起质变”的道理,而在数学中我们把这类问题的性质叫做“模糊性”,在生活中我们也经常能遇到一些模糊的概念,比如年轻、帅、很少很多…
二.基本知识与概念
模糊综合评价法是一种基于模糊数学的综合评价方法。该综合评价法根据模糊数学的隶属度理论把定性评价转化为定量评价,即用模糊数学对受到多种因素制约的事物或对象做出一个总体的评价。它具有结果清晰,系统性强的特点,能较好地解决模糊的、难以量化的问题,适合各种非确定性问题的解决。——来自百度百科
1.模糊集合:
模糊集合是用来描述模糊性概念的集合,它与经典集合(高中课本中所学到的集合)的区别之一是,模糊集合不具备确定性,例如35岁,我们既可以认为它“年轻”,也可以认为它是“不年轻”。
而在数学中,我们用隶属函数对模糊集合进行描述。隶属函数是隶属度对各个元素的函数,定义域是我们所研究的元素,函数值就是隶属度。隶属度的范围是[0,1],其值越大,就代表越属于这个集合。
2.模糊集合的分类:
偏小型:年轻、小、冷
中间型:中年、中、暖
偏大型:老年、大、热
三.隶属函数的三种确定方法
1.模糊统计法:(需要去做统计、发问卷调查,数模比赛使用很少)
找多个人对同一个模糊概念进行描述。
2.借助已有的客观尺度:(需要有合适的指标,并且能够收集到数据)
对于某些模糊集合,我们可以用已经有的指标去作为元素的隶属度。例如对于“小康家庭”这个模糊集合,我们想确定100户家庭的隶属度,那就可以用“恩格尔系数”衡量相应的隶属度。恩格尔系数=食品支出总额/家庭总支出,家庭越接近小康水平,其恩格尔系数应该越低,那“恩格尔系数”就越大,我们便可以把“恩格尔系数”看作家庭相对于“小康家庭”的隶属度。
| 论域 | 模糊集 | 隶属度 |
|---|---|---|
| 设备 | 设备完好 | 设备完好率 |
| 产品 | 质量稳定 | 正品率 |
| 家庭 | 小康家庭 | 恩格尔系数 |
3.指派法(主观性较强但是简单方便)
根据问题性质直接套用某些分布作为隶属函数


其中,我们对梯形分布使用较多,并且使用梯形分布最简单。 可以通过下面一道例题来进一步理解。
例:已知某一天的 S O 2 SO_{2} SO2 的浓度为0.07mg/ m 3 m^3 m3,大气污染物中关于 S O 2 SO_{2} SO2 的评价标准如下表,试确定 S O 2 SO_{2} SO2 在每一个等级中的隶属度。
| Ⅰ | Ⅱ | Ⅲ | Ⅳ |
|---|---|---|---|
| 0.05 | 0.15 | 0.25 | 0.50 |
解:根据 偏向指定值 可将几个等级划分为,I级为偏小型,Ⅱ级和Ⅲ级为中间型,Ⅳ级为偏大型。
定义 A 1 A_{1} A1为Ⅰ级的隶属函数, A 2 A_{2} A2为Ⅱ级的隶属函数, A 3 A_{3} A3为 Ⅲ 级的隶属函数, A 4 A_{4} A4为 Ⅳ 级的隶属函数。
可得如下算术式:
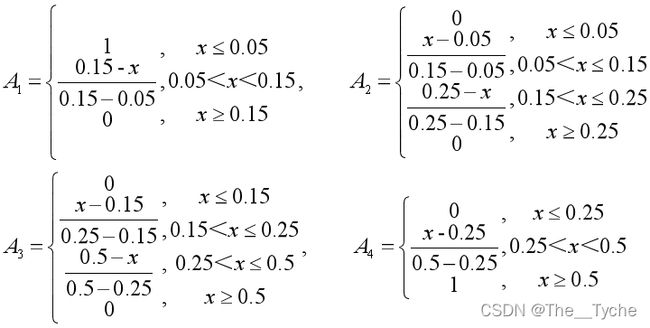
则题目所给“某一天” S O 2 SO_{2} SO2的隶属度为:、
A 1 A_{1} A1(0.07)=0.8, A 2 A_{2} A2(0.07)=0.2, A 3 A_{3} A3(0.07)=0, A 4 A_{4} A4(0.07)=0
四.应用:模糊综合评价
1.评价问题概述
(1)模糊评价问题是要解决的问题是:
①把论域(感兴趣的研究的对象,如一个班上的50名同学)中的对象(如班上的每一名学生)对应评语集(优良差)中的一个指定的评语 。或者
②将方案作为评语集并选择一个最优的方案。
(2)在模糊综合评价中,我们引入了三个集合:
因素集(评价指标集) U = {u1,u2,…,un}
评语集(评价的结果集) V = {v1,v2,…,vm}
权重集(指标的权重) A = {a1,a2,…,an}
例如,我们在评价一名学生时,可以引入这样的三个集合:
因素集 U = {专业排名,课外实践,志愿服务,竞赛成绩},
评语集 V = {优,良,差},
权重集 A = {0.5,0.1,0.1,0.3}
2. 一级模糊综合评价:
一级模糊综合评价分为以下五个步骤:
①确定因素集
②确定评语集
③确定各因素的权重
④确定模糊综合判断矩阵
⑤综合评判
例题如下:
例一:一级模糊综合评价在人事考核中的应用(见《数学建模算法与应用》P375)
按照上面的分析,我们可以将这个问题分解成下面的五个步骤:
第一步:确定因素集
对员工的表现,需要从多个方面(找出多个评价指标)进行综合评判,如员工的工作业绩、工作态度、沟通能力、政治表现等。所有这些因素构成了评价指标体系集合,即因素集。
记为: U = { u 1 , u 2 , u 3 , u 4 } U = \lbrace u_{1},u_{2},u_{3},u_{4}\rbrace U={u1,u2,u3,u4}
注:一级模糊评价中,n 往往较小(一般 ≤ 5)且 指标间相关性不强
在本题中我们可以取: U = { 工 作 业 绩 u 1 , 工 作 态 度 u 2 , 沟 通 能 力 u 3 , 政 治 表 现 u 4 } U = \lbrace 工作业绩u_{1},工作态度u_{2},沟通能力u_{3},政治表现u_{4}\rbrace U={工作业绩u1,工作态度u2,沟通能力u3,政治表现u4}
第二步:确定评语集
由于每个指标的评价值的不同,往往会形成不同的等级。如对工作业绩的评价有好、较好、中等、较差、很差等。由各种不同决断构成的集合称为评语集。
记为: V = { v 1 , v 2 , v 3 , v 4 , v 5 } V = \lbrace v_{1},v_{2},v_{3},v_{4},v_{5}\rbrace V={v1,v2,v3,v4,v5}
注:评语集中有 m 个元素, m 与因素集中的 n 无关
在本题中可以取: V = { 优 秀 v 1 , 良 好 v 2 , 一 般 v 3 , 较 差 v 4 , 差 v 5 } V = \lbrace 优秀v_{1},良好v_{2},一般v_{3},较差v_{4},差v_{5}\rbrace V={优秀v1,良好v2,一般v3,较差v4,差v5}
第三步:确定各因素的权重
一般情况下,因素集中的各因素在综合评价中所起的作用是不相同的,综合评价结果不仅与各因素的评价有关,而且在很大程度上还依赖于各因素对综合评价所起的作用,这就需要确定一个各因素之间的权重分配,它是U上的一个模糊向量。
记为: A = { a 1 , a 2 , a 3 , a 4 , a 5 } a i A = \lbrace a_{1},a_{2},a_{3},a_{4},a_{5}\rbrace a_{i} A={a1,a2,a3,a4,a5}ai表示第 i 个因素的权重,并且 ∑ i = 1 n a i = 1 \sum_{i=1}^n \ a_{i} =1 ∑i=1n ai=1
确定权重的方法有:Delphi法(专家调查法)、加权平均法、众人评估法。(数学建模一般不用)
在数学建模中,如果没有数据我们就用层次分析法,如果有数据我们就用熵权法。
假设在本题中我们通过层次分析法or熵权法得到了权重,记作: A = [ 0.25 , 0.2 , 0.25 , 0.3 ] A = [0.25,0.2,0.25,0.3] A=[0.25,0.2,0.25,0.3]
第四步:确定模糊综合判断矩阵
对于指标 u i u_{i} ui来说,对各个评语的隶属度为V上的模糊子集。对指标 u i u_{i} ui的评判记为:
R i = [ r i 1 , r i 2 , . . . , r i m ] R_{i}=[r_{i1},r_{i2},...,r_{im}] Ri=[ri1,ri2,...,rim] (其中 r i 1 r_{i1} ri1表示 u i u_{i} ui对评语1的隶属度, r i m r_{im} rim表示 u i u_{i} ui对评语m的隶属度,以此类推)。
求出若干个 R i R_{i} Ri得到模糊综合判断矩阵 R = ( r 11 r 12 ⋯ r 1 m r 21 r 22 ⋯ r 2 m ⋮ ⋮ ⋱ ⋮ r n 1 r n 2 ⋯ r n m ) = ( R 1 R 2 ⋮ R n ) R=\begin{pmatrix} r_{11} & r_{12} & \cdots & r_{1m} \\ r_{21} & r_{22} & \cdots & r_{2m} \\ \vdots & \vdots & \ddots & \vdots \\ r_{n1}& r_{n2} & \cdots & r_{nm} \\ \end{pmatrix}=\begin{pmatrix}\\R_{1}\\R_{2}\\ \vdots\\ R_{n}\end{pmatrix} R=⎝⎜⎜⎜⎛r11r21⋮rn1r12r22⋮rn2⋯⋯⋱⋯r1mr2m⋮rnm⎠⎟⎟⎟⎞=⎝⎜⎜⎜⎛R1R2⋮Rn⎠⎟⎟⎟⎞
在本题中:
① u1(工作业绩)可以由群众评议打分来确定:
参与打分的群众中,有10%的人认为该员工政治表现优秀,50%的人认为政治表现良好,40%的人认为政治表现一般,认为政治表现较差或差的人为0,由此我们可以得到 R1 = [0.1,0.5,0.4,0,0]
同理可得:
② u2(工作态度),u3(沟通能力),由部门领导打分来确定:
R2 = [ 0.2,0.5 ,0.2,0.1,0 ],R3= [ 0.2,0.5,0.3,0,0 ]。
③ u4(政治表现)由单位考核组成员打分来确定:
R4= [ 0.2,0.6,0.2,0,0]。
⑤综合R1,R2,R3,R4我们可以得到评价矩阵:

第五步:模糊综合评判
进行矩阵合成运算,得到综合评判结果: B = A ⋅ R B=A \cdot R B=A⋅R
综合后的评判结果记作 B = [ b 1 , b 2 , . . . b n ] B=[ b_{1},b_{2},...b_{n} ] B=[b1,b2,...bn]
(其中 b i b_{i} bi的含义是要评价的对象对于评语 i 的隶属度。如果我们发现 b k = m a x [ b 1 , b 2 , . . . b n ] b_{k}=max[ b_{1},b_{2},...b_{n} ] bk=max[b1,b2,...bn](说明要评价的对象对于评语k的隶属度最大)而隶属度代表了相符程度,那么,我们就应该把要评价的对象划分到评语 k 这一类)。
在本题中:

得到:B = [0.175,0.53,0.275,0.02,0]
隶属度0.175对应上面 “第二步” 的优秀,隶属度0.53对应良好,隶属度0.275对应一般,
隶属度0.02对应较差,隶属度0对应差。
取隶属度数值最大的评语作为此次综合评判的结果。其中0.53最大,则结果为“良好”。
例二:空气质量
(此处并非原创,引用自)
下表给出了大气污染物评价标准,今测得某日某地表中这些污染物日均浓度依次为:(0.07,0.20,0.123,5.00,0.08,0.14)。各污染物权重确定为:(0.1,0.2,0.3,0.3,0.05,0.05)。试评价当天空气质量等级。

解:
第一步:取因素集: U = {SO2,TSP,NOx,CO,PM1,O3}
第二步:取评语集: V = {I级,Ⅱ级,Ⅲ级,Ⅳ级}
第三步:确定各因素权重:A = [ 0.1,0.2,0.3,0.3,0.05,0.05]
第四步:确定模糊综合评判矩阵:选用指派法中的梯形分布,其中I级为偏小型,Ⅱ级和Ⅲ级为中间型,Ⅳ级为偏大型。
污染物i对空气质量各等级的隶属函数(梯形分布)如下:
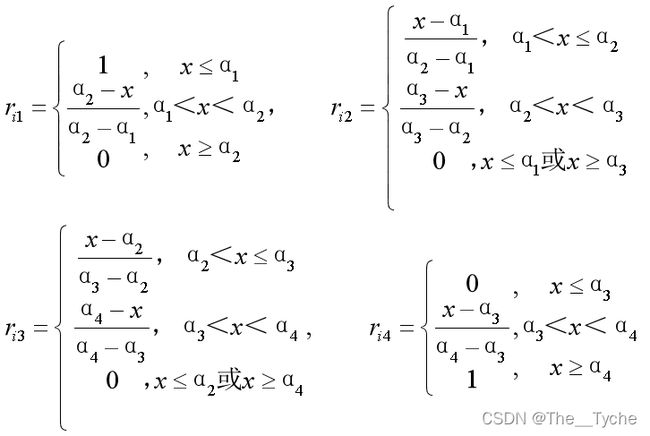
代入数据求得模糊综合评判矩阵:
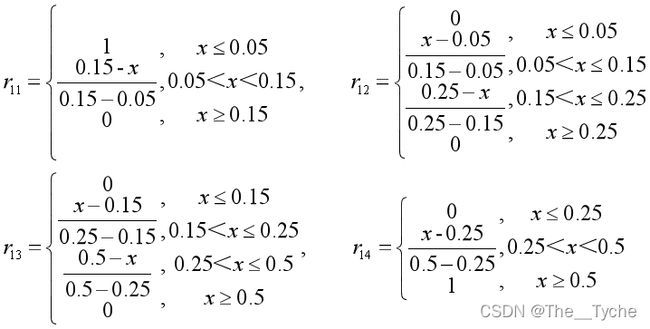
SO2,TSP,NOx,CO,PM1,O3的浓度分别为 ( 0.07,0.20,0.123,5.00,0.08,0.14),
拿 SO2 为 0.07mg/m3 举例:
![]()
其他污染物以此类推,最终的模糊综合评判矩阵为:
第五步:综合评判:
例三:露天煤矿选择方案
解:
第一步:取因素集:可采矿量、基建投资、采矿成本、不稳定费用、净观值
第二步:取评语集:5种方案
第三步:确定各因素权重:在这道题目的答案中,专家给出了权重A=(0.25,0.20,0.20,0.10,0.25)。如果我们没有专家给出的数值,我们可以用熵权法确定。
第四步:确定模糊综合评判矩阵:在这道题目的答案中,他没有用我们已有的公式,而是借助一些已有标准自己创建了一些隶属函数。如,在实际中可采矿量和净观值是越大越好,我们设计一种“偏大型”的隶属函数,基建投资、采矿成本和不稳定费用越小越好,我们就设计一种“偏小型”的隶属函数(最后也要转化成偏大型,答案中是用“1-x/8000”的方式)。
隶属函数不唯一只要合理便可,为了“合理”我们可以在论文中这样写:根据专家建议、根据某某某的论文公式。

第五步:综合评判:

最后得出结论的时候我们可以用直方图等统计图来使论文更丰满。
总结:①本题所给答案中隶属函数的求法是:借助已有的客观尺度。
②因素集中基建投资、采矿成本一级不稳定费用是极小型指标,因此就需要在隶属度函数那里做一些处理,使其变成极大型。
③当隶属函数求值只用梯形分布最终的隶属度和为1,用其他方法求隶属度会使得最终的隶属度和不为1,但不影响最终的评判效果。
3. 多级模糊综合评价:(本质是转化成一级模糊综合评价)
概念:将因素进行分类,分别对每一类因素进行综合评判,再对评价结果在各类之间进行更高层次综合的评价方法。
为什么要引入多级模糊综合评价模型:如果因素集中指标较多,我们则需要对其进行归类来简化计算,这里就要用到我们的多级模糊综合评价。
划分原则:看哪俩个指标有相关性就把他们划分在一起,同一级的权重之和为 1 。
例一:二级模糊综合评价——评选奖学金:
评价学⽣的表现并作为奖学金的评判标准。
因素集 U = { 专业课成绩、非专业课成绩、国家竞赛成绩、省级竞赛成绩、校级竞赛成绩、国家级奖项、省级奖项、校级奖项、志愿服务}
评语集 V = {一等,二等,无奖学金}
我们对这些因素分类可得:
![]()
对于多级模糊评价,我们需要对每一个大的 U i U_{i} Ui都做一次一级模糊综合评价。
例如,我们对学习成绩 U 1 U_{1} U1做一级模糊综合评价:
①因素集: U 1 = [ 专 业 课 成 绩 u 1 , 非 专 业 课 成 绩 u 2 ] U_{1}= [ 专业课成绩u_{1},非专业课成绩u_{2} ] U1=[专业课成绩u1,非专业课成绩u2]
②评语集: V = [ v 1 一 等 , v 2 二 等 , v 3 无 奖 学 金 ] V = [v_{1}一等,v_{2}二等,v_{3}无奖学金] V=[v1一等,v2二等,v3无奖学金]
③确定权重: A 1 = [ 0.6 , 0.4 ] A_{1}= [0.6,0.4] A1=[0.6,0.4]
④评判矩阵:假如我们通过问卷方式得到了: R 1 = ( 0.8 0.2 0 0.7 0.3 0 ) R_{1}=\begin{pmatrix}\\0.8 &0.2&0\\0.7&0.3&0\end{pmatrix} R1=(0.80.70.20.300)。
⑤综合评判: B 1 = R 1 ⋅ A 1 = [ 0.76 , 0.24 , 0 ] B_{1}=R_{1} \cdot A_{1}=[0.76,0.24,0] B1=R1⋅A1=[0.76,0.24,0]
同理,我们可以得到关于竞赛成绩的 B 2 B_{2} B2、关于个人荣誉的 B 3 B_{3} B3、关于志愿服务的 B 4 B_{4} B4
构成: R = ( B 1 B 2 B 3 B 4 ) = ( 0.76 0.24 0 0.15 0.27 0.28 0.4 0.2 0.4 0.1 0.8 0.1 ) R=\begin{pmatrix}\\B_{1} \\B_{2}\\B_{3}\\B_{4}\end{pmatrix}=\begin{pmatrix}\\0.76&0.24&0 \\0.15&0.27&0.28\\0.4&0.2&0.4\\0.1&0.8&0.1\end{pmatrix} R=⎝⎜⎜⎛B1B2B3B4⎠⎟⎟⎞=⎝⎜⎜⎛0.760.150.40.10.240.270.20.800.280.40.1⎠⎟⎟⎞ ,又由于 A = [ 0.4 , 0.3 , 0.2 , 0.1 ] A=[0.4,0.3,0.2,0.1] A=[0.4,0.3,0.2,0.1]
则 B = A ⋅ R = [ 0.439 , 0.297 , 0.264 ] B= A \cdot R =[0.439,0.297,0.264] B=A⋅R=[0.439,0.297,0.264] 。 由于0.439最大,所以该同学应该领一等奖学金。
拓展与思考:如果全年级有100名同学,但只有3名同学可以获得一等奖学金,那该如何评选?答:对每名同学进行综合评判,选取对于一等奖学金隶属度最高的三名同学。
例二:三级模糊综合评价——陶瓷厂产品销量评判:
对某陶瓷厂生产的6种产品的销售前景进行评判。
解:
第一步:确定因素集:从产品情况、销售能力、市场需求三方面考虑
第二步:确定评语集:V=[1,2,3,4,5,6]表示6种不同的陶瓷产品
第三步:确定各因素权重:根据专家评判法得到下图

第四步:确定模糊综合判断矩阵(在比赛中这些数据往往需要参赛者自己找)

取出运行费用的评价矩阵 R 23 R_{23} R23对运行费用进行一级模糊综合评价:
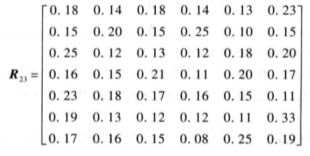
权重分配为: A = [ 0.2 , 0.15 , 0.10 , 0.10 , 0.20 , 0.15 , 0.10 ] A=[0.2,0.15,0.10,0.10,0.20,0.15,0.10] A=[0.2,0.15,0.10,0.10,0.20,0.15,0.10]
则 B 23 = A 23 ⋅ R 23 = [ 0.1910 , 0.1565 , 0.1595 , 0.1465 , 0.1505 , 0.1960 ] B_{23}=A_{23} \cdot R_{23}=[0.1910,0.1565,0.1595,0.1465,0.1505,0.1960] B23=A23⋅R23=[0.1910,0.1565,0.1595,0.1465,0.1505,0.1960]
将运行费用的一级评判结果作为二级销售能力评判矩阵的第三行,对销售能力进行二级评判:

同理可以对市场需求和产品情况进行二级模糊综合评价,得到B1和B3
第五步:综合评判

从计算结果可以看出,产品6综合评分最高,其次为产品4,以下依次为产品5、3、1、2(再配一张条形图或柱状图更直观)
研究结果表明:商家应该对产品6加大投资,其次为产品4,产品5、3、1、2销售前景不乐观,应减少投资。
注意:隶属函数的选取必须符合正向化的过程,例如上文“一级模糊综合评价例三”中隶属函数 “1-x/8000” 的处理方式