算法之回溯
1. 回溯（Back Tracking）
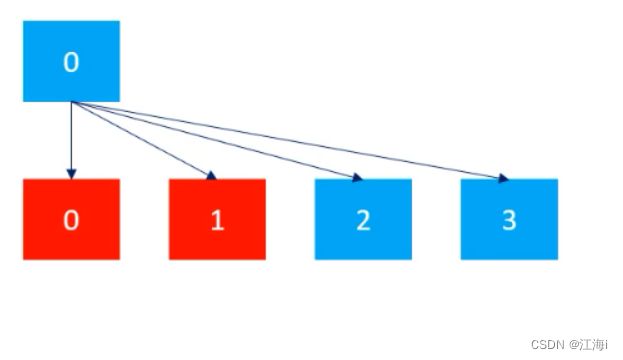
通过选择不同的岔路口来通往目的地。
每一步都选择一条路出发，能进则进，不能进就回退上一步（回溯），换一条路再试。
树前序遍历和图的深度优先搜索都是很经典的回溯应用。
2. N皇后问题（N Queens）
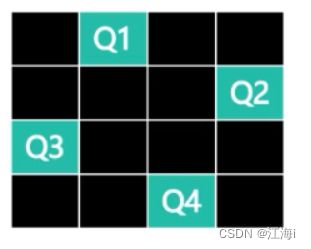
在N xN的国际象棋格子上摆放N个皇后，使其不能相互攻击，即任意两个皇后都不能处于同一行、同一列以及同一斜线上。求有多少种摆法。
2.1 回溯四皇后
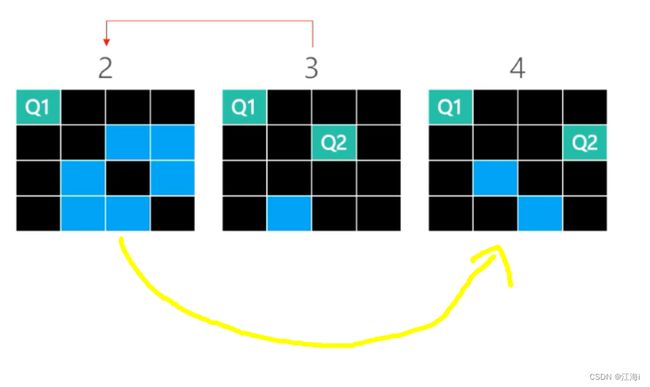
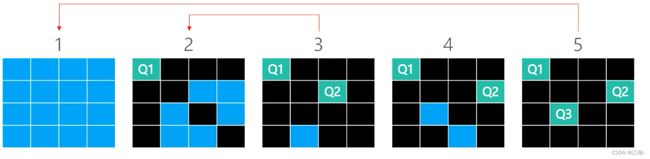
先缩少问题规模，尝试解决四皇后问题。因为棋盘的行数和皇后的个数是相同的，必须先符合每行可以放下一个皇后的前提。
-
初始棋盘：
-
针对初始棋盘，使用回溯法，任意选择一条路（第一行的某个格子）。先放入Q1：
-
再在符合条件的任意位置种放入Q2：
-
发现无法达到目的，进行回溯，选择不同的路：
-
尝试放入Q3：
-
发现放入Q3之后该路径无法达到目的，往上回溯，第二步中Q2的所有符合的位置已经用完，因此直接回溯到第一步重新选择Q1的位置：
-
Q1重新选择位置：
-
Q2：
-
Q3：
-
Q4：
-
求得四皇后的其中一个解。
2.2 四皇后 - 剪枝（Pruning）
- 这里再进行加入第一个皇后Q1的时候，放入到0号位置，同一列和同一对角线不能再放入其它的皇后，可以直接排除掉，这个过程称为剪枝。
剪枝后：
2.3 N 皇后代码实现
- n皇后代码实现
/**
* @Description n皇后问题
* @date 2022/5/19 14:57
*/
public class Queens {
public static void main(String[] args) {
new Queens().placeQueens(4);
}
// 索引 = 行号；元素值 = 列号；
// cols[4] = 5 即第四行第五列
int[] cols;
// 统计摆法
int ways;
/**
* n 皇后问题
* @param n
*/
void placeQueens(int n){
if (n < 1) return;
// 初始化数组值
cols = new int[n];
place(0);
System.out.println(ways);
}
/**
* 从第 row 行开始摆放皇后
* @param row 行
*/
void place(int row){
// 如果上一行摆放成功了，即符合所有摆放条件，最后一行不需要调用。
if (row == cols.length) {
show();
ways++;
return;
}
for (int col = 0; col < cols.length; col++) {
if (isValid(row,col)){
// 摆放皇后
cols[row] = col;
// 在下一行摆放皇后
place(row + 1);
// 回溯
// 如果将某行的所有可能都摆放完了，会返回到他的上行中，对这行重新摆放，就实现了回溯
}
}
}
/**
* 判断 row 行 col 列是否可以摆放，即判断是否需要剪枝
* @param row
* @param col
* @return
*/
boolean isValid(int row, int col){
for (int i = 0; i < row; i++) {
// 判断当前列是否有皇后
if (cols[i] == col) return false;
// 判断斜线是否有皇后
// 要添加的行号减去当前的行号 与 要添加的列号减去当前的列号的绝对值 相等就存在同一斜线。
// 即斜率 x = y
if (row - i == Math.abs(col - cols[i])) return false;
}
return true;
}
/**
* 打印摆法，有 1，无 0
*/
void show(){
for (int row = 0; row < cols.length; row++) {
for (int col = 0; col < cols.length; col++) {
if (cols[row] == col){
System.out.print("1 ");
}else {
System.out.print("0 ");
}
}
System.out.println();
}
System.out.println("-------------------");
}
}
- 修改
isValid()打印出行号和列号，可以完美的看出回溯的过程。
boolean isValid(int row, int col){
for (int i = 0; i < row; i++) {
// 判断当前列是否有皇后
if (cols[i] == col) {
System.out.println("[" + row + "][" + col + "] = false");
return false;
}
// 判断斜线是否有皇后
// 要添加的行号减去当前的行号 与 要添加的列号减去当前的列号的绝对值 相等就存在同一斜线。
// 即斜率 x = y
if (row - i == Math.abs(col - cols[i])) return false;
}
System.out.println("[" + row + "][" + col + "] = true");
return true;
}
2.4 优化 - 成员变量
- 成员变量：
// 判断当前行中是否已经存在皇后
// cols[0] = true 即 0 行已经存在皇后
boolean[] cols;
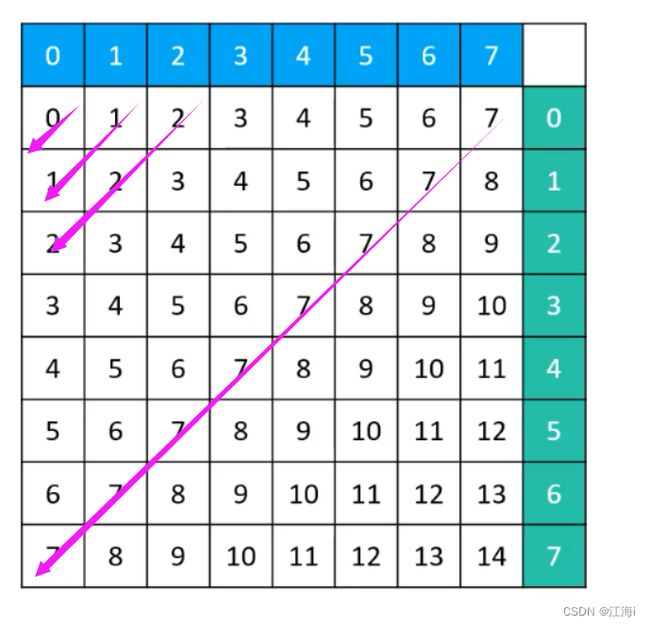
// 判断 左上角 到 右下角 是否有皇后 即 ↘ 方向
boolean[] leftTop;
// 判断 右上角 到 左下角 是否有皇后 即 ↙ 方向
boolean[] rightTop;
- 初始化成员变量：
// 初始化数组值
cols = new boolean[n];
leftTop = new boolean[(n << 1) - 1];
rightTop = new boolean[(n << 1) - 1];
可以计算出：斜线的数量为2n - 1。
- 计算斜线索引公式：
- 左上 -> 右下：
row - col + n - 1
- 右上 -> 左下：
row + col
- 实现
/**
* @Description 成员变量优化 n 皇后
* @date 2022/5/19 19:38
*/
public class QueensVar {
public static void main(String[] args) {
new QueensVar().placeQueens(4);
}
// 判断当前列中是否已经存在皇后
// cols[0] = true 即 0 列已经存在皇后
boolean[] cols;
// 判断 左上角 到 右下角 是否有皇后 即 ↘ 方向
boolean[] leftTop;
// 判断 右上角 到 左下角 是否有皇后 即 ↙ 方向
boolean[] rightTop;
// 统计摆法
int ways;
/**
* n 皇后问题
* @param n
*/
void placeQueens(int n){
if (n < 1) return;
// 初始化数组值
cols = new boolean[n];
leftTop = new boolean[(n << 1) - 1];
rightTop = new boolean[(n << 1) - 1];
place(0);
System.out.println(ways);
}
/**
* 从第 row 行开始摆放皇后
* @param row 行
*/
void place(int row){
// 如果上一行摆放成功了，即符合所有摆放条件，最后一行不需要调用。
if (row == cols.length) {
ways++;
return;
}
for (int col = 0; col < cols.length; col++) {
// 不能摆就返回
if (cols[col]) continue;
int lIndex = row - col + cols.length - 1;
int rIndex = row + col;
if (leftTop[lIndex]) continue;
if (rightTop[rIndex]) continue;
// 摆放皇后
cols[col] = true;
leftTop[lIndex] = true;
rightTop[rIndex] = true;
// 在下一行摆放皇后
place(row + 1);
// 回溯
// 如果将某行的所有可能都摆放完了，会返回到他的上行中，对这行重新摆放，就实现了回溯;
// 对于布尔类型，回溯时需要重置
// 如果不重置，回溯之后的值也会是true，即已经存在皇后的情况，永远无法摆放。
cols[col] = false;
leftTop[lIndex] = false;
rightTop[rIndex] = false;
}
}
}
2.5 优化 - 位运算
将布尔类型数组变为
byte类型和short类型变量，但不适用于较多皇后情况，只针对4或者8皇后情况。
- 修改成员变量
// 判断当前列中是否已经存在皇后
// 使用八位二字节代表列：10000000：代表第0列有皇后
byte cols;
// 判断 左上角 到 右下角 是否有皇后 即 ↘ 方向
// 使用 十六位 四字节
short leftTop;
// 判断 右上角 到 左下角 是否有皇后 即 ↙ 方向
// 使用 十六位 四字节
short rightTop;
- 实现
/**
* @Description 位运算优化 8 / 4 皇后问题
* @date 2022/5/19 19:38
*/
public class QueensBit {
public static void main(String[] args) {
new QueensBit().place8Queens();
}
// 判断当前行中是否已经存在皇后
// 使用八位二字节代表行：10000000：代表第0列有皇后
byte cols;
// 判断 左上角 到 右下角 是否有皇后 即 ↘ 方向
// 使用 十六位 四字节
short leftTop;
// 判断 右上角 到 左下角 是否有皇后 即 ↙ 方向
// 使用 十六位 四字节
short rightTop;
// 统计摆法
int ways;
/**
* n 皇后问题
*/
void place8Queens(){
place(0);
System.out.println(ways);
}
/**
* 从第 row 行开始摆放皇后
* @param row 行
*/
void place(int row){
// 如果上一行摆放成功了，即符合所有摆放条件，最后一行不需要调用。
if (row == 8) {
ways++;
return;
}
for (int col = 0; col < 8; col++) {
// 不能摆就返回
int colV = 1 << col;
int lv = 1 << (row - col + 7);
int rv = 1 << (row + col);
if ((cols & colV) != 0) continue;
if ((leftTop & lv) != 0) continue;
if ((rightTop & rv) != 0) continue;
// 摆放皇后
cols |= colV;
leftTop |= lv;
rightTop |= rv;
// 在下一行摆放皇后
place(row + 1);
// 回溯
// 如果将某行的所有可能都摆放完了，会返回到他的上行中，对这行重新摆放，就实现了回溯;
// 回溯时需要重置
cols &= ~colV;
leftTop &= ~lv;
rightTop &= ~rv;
}
}
}