频域图像增强算法

    人类传递信息的主要媒介是语言和图像。据统计在人类接受的各种信息中视觉信息占80%，所以图像信息是十分重要的信息传递媒体和方式。图像传递系统包括图像采集、图像压缩、图像编码、图像存储、图像通信、图像显示这六个部分。在实际应用中每个部分都有可能导致图像品质变差，使图像传递的信息无法被正常读取和识别。例如，在采集图像过程中由于光照环境或物体表面反光等原因造成图像整体光照不均，或是图像采集系统在采集过程中由于机械设备的缘故无法避免的加入采集噪声，或是图像显示设备的局限性造成图像显示层次感降低或颜色减少等等。因此研究快速且有效地图像增强算法成为推动图像分析和图像理解领域发展的关键内容之一。

    图像增强处理是数字图像处理的一个重要分支。很多由于场景条件的影响图像拍摄的视觉效果不佳，这就需要图像增强技术来改善人的视觉效果，比如突出图像中目标物体的某些特点、从数字图像中提取目标物的特征参数等等，这些都有利于对图像中目标的识别、跟踪和理解。图像增强处理主要内容是突出图像中感兴趣的部分，减弱或去除不需要的信息。这样使有用信息得到加强，从而得到一种更加实用的图像或者转换成一种更适合人或机器进行分析处理的图像。图像增强的应用领域也十分广阔并涉及各种类型的图像。例如，在军事应用中，增强红外图像提取我方感兴趣的敌军目标；在医学应用中，增强X射线所拍摄的患者脑部、胸部图像确定病症的准确位置；在空间应用中，对用太空照相机传来的月球图片进行增强处理改善图像的质量；在农业应用中，增强遥感图像了解农作物的分布；在交通应用中，对大雾天气图像进行增强，加强车牌、路标等重要信息进行识别；在数码相机中，增强彩色图像可以减少光线不均、颜色失真等造成的图像退化现象。

    图像工程是一门综合学科，它的研究内容非常广泛，覆盖面也很大。从1996年起，《中国图像图形学报》上连续刊登了对图像工程文献统计分类的综述文章。根据各文献的主要内容将其分别归入图像处理、图像分析、图像理解、技术应用和综述5个大类，并在此基础上对国内15种有关图像工程的重要中文期刊进行了各期刊各类文献的统计和分析。选取的刊物名有:《CT理论与应用研究》、《测绘学报》、《电子测量与仪器学报》、《电子学报》、《电子与信息学报》、《计算机学报》、《模式识别与人工智能》、《数据采集与处理》、《通信学报》、《信号处理》、《遥感学报》、《中国生物医学工程学报》、《中国体视学与图像分析》、《中国图象图形学报》、《自动化学报》。

从中我们挑选了最近5年的统计数据：在2005年的112期上发表的2734 篇学术研究和技术应用文献中，属于图像工程领域的文献有656篇。在2006年

的112期上发表的3013篇学术研究和技术应用文献中，属于图像工程领域的文献有711篇。在2007年的118期上发表的3312篇学术强究和技术应用文献中，属于图像工程领域的文献有895篇。在2008年的120期上发表的3359篇学术研究和技术应用文献中，属于图像工程领域的文献有915篇，2009年的134期上发表的3604篇学术研究和技术应用文献中，有1008篇属于图像工程领域的文献。这些统计数据显示，无论是论文总数还是选取总数都是逐年增长的。论文总数的增长表明刊物的不断发展，选取总数的增加表明图像工程的研究和应用的不断壮大。据统计从1995年至2009年，发表图像处理的文章总计2720篇，占图像工程总体的33.1%；发表图像分析的文章总计2434篇，占图像工程总体的29.6%；发表图像理解的文章总计1192篇，占图像工程总体的14.5%；发表技术应用文章1797篇，占图像工程总体的21.9%；发表综述评论文章74篇，占图像工程总体的0.9%，其中关于图像增强技术方面的文章增长率尤其较高。因此图像增强技术在今后一段时间内仍将是一个热点。

　　影响图像质量清晰程度有很多因素，室外光照度不均匀会造成图像灰度过于集中；摄像头获得的图像经过数/模转换，线路传输时都会产生噪声污染，图像质量不可避免降低，轻者变现为图像伴有噪点，难于看清图像细节；重者图像模糊不清，连大概物体面貌轮廓都难以看清。因此，对图像进行分析处理之前，必须对图像进行改善，即增强图像。图像增强并不考虑图像质量下降的原因，只是将图像中感兴趣的重要特征有选择性的突出出来，同时衰减不需要的特征，目的就是提高图像的可懂度。

　　图像增强的方法分为空域法和频域法两种，空域法是对图像中的像素点进行操作，用公式描述如下：

　　G(x,y)=F(x,y) H(x,y)

　　其中是F(x,y)原图像；H(x,y)为空间转换函数；G(x,y)表示进行处理后的图像。

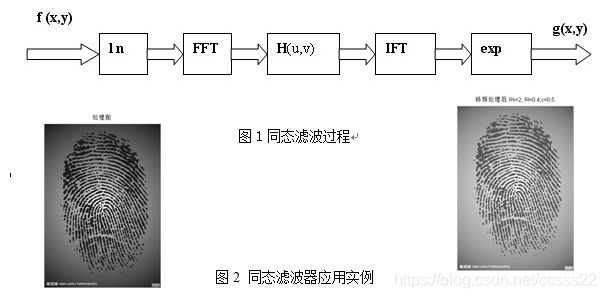
频域法是间接的处理方法，是先在图像的频域中对图像的变换值进行操作，然后变回空域。例如,先对图像进行傅里叶变化到频域，再对图像的频谱进行某种滤波修正，最后将修正后的图像进行傅里叶反变化到空域，以此增强图像。可用图1来描述该过程。

 

第二章 频域图像的原理

2.1 引言

   在进行图像处理的过程中，获取原始图像后，首先需要对图像进行预处理，因为在获取图像的过程中，往往会发生图像失真，使所得图像与原图像有某种程度上的差别。在许多情况下，人们难以确切了解引起图像降质的具体物理过程及

其数学模型，但却能估计出使图像降质的一些可能原因，针对这些原因采取简单易行的方法，改善图像质量。图像增强一般不能增加原图像信息，只能针对一些成像条件，把弱信号突出出来，使一些信息更容易分辨。图像增强的方法分为频域法和空域法，空域法主要是对图像中的各像素点进行操作；而频域法是在图像的某个变换域内，修改变换后的系数，例如傅立叶变换、DCT 变换等的系数，对

图像进行操作，然后再进行反变换得到处理后的图像。

    MATLAB矩阵实验室（Matrix Laboratory）的简称，具有方便的数据可视化功能，可用于科学计算和工程绘图。它不仅在一般数据可视化软件都具有的功能方面更加完善，而且对于一些其他软件所没有的功能（例如图形的光照处理、色度处理以及四维数据的表现等），MATLAB同样表现了出色的处理能力。它具有功能丰富的工具箱，不但能够进行信号处理、语音处理、数值运算，而且能够完成各种图像处理功能。本文利用MATLAB工具来研究图像频域增强技术。图像增强是为了获得更好质量的图像，通过各种方法对图像进行处理，例如图像边缘检测、分割以及特征提取等技术。图像增强的方法有频域处理法与空域处理法，本文主要研究了频域处理方法中的滤波技术。从低通滤波、高通滤波、同态滤波三个方面比较了图像增强的效果。文章首先分析了它们的原理，然后通过MATLAB软件分别用这三种方法对图像进行处理，处理后使图像的对比度得到了明显的改善，增强了图像的视觉效果。

2.2  频域增强定义和步骤

    图像增强技术基本上可分成两大类：频域处理法和空域处理法。频域处理法[1]的基础是卷积定理，它采用修改图像傅立叶变换的方法实现对图像的增强处理。在频域空间，图像的信息表现为不同频率分量的组合。如果能让某个范围内的分量或某些频率的分量受到抑制而让其他分量不受影响，就可以改变输出图的频率分布，达到不同的增强目的。

频域增强是利用图像变换方法将原来的图像空间中的图像以某种形式转换到其它空间中，然后利用该空间的特有性质方便地进行图像处理，最后再转换回原来的图像空间中，从而得到处理后的图像。

频域增强的主要步骤是：

(1) 选择变换方法，将输入图像变换到频域空间；

(2) 在频域空间中，根据处理目的设计一个转移函数并进行处理；

(3) 将所得结果用反变换得到图像增强。

卷积理论是频域技术的基础。设函数f（x,y）与线性位不变算子h（x,y）的卷积结果是g（x,y），即g(x,y)=h(x,y)*f(x,y)

那么根据卷积定理在频域有：

              G(x,y)=H(u,v)F(u,v)

其中G(x,y)、 H(u,v)、F(u,v)分别是g(x,y)、h(x,y)、f(x,y)的傅立叶变换。

（4）技术所需增强图的傅立叶变换。

（5）将其与一个（根据需要设计的）转移函数相乘。

（6）再将结果进行傅立叶反变换以得到增强的图。

（7）将图像从空域转换到频域所需的变换及将图像从频域空间转换回空域

所需的变换。

（8）在频域空间对图像进行增强加工操作。

常用的频域增强方法有低通滤波和高通滤波。以下分别介绍在MATLAB中如何实现。

同态滤波

一般来说，图像的边缘和噪声都对应于傅立叶变换的高频分量。而低频分量主要决定图像在平滑区域中总体灰度级的显示，故被低通滤波的图像比原图像少一些尖锐的细节部分。同样，被高通滤波的图像在图像的平滑区域中将减少一些灰度级的变化并突出细节部分。为了增强图像细节的同时尽量保留图像的低频分量，使用同态滤波方法 可以保留图像原貌的同时，对图像细节增强.。滤波后，如图（2）

 

 

 

 

 

图1同态滤波过程

 

 

 

 

图2 同态滤波器应用实例              

 

 

同态滤波函数的确定：

以Rh 代表高频增益, Rl 代表低频增益, D( u,v ) 表示频率( u, v) 距滤波器中心( u0, v 0) 的离。传统的同态滤波函数如图2 所示。当Rh> 1, Rl> 1 时,该滤波函数能同时抑制照明分量和增强反射分量,从而满足动态范围压缩和对比度增强两种效果要求。处理目的不同, 可构造不同的滤波器。频域内经常使用的高通滤波器为高斯型高通滤波器, 滤波函数为：

H ( u, v) = 1- ex p[ - D( u, v ) / 2D0^2n]

增强处理。对高斯型高通滤波器稍加修改, 可得以下高斯型高通滤波函数:

H ( u, v) = ( Rh- R l) [ 1- e- c( D (u ,v ) / D0) 2n] + Rl

 

D( u, v) = [ ( u- M/ 2)^ 2+ ( v- N / 2)^2]^1/2

式中: D0 是u0 和v 0 为0 时的D( u, v ) 值, 表示截止频率。对于一幅M×N 的图像, 傅里叶变换后的中心在( M/ 2, N / 2) 式需做平移处理。传统的巴特沃思高通滤波器与同态滤波的传递函数十分相似, 巴特沃思高通滤波的传

递函数为

H ( u, v) = 1/ ( 1+ D0 / D( u, v) )^ 2n

根据两者之间的相似性, 将高通滤波函数稍作修改即可得到对应的巴特沃思高通滤波函数:

H ( u, v) = ( Rh- R l) / ( 1+ cD 0/ D( u, v ) )^2n+ Rl

频域增强算法的实现及代码

4.1  理想低通滤波器

   本次设计是用低通滤波为例，图像中的边缘和噪声都对应图像傅立叶变换中的高频部分，所以如要在频域中消弱其影响就要设法减弱这部分频率的分量。根据要求我们需要选择1个合适的H(u,v)以得到消弱F(u,v)高频分量的G(u,v).在以下讨论中我们考虑对F(u,v)的实部和虚部影响完全相同的滤波转移函数。具有这种特性的滤波器称为零相移滤波器。理想是指小于D0的频率可以完全不受影响地通过滤波器，而大于D0的频率则完全通不过。1个2-D理想低通滤波器的转移函数满足下列条件：

 

\* MERGEFORMAT

 

                                                       

 

(4-1)

 

上式中D0是1个非负整数。D(u,v)是从点（u,v）到频率平面原点的距离，D(u,v)=(u2+v2)1/2。

 

图1给出H的1个剖面图（设D对原点对称），这里理想是指小于D0的频率可以完全不受影响地通过滤波器，而大于D0的频率则完全通不过。因此D0也叫截断频率。尽管理想低通滤波器在数学上定义得很清楚，在计算机模拟中也可实现，但在截断频率处直上直下的理想低通滤波器是不能用实际的电子器件实现的。

                                                                   

                                                                    

                                                     

                                                           

 

                 

 

 

        

 

 图1 理想低通滤波器转移函数的剖面图

     

      如果使用这些“非物理”的理想滤波器，其输出图像会变得模糊和有“振铃（ring）”现像出现。我们可借助卷积定理解释如下。

为简便，考虑1-D的情况。对1个理想低通滤波器，其h(x)的一般形式可由求式（1）的傅立叶反变换得到，其曲线可见图2（a）。现设f(x)是1副只有1个亮像素的简单图像，见图2（b）。这个亮点可看作是1个脉冲的近似。在这种情况下，f(x)和h(x)的卷积实际上是把h(x)复制到f(x)中亮点的位置。比较图2（b）和图2（c）可明显看出卷积使原来清晰的点被模糊函数模糊了。对更为复杂的原始图，如我们认为其中每个灰度值不为零的点都可以看作是1个其值正比于该点灰度值的1个亮点，则上述结论仍可成立。

 

                       图2空间模糊示意图

由图2还可以看出h(x,y)在2-D图像平面上将显示出一系列同心圆环。如对1个理想低通滤波器的H(u,v)求反变换，则可知道h(x,y)中同心圆环的半径是反比于D0的值的。所以如果D0较小，就会使h(x,y)产生数量较少但较宽的同心圆环，并使g(x,y)模糊得比较厉害。当增加D0时，就会使h(x,y)产生数量较多但较窄的同心圆环，并使g(x,y)模糊得比较少。如果D0超出F(u,v)的定义域，则h(x,y)在其对应的空间区域为1，h(x,y)与f(x,y)的卷积仍是f(x,y)，这相

当于没有滤波。

程序代码如下：

 

I1=imread('C:\MATLAB7\bin\1.jpg');

figure,imshow(I1)

I2=imnoise(I1,'salt');

figure,imshow(I2)

f=double(I2);

k=fft2(f);

g=fftshift(k);

[N1,N2]=size(g);

n=2;

d0=50;

n1=round(N1/2);

n2=round(N2/2);

for i=1:N1

    for j=1:N2

        d=sqrt((i-n1)^2+(j-n2)^2);

if d<=d0 h=1;else h=0;

end

    y(i,j)=h*g(i,j);

  end

end

y=ifftshift(y);

m=ifft2(y);

n=uint8(real(m));

figure,imshow(n)

 

  

 

 

 

 

                        

 

 

 

                      原图

 

 

 

 

 

                 加噪后的图像

 

 

 

                            去噪后的图像

 

由实验结果图可以看出加噪图像是使原始图像按照指定的噪声参数加入噪声，经过低通滤波后，去噪图像的椒盐噪声被模糊处理，产生模糊和振铃现象，此振铃现象会随着截止频率的不同而变化。同时人的图像信息也被模糊化，因而效果并不是很好。

4.2   巴特沃斯低通滤波器

    物理上可以实现的一种低通滤波器是巴特沃斯（Butterworth）低通滤波器。在进行图像处理的过程中，获取原始图像后，首先需要对图像进行图像预处理，因为在获取图像的过程中，往往会发生图像失真，使所得图像与原图像有某种程度上的差别。在许多情况下，人们难以确切了解引起图像降质的具体物理过程及其数学模型，但却能估计出使图像降质的一些可能原因，针对这些原因采取简单易行的方法，改善图像质量。由于噪声、光照等原因，使图像质量不高，为了改善视觉效果或便于人、机器对图像的分析理解，一般都需要对图像进行增强处理，但这个过程并没有统一的标准。图像增强一般不能增加原图像信息，只能针对一些成像条件，把弱信号突出出来，使一些信息更容易分辨。 图像增强的方法比较多，可以大概分为对比度增强，直方图增强、平滑和锐化［1］4大类，其中，直方图均衡是图像增强的经典方法，因为其有效性和简单易用性已成为图像增强最常用的方法，他又分为全局均衡和局部均衡2种。全局的直方图均衡［2.3］是对整幅图像进行均衡，使其灰度分布均匀，让每一个灰度等级上的像素个数基本相等，算法简单、计算量小、容易实现，但对图像细节部分增强不够；局部直方图均衡［4.5］则可以增强图像内部细节信息，得到很好的增强效果。Yin［6］通过对小波分解各个分量进行直方图均衡，然后重构得到处理后图像，S．M．Pi-zer［2］提出自适应直方图均衡算法，这也是一种局部均衡算法。在对全局直方图均衡和局部直方图均衡详细分析的基础上，本文提出了一种基于Buterworth低通滤波的图像增强方法。由于Buterworth低通滤波器在抑制噪声的同时，图像边缘模糊程度大大减小，且没有振铃效应。基于以上特点，用Buterworth低通滤波器将低频分量和高频分量分离，低频分量进行均衡后，再将两部分融合，实现图像的增强。

     一个阶为n，截断频率为D0的巴特沃斯低通滤波器的转移函数为

\* MERGEFORMAT  

                                                                        (4-2)

阶为1的巴特沃斯低通滤波器剖面示意图见图3。由图可见低通巴特沃斯滤波器在高低频率间的过渡比较光滑，所以用巴特沃斯滤波器得到的输出图其振铃效应不明显。

一般情况下，常取是H最大值降到某个百分比的频率为截止频率。在上面式中，当D(u,v)=D0时，H(u,v)=0.5(即降到50%)。另一个常用的截止频率值是使H降到最大值的1/21/2时的频率。                          

                      图3 巴特沃斯低通滤波器转移函数的剖面示意图

 

  

用MATLAB实现Butterworth低通滤波器的代码所示：

clear all;

I1=imread('C:\MATLAB7\work\2.jpg');

figure,imshow(I1);

f=double(I1);

k=fft2(f);

g=fftshift(k);

[N1,N2]=size(g);

n=2;

d0=50;

n1=round(N1/2);

n2=round(N2/2);

for i=1:N1

    for j=1:N2

        d=sqrt((i-n1)^2+(j-n2)^2)

        h=1/(1+0.414*(d/d0)^(2*n));

        y(i,j)=h*g(i,j);

    end

end

y=ifftshift(y);

X2=ifft2(y);

X3=uint8(real(X2));

figure,imshow(X3);

 

由实验结果图可以看出加噪图像，经过低通滤波后，去噪图像被模糊处理，产生模糊和振铃现象，此振铃现象会随着截止频率的不同而变化。同时人的图像信息也被模糊化，因而效果并不是很好。  

MATLAB实现Butterworth高通滤波器代码所示：

I1=imread('C:\MATLAB7\bin\che.jpg');

figure,imshow(I1)

f=double(I1);

k=fft2(f);

g=fftshift(k);

[N1,N2]=size(g);

n=2;

d0=25;

n1=fix(N1/2);

n2=fix(N2/2);

for i=1:N1

    for j=1:N2

        d=sqrt((i-n1)^2+(j-n2)^2);

        if d==0

            h=0;

        else

           h=1/(1+(d0/d)^(2*n));

       end

    y(i,j)=h*g(i,j);

  end

end

y=ifftshift(y);

X2=ifft2(y);

X3=uint8(real(X2));

figure，imshow(X3)；

 

 

 

 

 

 

 

 

                原图

 

 

 

 

 

 

 

 

               处理后的图像