PyTorch深度学习-03梯度下降(快速入门)
目录
- 1.Gradient Descent (梯度下降)
-
- 1.1 Optimization Problem (优化问题)
- 1.2 Gradient Descent algorithm (梯度下降算法)
-
- 1.2.1 Gradient (梯度)
- 1.2.2 Update (更新权重)
- 1.3 代码实现
- 1.4 结果截图
- 2.Stochastic Gradient Descent (随机梯度下降)
-
- 2.1 代码实现
- 2.2 结果截图
- 3.Batch (批量的随机梯度下降)
1.Gradient Descent (梯度下降)
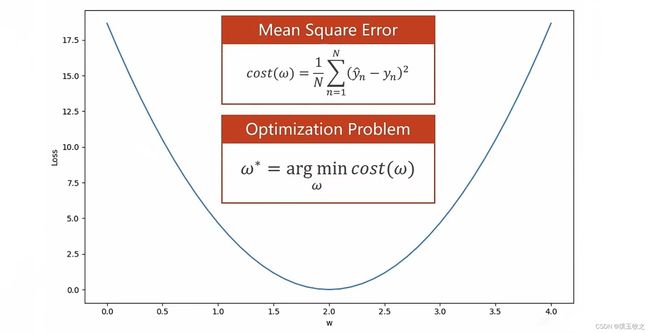
1.1 Optimization Problem (优化问题)
1.2 Gradient Descent algorithm (梯度下降算法)
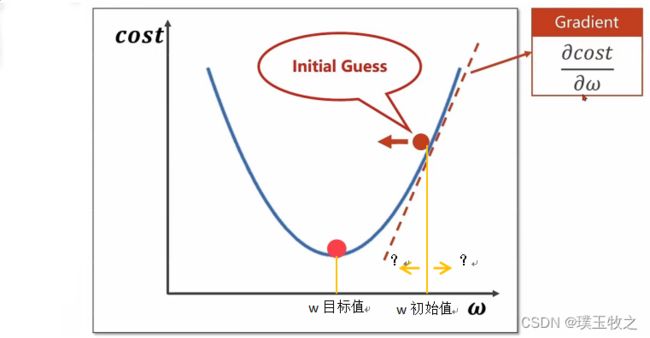
1.2.1 Gradient (梯度)
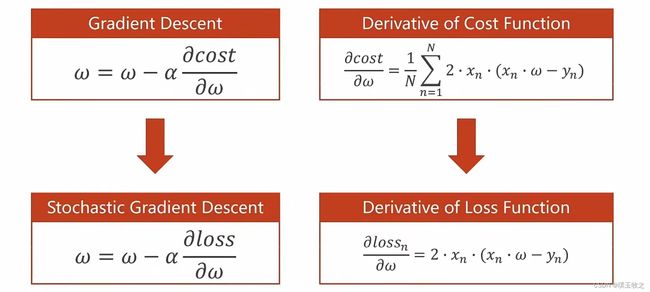
用目标函数对权重求导,就可以得到它的上升方向。负导数为下降方向。
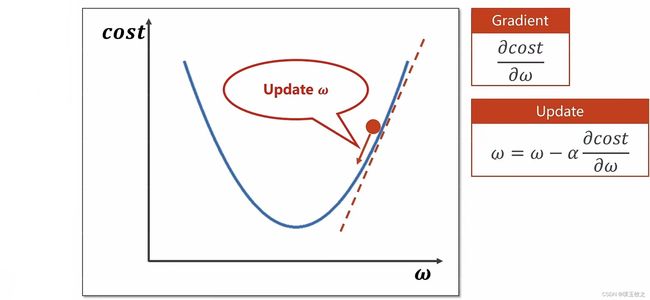
1.2.2 Update (更新权重)
权重减学习率乘导数
-
贪心算法:每次迭代都朝着下降最快的方向走一步,梯度下降不一定能得到最优结果,但能得到在局部区域的最优结果。
-
鞍点:在鞍点处梯度等于0,即g=0,所以在鞍点处,据 w=w-ag,可知a*g=0,则无论步长值是多少,w值都无法再次改变。


1.3 代码实现
import matplotlib.pyplot as plt
x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0] #输入训练集数据
loss_list = []
Epoch_list = []
w = 1.0 #猜测一个初始权重
def forward(x): #定义前馈计算
return x * w #y_hat=x*w
def cost(xs, ys): #计算MSE的目标函数
cost = 0
for x, y in zip(xs, ys): #zip拼装
y_pred = forward(x) #计算y_hat=x*w
cost += (y_pred - y) ** 2 #计算(y_hat-y)的平方,再累加
return cost / len(xs) #除样本数量=均值
def gradient(xs, ys): #求梯度函数
grad = 0
for x, y in zip(xs, ys):
grad += 2 * x * (x * w - y)
return grad / len(xs)
print('Predict (before training)', 4, forward(4))
for epoch in range(100): #进行100轮训练
cost_val = cost(x_data, y_data)
grad_val = gradient(x_data, y_data) #求梯度
w -= 0.01 * grad_val #更新
print('Epoch:', epoch, 'w=', w, 'loss=', cost_val) #输出训练日志,Epoch:训练轮数
loss_list.append(cost_val)
Epoch_list.append(epoch)
print('Predict (after training)', 4, forward(4))
#Draw the grap
plt.plot(Epoch_list, loss_list)
plt.ylabel('Loss')
plt.xlabel('Epoch')
plt.show()
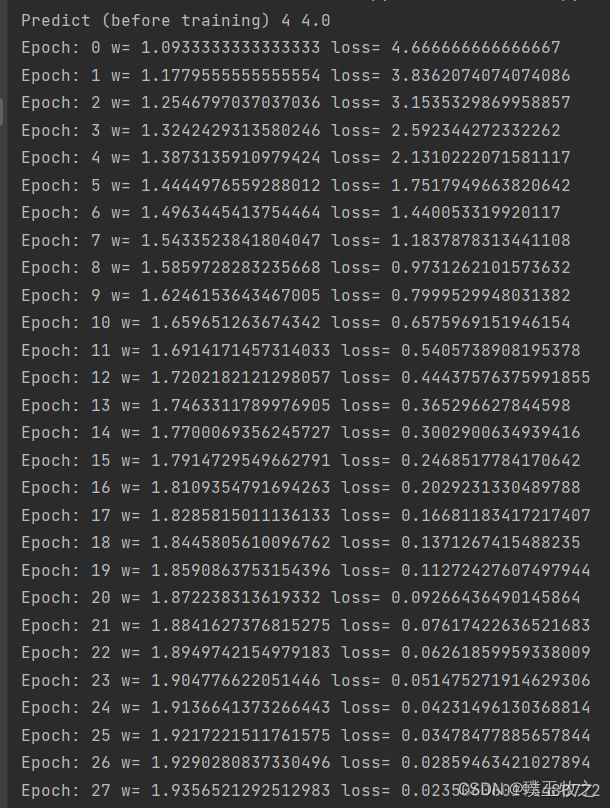
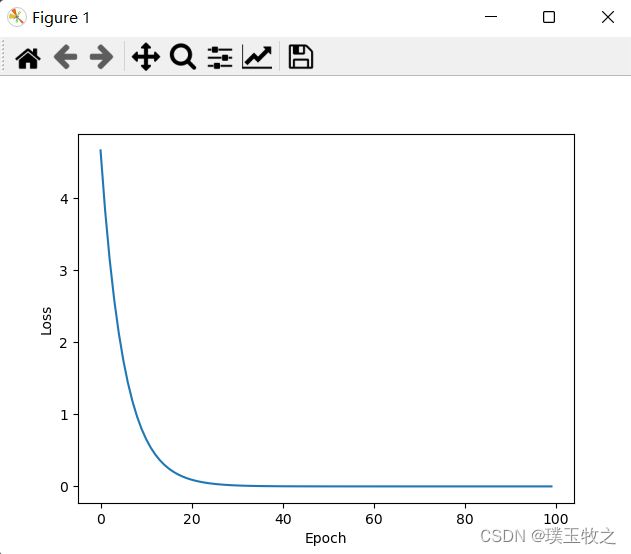
1.4 结果截图
2.Stochastic Gradient Descent (随机梯度下降)
由于损失函数可能是带有鞍点的,到达鞍点后就无法继续向前走了。我们拿到的数据总是有噪声的,在陷入鞍点时,随机噪声可能会把我们向前推动。
梯度下降是用所有样本的平均损失作为梯度下降的更新依据,随机梯度下降是一共提供N个数据,从里面随机选一个,公式就变成了拿单个样本的损失函数对权重求导。
2.1 代码实现
import matplotlib.pyplot as plt
x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0] #输入训练集数据
w = 1.0
def forward(x): #定义前馈计算
return x * w
def loss(x, y):
y_pred = forward(x) # 计算y_hat=x*w
return (y_pred - y) ** 2 #计算y_hat-y的平方
def gradient(x, y): #求梯度函数
return 2 * x * (x * w - y)
epoch_list = []
loss_list = []
print('Predict (before training)', 4, forward(4))
for epoch in range(100):
for x, y in zip(x_data, y_data):
grad = gradient(x, y) #对每个样本求梯度
w = w - 0.01 * grad #拿一个样本然后就进行更新权重
print("\tgrad: ", x, y, grad)
l = loss(x, y)
print("progress:", epoch, "w=", w, "loss=", 1)
epoch_list.append(epoch)
loss_list.append(l)
print('Predict (after training)', 4, forward(4))
#Draw the grap
plt.plot(epoch_list, loss_list)
plt.ylabel('loss')
plt.xlabel('epoch')
plt.show()
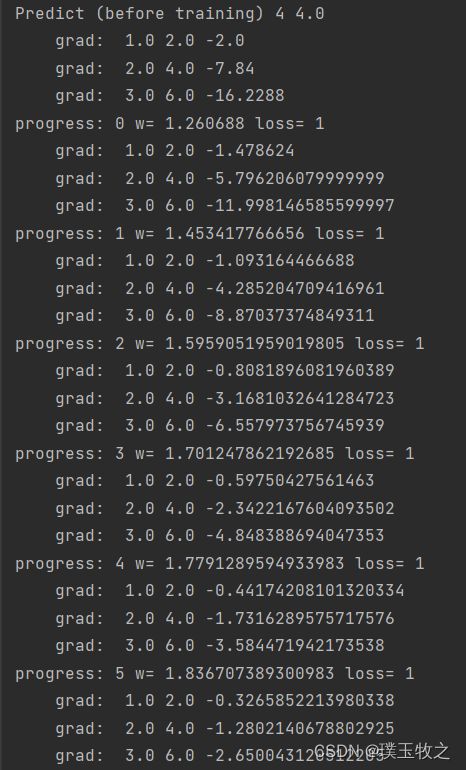
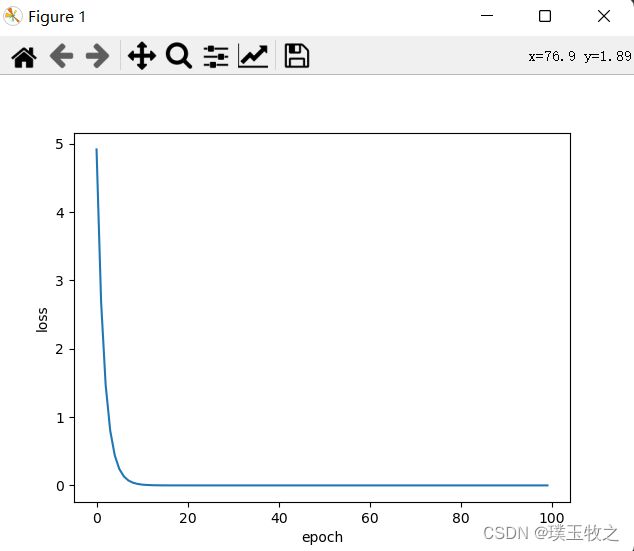
2.2 结果截图
3.Batch (批量的随机梯度下降)
- 梯度下降的计算是并行的,随机梯度下降的两个样本之间是有依赖的,不能并行。所以,梯度下降法效率最高,随机梯度下降的性能较好,但时间复杂度高。
- 因此在深度学习中,会利用一种折中方式——Batch,批量的随机梯度下降(若干个样本一组,每次用一组样本求相应梯度,然后进行更新)
- 在深度学习中默认采用的随机梯度下降sdd算法用的就是batch方法。
本文参考:《PyTorch深度学习实践》