机器学习概论 聚类算法实现(实验四)

一、实验目的
1、熟悉使用numpy模块生成二维正态分布；
2、掌握kmeans聚类的代码实现；
3、熟悉numpy的使用；
4、熟悉matplotlib的使用。
二、实验设备
计算机：CPU四核i7 6700处理器；内存8G； SATA硬盘2TB硬盘； Intel芯片主板；集成声卡、千兆网卡、显卡； 20寸液晶显示器。
编译环境：python解释器、Pycharm编辑器
三、实验内容
1、新建项目和文件，并导入numpy和matplotlib
（1）打开Pycharm，新建项目，并在该项目下新建文件kmeans_clustering.py。
（2）导入一些编程中需要的包。

import numpy as np
import matplotlib.pyplot as plt
2、构造一个函数data_producer
（1）定义函数头data_producer，该函数有三个参数，miu，sigma，sample_no分别表示生成二维正态分布的均值，标准差和生成样本点的个数。
（2）调用numpy.random.multivariate_normal生成二维正态分布的数据。
（3）该函数返回生成的数据。```

```java

def data_producer(miu, sigma, sample_no):
    data = np.random.multivariate_normal(miu, sigma, sample_no)
    return data
``3、编写一个类KmeansClustering
（1）构造一个类KmeansClustering，并定义构造函数，需要数据集和kmeans算法中的k作为输入。
（2）定义类方法cluster，实现kmeans算法，并打印分类后的混淆矩阵，返回分类后的数据。`

```java
class KmeansClustering:
    def __init__(self, data, k, maxrenew):
        self.data = data
        self.k = k
        self.Sigma1 = None
        self.Sigma2 = None
        self.Sigma3 = None
        self.renew = 0
        self.maxrenew = maxrenew
    def cluster(self):
        a = []; iter = 0
        for i in range(self.k):
            x = np.random.randint(0, np.shape(self.data)[0])
            a.append(self.data[x])
        c = np.array(a)
        Old_d = np.copy(c)
        while(self.maxrenew <=1000):
            New_d = np.copy(Old_d)
            self.Sigma1 = []
            self.Sigma2 = []
            self.Sigma3 = []
            for j in range(np.shape(self.data)[0]):
                if np.argmin(np.sqrt(np.sum((self.data[j, :-1]-New_d[:, :-1])**2, axis=1))) == 0:
                    self.Sigma1.append(self.data[j])
                if np.argmin(np.sqrt(np.sum((self.data[j, :-1]-New_d[:, :-1])**2, axis=1))) == 1:
                    self.Sigma2.append(self.data[j])
                if np.argmin(np.sqrt(np.sum((self.data[j, :-1]-New_d[:, :-1])**2, axis=1))) == 2:
                    self.Sigma3.append(self.data[j])
            self.data=np.vstack((self.Sigma1, self.Sigma2, self.Sigma3))
            aa = np.shape(self.Sigma1)[0]
            bb = np.shape(self.Sigma2)[0]
            cc = np.shape(self.Sigma3)[0]
            qq = np.shape(self.data[aa+1:bb+1])
            New_d[0] = np.array(np.mean(self.data[:aa+1], axis=0))
            New_d[1] = np.array(np.mean(self.data[aa+1:aa+bb+1], axis=0))
            New_d[2] = np.array(np.mean(self.data[aa+bb+1:], axis=0))
            if np.sum(New_d != Old_d) == 0:
                self.renew += 1
                print("更新不变的次数", self.renew)
                if self.renew >= 3:
                    return self.Sigma1, self.Sigma2, self.Sigma3
            else:
                iter += 1
                print("迭代次数", iter)
                Old_d = New_d
        return self.Sigma1, self.Sigma2, self.Sigma3

4、编写if name”main”:
（1）构造if name”main”:。
（2）在其中设置生成二维正态分布的参数，调用data_producer获取数据。
（3）初始化KmeansClustering类的一个对象my_kmeans，调用cluster方法。
（4）绘制原始数据分布和分类后的数据分布。

if __name__ == "__main__":
    Sample_No = 100
    Miu1 = [0, 3]
    Sigma_1 = np.array([[2, 0], [0, 2]])
    Miu2 = [3, 0]
    Sigma_2 = np.array([[2, 0], [0, 2]])
    Miu3 = [5, 5]
    Sigma_3 = np.array([[2, 0], [0, 2]])
    Data1 = data_producer(Miu1, Sigma_1, Sample_No)
    Data1 = np.hstack((Data1, np.zeros([Sample_No, 1], dtype=np.int8)))
    Data2 = data_producer(Miu2, Sigma_2, Sample_No)
    Data2 = np.hstack((Data2, np.zeros([Sample_No, 1], dtype=np.int8)))
    Data3 = data_producer(Miu3, Sigma_3, Sample_No)
    Data3 = np.hstack((Data3, np.zeros([Sample_No, 1], dtype=np.int8)))
    Data = np.vstack([Data1, Data2, Data3])
    my_kmeans = KmeansClustering(Data, 3, 1000)
    Sigma_1, Sigma_2, Sigma_3 = my_kmeans.cluster()
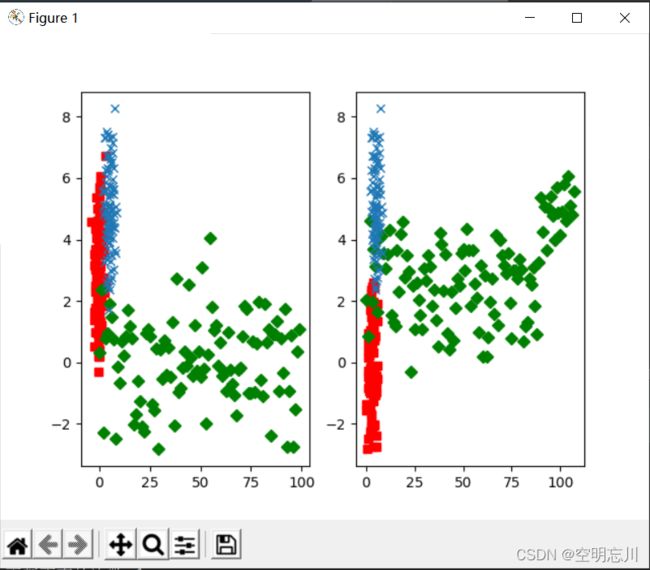
    plt.figure()
    plt.subplot(121)
    plt.plot(Data1[:, 0], Data1[:, 1], 'rs', Data2[:, 1], 'gD', Data3[:, 0], Data3[:, 1], "x")
    plt.subplot(122)
    plt.plot(np.array(Sigma_1)[:, 0], np.array(Sigma_1)[:, 1], 'rs', np.array(Sigma_2)[:, 1],
             'gD', np.array(Sigma_3)[:, 0], np.array(Sigma_3)[:, 1], "x")
    plt.show()

实验截图：

五、实验总结
本次实验学习了kmeans聚类的代码实现，一种无监督的聚类算法。在给定的样本集，按照样本之间的距离大小，将样本集划分为K个簇。但是从几组数据来看，迭代次数的多样性，对于K值的选取不好把握，如果数据不平衡，则kmeans聚类效果会不佳。