【PyTorch深度学习实践】深度学习之线性模型和梯度下降算法
文章目录
- 前言
- 一、线性模型
- 二、梯度下降法
- 总结
前言
在学习深度学习过程中,我们需要知道一个基本的流程,首先需要准备数据集(Dataset),然后选择模型(Model),再用该模型进行训练(Training),最后将训练后的模型用于推理(Inferring)。
本章中我们先从最简单的线性模型和梯度下降算法讲起。
一、线性模型
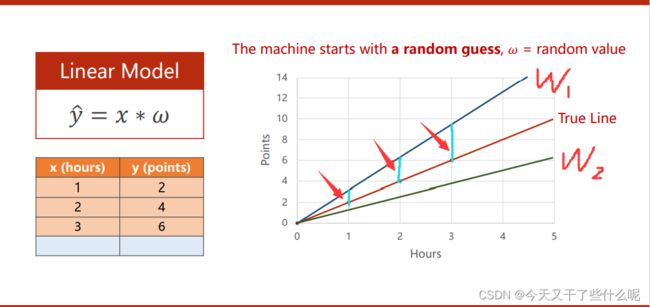
这里我们以一个最简单的线性模型为例
y=w*x ,x为输入值,y为实际值
w为权重,图中给了三个样本值,(1,2),(2,4),(3,6),因为只是基础入门用,所以数据没选那么多
假设我们的样本是可以用线性模型表示出来的,那么我们在训练模型的过程中就是为了去找到一个合适的权重w1使这个模型能表示我们的这些样本值(这里是因为数据量小,我们可以一眼看出权重为2,如果在大量的数据面前,我们肯定需要选择合适的方法去找到这个权重)
如下图,在这里我们使用穷举法,通过枚举w来验证这个权重是否能符合这个模型,红色箭头所指的地方是用来判断我们的模型与实际的样本之间的差值
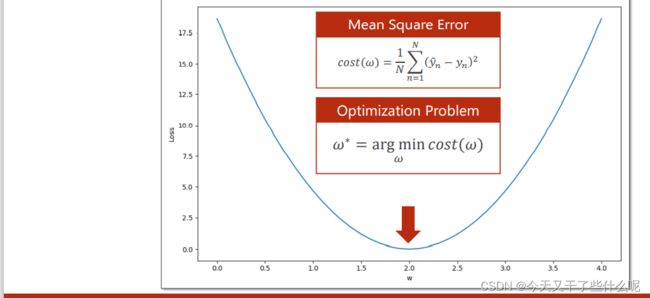
我们将这个差值的平方定义为损失值loss,所有样本差值的平方和取平均定义为平均平方误差MSE
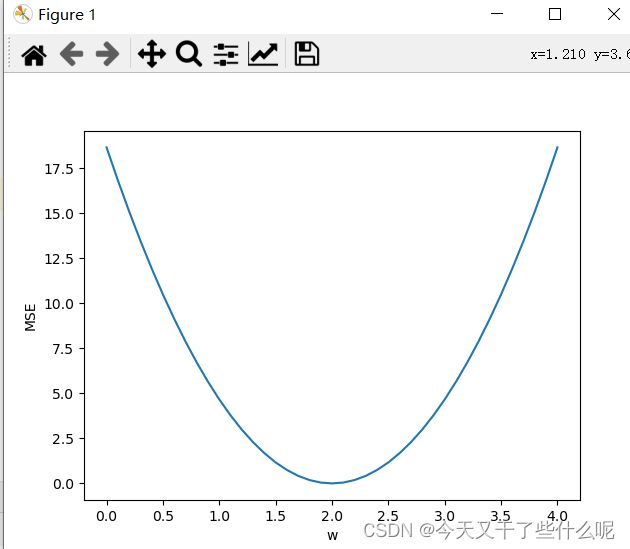
判断我们穷举的权重w是否能较为准确的描述该模型,就是要让算出来的平均平方误差MSE越小即可。下面的图便是权重w和平均平方误差MSE的关系,这个图比较直观,可以看出在w=2时MSE的值最小
以下给出训练代码
import numpy as np
import matplotlib.pyplot as plt #绘图所用的包
x_data=[1.0,2.0,3.0] #数据集
y_data=[2.0,4.0,6.0]
def forward(x): #线性函数
return x * w
def loss(x,y): #计算损失loss
y_pred=forward(x)
return (y_pred-y) * (y_pred-y)
w_list=[]
mse_list=[]
for w in np.arange(0.0, 4.1, 0.1): #在0到4之间,步长为0.1,枚举权重w
print('w',w)
l_sum=0
for x_val,y_val in zip(x_data,y_data):
y_pred_val=forward(x_val)
loss_val=loss(x_val,y_val)
l_sum+=loss_val #差值平方和
print('\t',x_val,y_val,y_pred_val,loss_val)
print("MSE=",l_sum/3) #平均平方误差
w_list.append(w)
mse_list.append(l_sum/3)
plt.plot(w_list,mse_list)
plt.ylabel('MSE')
plt.xlabel('w')
plt.show()
二、梯度下降法
当数据量大的时候,权重多的时候,我们是无法像上面一样在0到4之间通过枚举的方式寻找适合模型的权重w,因为那样会花费很多时间,所以我们在这一节选择用梯度下降法来更新训练时的权重
至于梯度是什么,高等数学里面讲得很详细,这里就不再叙述,将平均平方误差MSE对权重w求导就是梯度,我们每次选择梯度下降的方向来更新权重w,更新公式如下:
沿梯度下降方向更新w很好理解,对于这样的凸函数来说,沿梯度下降方向更新最终w会在最下面收敛,这时也正好对应MSE最小,符合我们训练模型的目的。但是梯度下降法也有缺点:
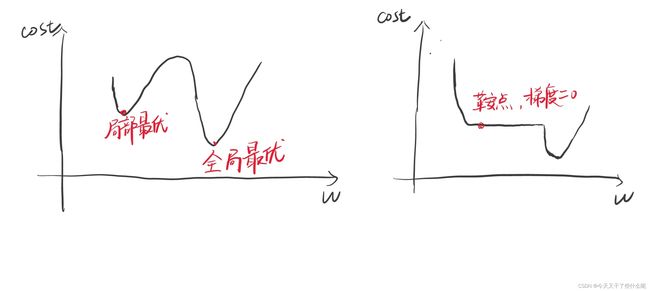
缺点一:当权重w在局部最优点位置变化时,根据w的更新公式,最终w会收敛与局部最优点,而到达不了全局最优点
缺点二:当权重w更新过程中,到达鞍点位置时(没有斜率),根据w的更新公式,w是无法再进行更新导致找不到最优点。
梯度下降法代码如下:
import numpy as np
import matplotlib.pyplot as plt
x_data=[1.0, 2.0, 3.0]
y_data=[2.0, 4.0, 6.0]
loss_list=[]
Epoch_list=[]
w=1.0
def forward(x):
return x*w #线性模型
def cost(xs,ys):
cost=0
for x,y in zip(xs,ys):
y_pred=forward(x)
cost+=(y_pred-y)**2
return cost/len(xs) #平均平方误差MSE
def gradient(xs,ys):
grad=0
for x,y in zip(xs,ys):
grad+=2*x*(x*w-y)
return grad/len(xs) #梯度
print('Predict(before training)',4,forward(4))
for epoch in range(100): #epoch为训练次数,这里设训练100次
cost_val=cost(x_data,y_data)
grad_val=gradient(x_data,y_data)
w-=0.01*grad_val #0.01为学习率,学习率不能设得太大
print('Epoch:',epoch,'w=',w,'loss',cost_val)
loss_list.append(cost_val)
Epoch_list.append(epoch)
print('Predict(after training)',4,forward(4))
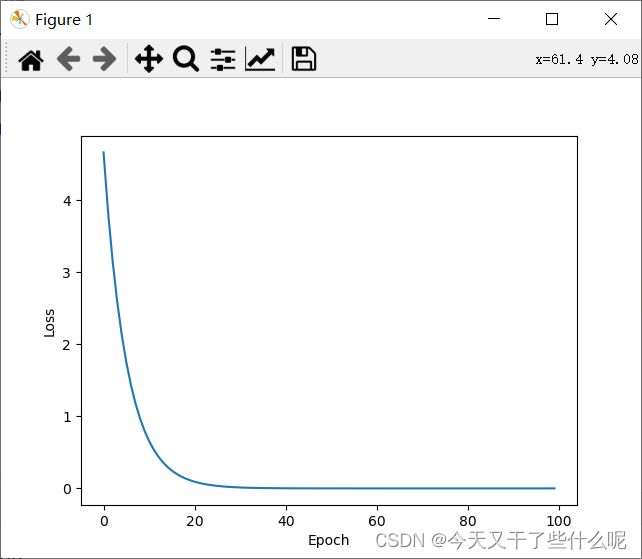
plt.plot(Epoch_list,loss_list)
plt.ylabel('Loss')
plt.xlabel('Epoch')
plt.show()
如下图,大概训练20次左右,损失值趋于0,也就是说训练20次左右的权重w可以大致描述之前给的样本了
总结
本章主要介绍了线性模型和梯度下降法,在线性模型一节中我们介绍的是用穷举法来寻找权重w,而在后一节中我们讲述的是用梯度下降法来寻找权重w。另外,我们讲了深度学习过程的四个基本流程,代码中也有体现,准备数据集,选择模型,训练,推理。