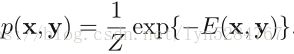机器学习-马尔可夫随机场（MRF）

一，介绍

首先，我们来交接几个基本概念：

1）马尔可夫随机过程：是随机过程的一种，其原始模型为马尔科夫链，其主要特征是：在已知眼下状态（如今）的条件下，它未来的变化（将来）不依赖于以往的变化，而只跟眼下所处的状态有关。

2）随机场：随机场实际上是一种特殊的随机过程，跟普通的随机过程不同的是，其參数取值不再是实数值而有是多维的矢量值甚至是流行空间的点集。

3）马尔可夫随机场：马尔科夫随机场是具有马尔科夫特性的随机场，它每一个结点的取值只与周围结点有关。

4）团：任意的两结点，如果有连接线，称为团。

马尔科夫随机场（MRF）是由变量x1, ..., xn组成的概率分布p，由无向图G定义，其中节点对应于变量xi。 概率p形式为：

                                                                       

其中C表示G的团集合（即完全连通子图）。

                                                                      

是标准化常数，确保整个分布和为一。

一般情况下，为了方便，通常只求对数形式：

                                                               

实例:

假设我们有两张图，第一张为原图，第二章为加入噪声的图：

                                

我们定义：

• yi：噪声图中的像素
• xi：原图中的像素，对应噪声图中的 yi

接着假设，原图中，各像素只与相邻像素相关，那么我们就可以获得一个具有马尔可夫性质的图模型，并且（xi,yi,xj）是一个极大团，接下来就可以用马尔可夫随机场进行处理。

因为我们需要处理的是二值图，首先我们定义 xi ∈ {-1, +1}，假设这里白色为1，黑色为-1。

对于原图像素与噪声图像素构成的团 {xi, yi}，我们定义一项 −ηxiyi，其中 η 为一个非负的权重。当两者同号时，这项的值为−η，异号时为 η。这样，当噪声图像素与原图像素较为接近时，这一项能够降低 energy（因为为负）。

对于噪声图中相邻像素构成的团 {xi, xj}，我们定义一项 −βxixj，其中 β 为一个非负的权重。这样，当处理过的图像里相邻的像素较为接近时，这一项能够降低 energy（因为为负）。

最后，我们再定义一项 hxi，使处理过的图像整体偏向某一个像素值。

对图像中的每一个像素，将这三项加起来，就得到我们的 energy function：

                                                    

对应联合概率：

                                                              

显然 energy 越低，降噪过的图像与原图一致的概率越高。

得到了 energy function 的表示，接下来我们需要做的就是想办法让处理过后的图像具备尽可能低的 energy，从而获得更高的概率 P(X=x)。

注意如果我们固定 y 作为先验知识（假设噪声图不变），我们所求的概率就变成了 p(x|y)，这种模型叫做 Ising Model，在统计物理中有广泛的应用。这样我们的问题就成了以 y 为基准，想办法不断变动 x，然后找出最接近原图的 x。

一种最简单的办法是我们先将 x 初始化为 y，然后遍历每一个元素，对每个元素分别尝试 1 和 -1 两种状态，选择能够得到更小的 energy 的那个，实际上相当于一种贪心的策略，这种方法称为 Iterated Conditional Modes（ICM）。

另外，也可以尝试使用模拟退火（Simulated annealing）或者爬山算法等，在有限的时间内找到尽可能好的解。

模拟退火算法流程如下：

                        1，创建一个随机解；

                        2，创建一个随机跳跃值及跳跃方向；

                        3，新解优于之前则替换，或者新解比之前要差，但是公式P值足够大，也进行替换（可能下次可以找到更优的                             解）：

                       

                       其中，newcost为新解，nowcost为之前的解，T为初始温度，一般初始值需要足够大。

                       4，如果有进行降温计算，则需要更新T值：T=r*T，r为设定的降温率(取值在0-1之间)，r约接近1，则降温慢，找 到最优解的概率高，但花费时间长。

                       5，单T值小于开始设定的的大小后，算法结束。

python代码：

创建了两个py文件：denoise.py、util.py

denoise.py代码：

from random import random
import time
import os
import argparse

import numpy as np
import matplotlib.pyplot as plt
from PIL import Image

from util import *


def E_generator(beta, eta, h):
    # 求E = h * sum{xi} - beta * sum{xi xj} - eta * sum{xi yi}
    # h=0;eta=0.0021;beta=0.001
    def E(x, y):
        xxm = np.zeros_like(x)
        #sum{xi xj} 需要每个点都乘以它上下左右相邻元素的和
        xxm[:-1, :] = x[1:, :]  # Xi下面的元素构成的矩阵
        xxm[1:, :] += x[:-1, :]  # Xi上面的元素构成的矩阵
        xxm[:, :-1] += x[:, 1:]  # Xi右面的元素构成的矩阵
        xxm[:, 1:] += x[:, :-1]  # Xi左面的元素构成的矩阵
        xx = np.sum(xxm * x)  # 计算sum{xi xj}
        xy = np.sum(x * y)    # 计算sum{xi yi}
        xsum = np.sum(x)      # 计算sum{xi}
        return h * xsum - beta * xx - eta * xy

    def is_valid(i, j, shape):
        """Check if coordinate i, j is valid in shape."""
        return i >= 0 and j >= 0 and i < shape[0] and j < shape[1]

    # 将矩阵中一个值取反，并计算新的energy
    # E1--当前energy；i，j矩阵元素位置，x--原图像素矩阵，y--噪声图像素矩阵
    def localized_E(E1, i, j, x, y):
        oldval = x[i, j]
        newval = oldval * -1  # 将状态取反
        # 计算新的energy，需要先减去原元素值，再加上现元素值
        E2 = E1 - (h * oldval) + (h * newval)
        E2 = E2 + (eta * y[i, j] * oldval) - (eta * y[i, j] * newval)
        adjacent = [(0, 1), (0, -1), (1, 0), (-1, 0)]
        neighbors = [x[i + di, j + dj] for di, dj in adjacent
                     if is_valid(i + di, j + dj, x.shape)]
        E2 = E2 + beta * sum(a * oldval for a in neighbors)
        E2 = E2 - beta * sum(a * newval for a in neighbors)
        return oldval, newval, E1, E2

    return E, localized_E

# 模拟退火算法当前温度
def temperature(k, kmax):
    return 1.0 / 500 * (1.0 / k - 1.0 / kmax)

# 如果E1大，进行替换，否则用模拟退火公式计算P值
def prob(E1, E2, t):
    return 1 if E1 > E2 else np.exp((E1 - E2) / t)

# 模拟退火算法，y--噪声图像矩阵，E--energy计算公式，localized_E--计算函数，temp_dir--路径
def simulated_annealing(y, kmax, E, localized_E, temp_dir):
    x = np.array(y)         #将x初始化为y
    Ebest = Ecur = E(x, y)  # 获取初始energy
    initial_time = time.time()  # 获取当前时间戳
    energy_record = [[0.0, ], [Ebest, ]]

    for k in range(1, kmax + 1):
        start_time = time.time()
        t = temperature(k, kmax + 1)
        print ("k = %d, Temperature = %.4e" % (k, t))
        accept, reject = 0, 0
        for idx in np.ndindex(y.shape):  # 编译矩阵每一个元素，先行后列
            old, new, E1, E2 = localized_E(Ecur, idx[0], idx[1], x, y)
            p, q = prob(E1, E2, t), random()   # 获取p值和一个0-1的随机数判断是否计算
            if p > q:                         # E1大或者模拟退火算法计算的p值大则直接替换
                accept += 1
                Ecur, x[idx] = E2, new
                if (E2 < Ebest):
                    Ebest = E2  # 更新最佳energy
            else:
                reject += 1
                Ecur, x[idx] = E1, old

        end_time = time.time()
        energy_record[0].append(end_time - initial_time)
        energy_record[1].append(Ebest)

        print ("--- k = %d, accept = %d, reject = %d ---" % (k, accept, reject))
        print ("--- k = %d, %.1f seconds ---" % (k, end_time - start_time))

        temp = sign(x, {-1: 0, 1: 255})
        temp_path = os.path.join(temp_dir, 'temp-%d.png' % (k))
        Image.fromarray(temp).convert('1', dither=Image.NONE).save(temp_path)   # 画图
        print ("[Saved]", temp_path)

    return x, energy_record


def ICM(y, E, localized_E):
    """Greedy version of simulated_annealing()."""
    x = np.array(y)
    Ebest = Ecur = E(x, y)  # initial energy
    initial_time = time.time()
    energy_record = [[0.0, ], [Ebest, ]]

    for idx in np.ndindex(y.shape):  # for each pixel in the matrix
        old, new, E1, E2 = localized_E(Ecur, idx[0], idx[1], x, y)
        if (E2 < Ebest):               # 如果E2更小则更新
            Ecur, x[idx] = E2, new
            Ebest = E2
        else:
            Ecur, x[idx] = E1, old

        if idx[1] == y.shape[1] - 1:
            used_time = time.time() - initial_time
            energy_record[0].append(used_time)
            energy_record[1].append(Ebest)

    return x, energy_record

# 图像降噪
def denoise_image(image, args, method='SA'):
    data = sign(image.getdata(), {0: -1, 255: 1})  # 白色映射到 -1, 黑色映射到1
    E, localized_E = E_generator(args.beta, args.eta, args.argh)
    temp_dir = os.path.dirname(os.path.realpath(args.output))
    y = data.reshape(image.size[::-1])  # 获取图像矩阵
    if method == 'SA':
        result, energy_record = simulated_annealing(
            y, args.kmax, E, localized_E, temp_dir)
    else:
        result, energy_record = ICM(y, E, localized_E)
    result = sign(result, {-1: 0, 1: 255})
    output_image = Image.fromarray(result).convert('1', dither=Image.NONE)
    return output_image, energy_record


def main():
    args = get_args(src="flipped.png", dest="best.png")

    # 降噪并保存
    image = Image.open(args.input)
    result, energy_record = denoise_image(image, args, args.method)
    result.save(args.output)
    print ("[Saved]", args.output)

    # plot time-energy relationship and save
    plt.plot(*energy_record)
    plt.xlabel('Time(s)')
    plt.ylabel('Energy')
    output_dir = os.path.dirname(os.path.realpath(args.output))
    plot_path = os.path.join(output_dir, args.method + '-energy-time.png')
    plt.savefig(plot_path)
    print ("[Saved]", plot_path)

if __name__ == "__main__":
    main()

util.py代码：

import os
import argparse

import numpy as np

# 映射函数
def sign(data, translate):
    temp = np.array(data)
    return np.vectorize(lambda x: translate[x])(temp)

# 获取参数
def get_args(src="in.png", dest="flipped.png"):
    # 定义默认参数
    parser = argparse.ArgumentParser()
    parser.add_argument("-i", "--input", type=str, default=src)
    parser.add_argument("-o", "--output", type=str, default=dest)
    parser.add_argument("-d", "--density", type=float, default=0.1)
    parser.add_argument("-b", "--beta", type=float, default=1e-3)
    parser.add_argument("-e", "--eta", type=float, default=2.1e-3)
    parser.add_argument("-a", "--argh", type=float, default=0.0)
    parser.add_argument("-k", "--kmax", type=int, default=15)
    parser.add_argument("-m", "--method", type=str, default='BA')
    args = parser.parse_args()

    file_dir = os.path.dirname(os.path.realpath(__file__))
    parent_dir, _ = os.path.split(file_dir)
    args.input = os.path.join(parent_dir, 'img', args.input)
    args.output = os.path.join(parent_dir, 'img', args.output)
    return args

贪心算法得到结果：

模拟退火算法迭代15次结果：