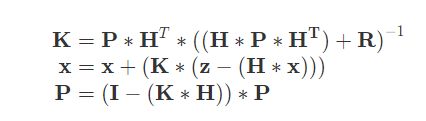车流量统计

使用yolov3模型进行目标检测，然后使用SORT算法进行目标追踪，使用卡尔曼滤波器进行目标位置预测，并利用匈牙利算法对比目标的相似度，完成车辆目标追踪，利用虚拟线圈的思想实现车辆目标的计数，完成车流量的统计。

1.多目标追踪（MOT）

在一段视频中同时跟踪多个目标。多目标跟踪可以看作多变量估计问题。
初始化方法：常见初始化方法DBT和DFT。
DBT:先检测目标，然会将目标关联进入跟踪轨迹中。
DFT：单目标跟踪领域的常见初始化方法，即每当新目标出现时，人为告诉算法新目标的位置。
处理模式：online，offline
online:对视频帧逐帧进行处理，当前帧的跟踪仅利用过去的信息。
offline：会利用前后视频帧的信息对当前帧进行目标跟踪，只适用于视频。
运动模型：
为了简化多目标跟踪的难度，我们引入运动模型类简化求解过程，运动模型捕捉目标的动态行为，它估计目标在未来帧中的潜在位置，从而减少搜索空间。
对于车辆的运动法制可以分为线性和非线性运动。
跟踪方法：基于Kalman和KM算法的后端优化算法
这类算法能达到实时性，但依赖于检测算法效果要好（输出最终结果的好坏依赖于较强的检测算法，而基于卡尔曼加匈牙利匹配的准总算法作用在于能够输出检测目标的id，其次能保证追踪算法的实时性），这样追踪效果会好，id切换少。代表算法是SORT。
SORT是一种实用的多目标跟踪算法，引入线性速度模型与卡尔曼滤波来进行位置预测，在无合适匹配检测框的情况下，使用运动模型来与预测物体的位置。
匈牙利算法是一种寻找二分图的最大匹配的算法，在多目标跟踪问题中可以简单理解为寻找前后两帧的若干目标的匹配最优解的一种算法。而卡尔曼滤波可以看作是一种运动模型，用于对目标的轨迹进行预测，并且使用确信度较高的跟踪结果进行预测结果的修正。
先实现目标检测网络，检测的输出结果主要是将检测框的位置信息输入到多目标追踪算法中。

辅助功能

交并比：
IOU是目标检测中使用的一个概念是产生的候选框与原标记框的交叠率。
在多目标跟踪中，用来判别跟踪框核目标检测框之间的相似度。

def iou(bb_test,bb_gt):
	xx1=np.maximum(bb_test[0],bb_gt[0])
	yy1=np.maximum(bb_test[1],bb_gt[1])
	xx2=np.minimum(bb_test[2],bb_gt[2])
	yy2=np.minimum(bb_test[3],bb_gt[3])
	w=np.maximum(0.,xx2-xx1)
	h=np.maximum(0,yy2-yy1)
	wh=w*h
	o=wh/((bb_test[2]-bb_test[0])*(bb_test[3]-bb_test[1])+(bb_gt[2]-bb_gt[0])*(bb_gt[3]-bb_gt[1])-wh)
	return o

候选框的表现形式
一种是左上角坐标核右下角坐标
[x,y,s,r]表示中心点坐标，s是面积尺度，r是纵横比，卡尔曼滤波器中进行运动估计是使用该方式。

卡尔曼滤波器

滤波器根据上一个时刻的值来估计当前时刻的状态，得到k时刻的先验估计值，然后使用当前时刻的测量值来更正这个估计值得到当前状态的估计值。=
我们将卡尔曼滤波看做一种运动模型==，用来对目标的位置进行预测，并且利用预测结果对跟踪的目标进行修正，属于自动控制理论中的一种方法。
如果目标运动速度比较快，或者进行隔帧检测时，在后续帧中，目标A已运动到前一帧B所在位置，这时再进行关联就会得到错误的结果。
如何避免出现这种关联错误，可以在进行目标关联之前，对目标在后续帧中出现的位置进行预测，然后与预测结果进行对比关联。
我们在对比关联之前，先预测出A和B在下一帧中的位置，然后再使用实际检测位置与预测的位置进行对比关联，只要预测足够精确，几乎不会出现由于速度太快而存在的误差。
卡尔曼滤波就可以用来预测目标在后续帧中出现的位置。
卡尔曼滤波器最大的优点是采用递归的方法来解决线性滤波问题，它只需要当前的测量值和前一个周期的预测值就能进行状态估计。这种递归方法不需要大量的存储空间，每一步的计算量小，计算步骤清晰，非常适合计算机处理。
原理介绍：
无论计算还是检测都会存在一定的误差，所以我们只能认为当前状态是器真实状态的一个最优估计。设当前状态服从一个高斯分布。高斯分布的中心。因为有两个变量，所以可以用一个协方差矩阵来表示数据之间的相关性和离散程度。
下一个时刻的状态，Fk为状态转移矩阵。

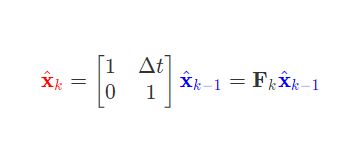
系统的不确定性和相关性可以通过协方差矩阵描述，那么根据当前协方差矩阵预测下一时刻的协方差矩阵。

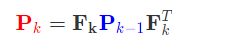
增加小车的内部控制

B状态控制矩阵，u为状态控制向量，前者表示加速减速如何改变小车的状态，后者表示控制的力度和大小。
考虑系统的外部影响

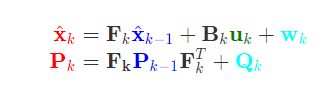
当前状态和观测状态之间的关系：通过预测值得到观测值的预测。

卡尔曼滤波需要做的最重要的核心的事情就是融合预测和观测的结果，充分利用两者的不确定性来得到更加准确的估计。

通过预测和观测值的高斯分布的乘积得到的即是卡尔曼滤波的最优估计。

实际中的卡尔曼滤波：
预测阶段：

更新阶段：

卡尔曼滤波器实践

初始化：预先设定状态变量dim_x和观测变量维度dim_z,协方差矩阵P、运动形式和观测矩阵H等，一般各个协方差矩阵都会初始化为单位矩阵，根据特定的场景需要相应的设置。
预测阶段：为了保证通用性引入以往系数，其作用在于调节过往信息的依赖程度，遗忘系数越大对历史信息的依赖越小。
更新阶段：
小车案例：

import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
from filterpy.kalman import KalmanFilter

#小车运动数据生成假设速度为1的匀速运动
#生成1000个位置，是小车的实际位置
z=np.linspace(1,1000,1000)
#添加噪声
mu,sigma=0,1
noise=np.random.normal(mu,sigma,1000)
#小车的观测值
z_noise=z+noise

#参数初始化
my_filter=KalmanFilter(dim_x=2,dim_z=1)#状态向量以及测量值
#定义卡尔曼滤波中所需的参数
my_filter.x=np.array([[0.],[0.]])
#这个初始值不重要，在利用观测值进行更新迭代后会接近真实值

#协方差矩阵,假设速度和位置没关系
my_filter.P=np.array([[1.,0.],[1,0.]])
#状态转移矩阵
my_filter.F=np.array([[1.,1.],[0.,1.]])

#状态转移协方差矩阵也就是外界噪声
my_filter.Q=np.array([[0.0001,0.],[0.,0.0001]])

#观测矩阵
my_filter.H=np.array([[1,0]])
#测量噪声，方差为1
my_filter.R=1

#卡尔曼滤波进行预测
z_new_list=[]
v_new_list=[]
for k in range(len(z_noise)):
    #预测过程
    my_filter.predict()
    #利用观测值进行更新
    my_filter.update(z_noise[k])
    x=my_filter.x
    #收集卡尔曼滤波后的速度和位置信息
    z_new_list.append(x[0][0])
    v_new_list.append(x[1][0])

# 位移的偏差
dif_list = []
for k in range(len(z)):
    dif_list.append(z_new_list[k]-z[k])
# 速度的偏差
v_dif_list = []
for k in range(len(z)):
    v_dif_list.append(v_new_list[k]-1)
plt.figure(figsize=(20,9))
plt.subplot(1,2,1)
plt.xlim(-50,1050)
plt.ylim(-3.0,3.0)
plt.scatter(range(len(z)),dif_list,color ='b',label = "位置偏差")
plt.scatter(range(len(z)),v_dif_list,color ='y',label = "速度偏差")
plt.legend()
plt.show()

主要初始化参数：初始的状态变量，F,P状态转移矩阵，协方差矩阵，噪声和观测值的协方差矩阵。