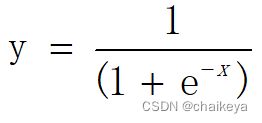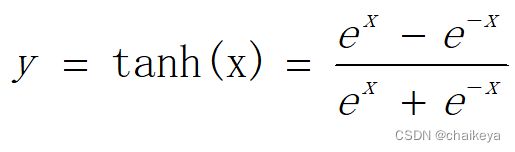卷积神经网络中的激活函数sigmoid、tanh、relu
目录
1、什么是激活函数?
2、为什么要在卷积层后面添加激活函数?
3、激活函数的性质
3.1 sigmoid 激活函数
3.2 tanh 激活函数
3.3 ReLU 激活函数
4、如何选择激活函数?
5、神经网络中的隐藏层是什么?
神经网络中的一个个神经元实质上是一个线性变换和非线性的激活函数的操作。
1、什么是激活函数?
一个神经元会同时接收多个信号,然后将这些信号乘以一定权重求和,再用函数处理后再输出新的信号。对神经元的输入进行处理,以获得输出的函数称为激活函数。
2、为什么要在卷积层后面添加激活函数?
如果只有线性变换,那无论多少层神经元,都能简化层一层神经元,那神经网络只是简单多元线性回归而已,不能拟合更加复杂的函数。举个例子,如果我们只有线性操作,那么我们的神经网络永远无法拟合圆等复杂的曲线图形,永远只能表示超平面,无法表示曲面等。
激活函数的目的:将神经网络非线性化,即提升神经网络的拟合能力,能拟合更复杂的函数。
- 激活函数对模型学习、理解非常复杂和非线性的函数具有重要作用。
- 激活函数可以引入非线性因素。如果不使用激活函数,则输出信号仅是一个简单的线性函数。线性函数一个一级多项式,线性方程的复杂度有限,从数据中学习复杂函数映射的能力很小。没有激活函数,神经网络将无法学习和模拟其他复杂类型的数据,例如图像视频、音频、语音等。
- 激活函数可以把当前特征空间通过一定的线性映射转换到另一个空间,让数据能够更好的被分类。
3、激活函数的性质
- 连续的:当输入值发生较小的改变时,输出值也发生较小的改变;
- 可导的:在定义域中,每一处都是存在导数;
从定义来看,几乎所有的连续可导函数都可以用作激活函数。但目前常见的多是分段线性和具有指数形状的非线性函数。
在实际的应用中,我们需要先了解以下概念:
饱和
当一个激活函数 h(x) 满足 limn→+∞h′(x)=0 时,我们称之为右饱和。
当一个激活函数 h(x) 满足 limn→−∞h′(x)=0 时,我们称之为左饱和。
当一个激活函数,既满足左饱和又满足又饱和时,我们称之为饱和。
硬饱和与软饱和
对任意的x,如果存在常数c,当 x > c 时恒有 h′(x)=0 则称其为右硬饱和。
对任意的x,如果存在常数c,当 x < c 时恒有 h′(x)=0 则称其为左硬饱和。
若既满足左硬饱和,又满足右硬饱和,则称这种激活函数为硬饱和。
如果只有在极限状态下偏导数等于0的函数,称之为软饱和。
3.1 sigmoid 激活函数
sigmoid是平滑的阶梯函数,可导。sigmoid可以将任何值转换成0~1概率,用于二分类。
公式:
导数:
导数2:
sigmoid 在定义域内处处可导,根据上述对饱和的定义,其可被定义为软饱和激活函数。
Sigmoid 的软饱和性,使得深度神经网络在二三十年里一直难以有效的训练,是阻碍神经网络发展的重要原因。具体来说,由于在后向传递过程中,sigmoid向下传导的梯度包含了一个f’(x) 因子(sigmoid关于输入的导数),因此一旦输入落入饱和区,f’(x) 就会变得接近于0,导致了向底层传递的梯度也变得非常小。此时,网络参数很难得到有效训练。这种现象被称为梯度消失。一般来说,sigmoid 网络在 5 层之内就会产生梯度消失现象。
这里给出一个关于梯度消失的通俗解释:
Sigmoid 函数能将负无穷到正无穷的数映射到0和1之间,并且对这个函数求导的结果是 f′(x)=f(x)(1−f(x))。因此两个0到1之间的数相乘,得到的结果就会变得很小了。神经网络的反向传播是逐层对函数偏导相乘,因此当神经网络层数非常深的时候,最后一层产生的偏差就因为乘了很多的小于1的数而越来越小,最终就会变为0,从而导致层数比较浅的权重没有更新。
由于sigmoid的导数值小于1/4,x变化的速率要快于y变化的速率,随着层数的增加,连续不断执行sigmoid函数,就会导致,前面更新较大的幅度,后面更新较小的幅度,因此,网络在学习过程中,更倾向于更新后面(靠近输出层)的参数,而不是前面的参数(靠近输入层)。
Sigmoid 函数的优缺点:
优点:
- Sigmoid 函数的输出映射在(0,1)之间,单调连续,输出范围有限,优化稳定,可以用作输出层。它在物理意义上最为接近生物神经元。
- 求导容易。
缺点:
- 其输出并不是以0为中心的。
- 激活函数的计算量较大,在反向传播中,当求误差梯度时,求导涉及除法;
- 函数的敏感区间较短,(-1,1)之间较为敏感,超过区间,则处于饱和状态。
- 由于其软饱和性,在反向传播中,容易就会出现梯度消失,导致训练出现问题,无法完成深层网络的训练;
3.2 tanh 激活函数
公式:
导数:
同样的,Tanh 激活函数也具有软饱和性。Tanh 网络的收敛速度要比 Sigmoid 快。因为 Tanh 的输出均值比 Sigmoid 更接近 0,SGD 会更接近 natural gradient(一种二次优化技术),从而降低所需的迭代次数。
Tanh 激活函数的优缺点:
优点:
- 比Sigmoid函数收敛速度更快。
- 相比Sigmoid函数,其输出以0为中心。
缺点:
还是没有改变Sigmoid函数的最大问题——由于饱和性产生的梯度消失。
3.3 ReLU 激活函数
公式:
可见,ReLU 在x<0 时硬饱和。由于 x>0时导数为 1,所以,ReLU 能够在x>0时保持梯度不衰减,从而缓解梯度消失问题。但随着训练的推进,部分输入会落入硬饱和区,导致对应权重无法更新。这种现象被称为“神经元死亡”。
ReLU 函数的优缺点:
优点:
- 相比起Sigmoid和tanh,ReLU在SGD中能够快速收敛。据称,这是因为它线性、非饱和的形式。
- Sigmoid和tanh涉及了很多很expensive的操作(比如指数),ReLU可以更加简单的实现。
- 有效缓解了梯度消失的问题。
- 在没有无监督预训练的时候也能有较好的表现。
- 提供了神经网络的稀疏表达能力。
缺点:
随着训练的进行,可能会出现神经元死亡,权重无法更新的情况。如果发生这种情况,那么流经神经元的梯度从这一点开始将永远是0。也就是说,ReLU神经元在训练中不可逆地死亡了。
4、如何选择激活函数?
- 在输出层,一般会使用sigmoid函数,因为一般期望的输出结果概率在0~1之间。如二分类(输出是0、1),sigmoid可作为输出层的激活函数,然后其它的所有单元都选择Relu函数。
- 在隐藏层,tanh函数优于sigmoid函数。因为其取值范围介于-1 ~ 1之间,有类似数据中心化的效果。
- 如果在隐藏层上不确定使用哪个激活函数,那么通常会使用Relu激活函数。有时,也会使用 tanh激活函数,Relu的一个优点是:当是负值的时候,导数等于0。
- 在实际应用中,tanh和sigmoid会在端值趋于饱和,造成训练速度减慢,故一般的深层网络的激活函数默认大多采用relu函数,也可以前面几层使用relu函数,后面几层使用sigmoid函数。
- sigmoid 激活函数:除了输出层是一个二分类问题基本不会用它。
- tanh 激活函数:tanh是非常优秀的,几乎适合所有场合。
- ReLu激活函数:最常用的默认函数,如果不确定用哪个激活函数,就使用ReLu或者Leaky ReLu,再去尝试其他的激活函数。
- 如果遇到了一些死的神经元,我们可以使用Leaky ReLU函数。
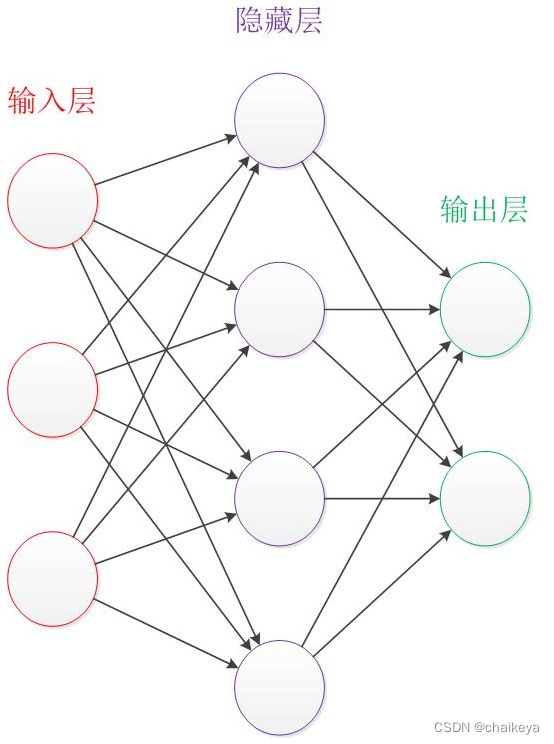
5、神经网络中的隐藏层是什么?
通常,卷积神经网络除了输入和输出层之外还有四个基本的神经元层,在三层神经网络中,这基层被称为隐藏层
卷积层(Convolution)
激活层(Activation)
池化层(Pooling)
完全连接层(Fully connected)
参考资料:
激活函数sigmoid、tanh、relu - 百度文库
机器学习——sigmoid、tanh、relu等激活函数总结 - 百度文库
深度学习入门与Pytorch|3.4 神经网络中加入非线性变换 - 知乎
https://www.csdn.net/tags/OtDaggysMDI4NzItYmxvZwO0O0OO0O0O.html
常用的激活函数对比_打工人小飞的博客-CSDN博客_激活函数对比