《机器学习》笔记:第二章模型评估与选择(Python代码实现)
2.1 经验误差与过拟合
(一)经验误差
| 基本术语 | 释义 |
|---|---|
| 错误率 | 分类错误的样本数占总样本数的比例 |
| 精度 | 精度=1-错误率 |
| 训练误差 | 在训练集上的误差 |
| 泛化误差 | 在新样本上的误差 |
(二)过拟合
- 过拟合:模型训练样本训练的太好,甚至将训练样本自身的一些特点当作了所有潜在样本都会具有的一般性质,这样就会导致泛化性能下降。
- 欠拟合:对训练样本的一般性质尚未学好
一般来说,欠拟合比较好解决,而过拟合无法彻底避免,只能尽量“缓解”(若可彻底避免过拟合,则说明可以获得最优解,即通过构造证明了“P=NP”)。
2.2 评估方法
为了衡量一个模型的泛化能力,需要使用“测试集”来测试模型对新样本的判别能力,以测试集上的“测试误差”作为泛化误差的近似。
测试集应遵循与训练集互斥的原则。
(一)留出法
-
直接将数据集 D D D分为两个互斥集合,需要兼顾模型样本均衡性,必要时可采用分层抽样的方法。
-
单次使用留出法结果不够可靠,需要若干次随机划分,重复进行实验评估后取平均。
-
通常选择2/3~4/5的样本作为训练集,剩余作为测试集。
#加载库
import numpy as np
import pandas as pd
#创建数据集
data=np.random.randint(100,size=[25,4])
#创建分割函数(此段代码为shenhuaifeng发布)
def split_train(data,test_ratio):
shuffled_indices=np.random.permutation(len(data))
test_set_size=int(len(data)*test_ratio)
test_indices =shuffled_indices[:test_set_size]
train_indices=shuffled_indices[test_set_size:]
return data[train_indices],data[test_indices]
#切分训练集
train_data,test_data=split_train(data,0.2)
(二)交叉验证法
- 子集划分:交叉验证法先将数据集 D D D划分为 k k k个大小相似的互斥子集,每个子集 D i D_i Di都通过分层抽样获得。
- 训练集挑选:每次用“ k − 1 k-1 k−1”个子集的并作为训练集,余下1个作为测试集。如是反复, k k k次后取平均。
- k k k值一般取10。
#加载库
from sklearn import datasets
from sklearn import metrics
from sklearn.model_selection import KFold,cross_val_score
from sklearn.pipeline import make_pipeline
from sklearn.linear_model import LogisticRegression
from sklearn.preprocessing import StandardScaler
# 加载手写数字的数据集
digits = datasets.load_digits()
# 创建特征矩阵
features = digits.data
#创建目标向量
target = digits.target
#创建标准化对象
standardizer =StandardScaler()
# 创建逻辑回归对象
logit=LogisticRegression()
#创建包含数据标准化和逻辑回归的流水线
pipeline = make_pipeline(standardizer,logit)
#创建k折交叉验证对象
kf = KFold(n_splits=10,shuffle=True,random_state=1)
#创建k折交叉验证
cv_results = cross_val_score(pipeline,features,target,cv=kf,scoring="accuracy")
# 计算得分
cv_results
#计算平均得分
cv_results.mean()
(三)自助法
自助法能够避免因划分区间而产生的训练集样本规模减小问题。
- 以bootstrap sampling为基础。给定包含 m m m个样本的数据集 D D D,对其进行 m m m次采样,每次随机挑选1个样本,组成采样数据集 D ′ D' D′。
- 样本在 m m m次采样中始终不被采到的概率为 ( 1 − 1 m ) m (1-\frac{1}{m})^m (1−m1)m,取极限约等于 1 e ≈ 0.368 \frac{1}{e} \approx 0.368 e1≈0.368。
- 利用 D ′ D' D′作为训练集, D / D ′ D/D' D/D′作为测试集,该种测试结果称为“包外估计”。
- 一般在数据量不足时采用
#载入包
import numpy as np
#创建数据集
data=np.random.randint(100,size=[25,4])
#定义自助法函数
def bootstrap_train(data):
bootstrapping = []
#自主法抽取样本号
for i in range(len(data)):
bootstrapping.append(np.floor(np.random.random()*len(data)))
train_set = []
#按样本号抽取样本保存为train_set
for i in range(len(data)):
train_set.append(data[int(bootstrapping[i])])
#将train_set存储为np数组
train_set = np.array(train_set)
data_rows = data.view([('', data.dtype)] * data.shape[1])
train_rows = train_set.view([('', train_set.dtype)] * train_set.shape[1])
#data与train_data求差集
test_data = (np.setdiff1d(data_rows, train_rows).view(data.dtype).reshape(-1, data.shape[1]))
return train_set,test_data
train_data,test_data=bootstrap_train(data)
2.3 性能度量
回归任务中最常用的性能度量“均方误差”(MSE)。
E ( f ; D ) = 1 m ∑ i = 1 m ( f ( x i ) − y i ) 2 E(f;D)=\frac{1}{m}\sum^m_{i=1}(f(x_i)-y_i)^2 E(f;D)=m1i=1∑m(f(xi)−yi)2
(一)错误率与精度
对于样本集 D D D,分类错误率定义为:
E ( f ; D ) = 1 m ∑ i = 1 m Π ( f ( x i ) ≠ y i ) E(f;D)=\frac{1}{m}\sum^m_{i=1}\Pi(f(x_i)\neq y_i) E(f;D)=m1i=1∑mΠ(f(xi)=yi)
精度则定义为:
a c c ( f ; D ) = ∑ i = 1 m Π ( f ( x i ) ) y i ) = 1 − E ( f ; D ) acc(f;D)=\sum^m_{i=1}\Pi(f(x_i)) y_i)=1-E(f;D) acc(f;D)=i=1∑mΠ(f(xi))yi)=1−E(f;D)
#加载包
import numpy as np
from sklearn.metrics import accuracy_score
#准备数据
real = [0,0,1,0,1,0]
pred = [1,0,1,1,1,0]
#错误率
error_rate=1-accuracy_score(real,pred)
#精度
acc=accuracy_score(real,pred)
(二)查准率、查全率与F1
| 基本术语 | 英文 |
|---|---|
| 查准率 | precision |
| 查全率 | recall |
| 真正例 | true positive (TP) |
| 假正例 | false positive (FP) |
| 真反例 | true negative (TN) |
| 假反例 | false negative (FN) |
查准率(准确率):
p r e c i s i o n = T P T P + F P precision = \frac{TP}{TP+FP} precision=TP+FPTP
查全率(召回率):
r e c a l l = T P T P + F N recall = \frac{TP}{TP+FN} recall=TP+FNTP
- 查准与查全一般情况下两者不可兼得。
F 1 F1 F1:
F 1 = 2 × p r e c i s i o n × r e c a l l p r e c i s i o n + r e c a l l F1=\frac{2 \times precision \times recall}{precision+recall} F1=precision+recall2×precision×recall
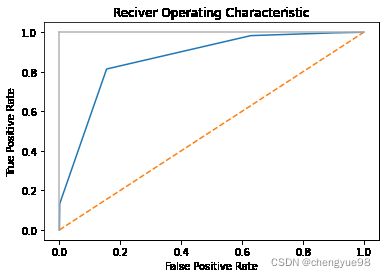
(三)ROC与AUC
ROC纵轴为真正例率(TPR),横轴为假正例率(FPR)。
T P R = T P T P + F N TPR = \frac{TP}{TP+FN} TPR=TP+FNTP
F P R = F P T N + F P FPR =\frac{FP}{TN+FP} FPR=TN+FPFP
AUC为ROC曲线下各部分面积之和。
#载入包
import numpy as np
import matplotlib.pyplot as plt
#读入TPR与FPR数据
true_positive_rate = np.array([0,0.133,0.814,0.983,0.997,1])
false_positive_rate = np.array([0,0.001,0.155,0.629,0.904,1])
#绘图
plt.title("Reciver Operating Characteristic")
plt.plot(false_positive_rate,true_positive_rate)
plt.plot([0,1],ls="--")
plt.plot([0,0],[1,0],c=".7"),plt.plot([1,1],c=".7")
plt.xlabel("False Positive Rate")
plt.ylabel("True Positive Rate")
plt.show()