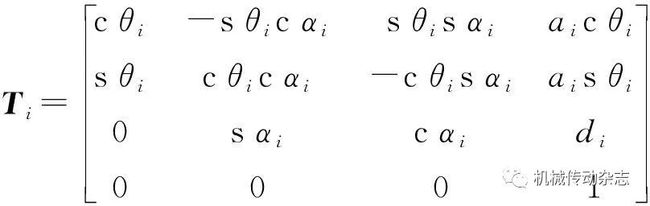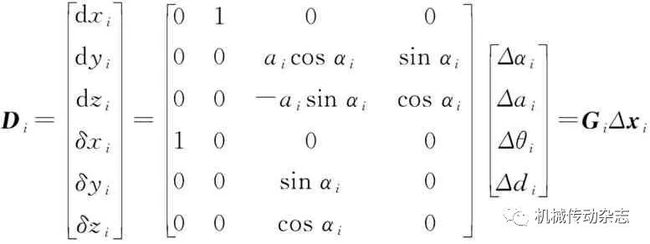椭球拟合的电子罗盘磁差补偿_【推荐文章】三臂凿岩台车钎杆的绝对定位误差补偿研究...

《机械传动》2018年  第42卷   第10期

文章编号：1004-2539(2018)10-0001-05

DOI:10.16578/j.issn.1004.2539.2018.10.001

引用格式：夏毅敏, 李正光, 罗建利,等. 三臂凿岩台车钎杆的绝对定位误差补偿研究[J]. 机械传动, 2018, 42(10):1-5.

XIA Yimin，LI Zhengguang，LUO Jianli，et al.Study on absolute positioning error compensation for the drill rod of the three-arm rock-drilling jumbo[J].Journal of Mechanical Transmission, 2018, 42(10):1-5.

三臂凿岩台车钎杆的绝对定位误差补偿研究

夏毅敏^1，2   李正光^1，2   罗建利³  马劼嵩^1，2 (1 中南大学 机电工程学院，湖南 长沙 410083) (2 中南大学 高性能复杂制造国家重点实验室，湖南 长沙 410083) (3 中国铁建重工集团有限公司，湖南 长沙 410083) 摘要 为提高三臂凿岩台车钎杆的绝对定位精度，首先，基于有限元仿真，采用正交试验法确定影响臂架柔性误差的主要参数，得到柔性误差补偿公式；之后，对受力关节坐标系进行变换，建立基于位置误差的运动学误差标定模型，并对模型中待标定参数进行冗余性分析，剔除冗余参数；最后，以激光全站仪为测量设备，利用LM算法对待标定参数进行求解，验证运动学标定效果。结果表明，该方法有效地补偿了钎杆绝对定位误差，钎杆的绝对定位误差降低了79.6%。 关键词 三臂凿岩台车 运动学标定 正交试验 柔性补偿

0 引言

三臂凿岩台车是一种集机械、电子、液压等多学科技术于一体的隧道施工设备。与传统凿岩设备相比，三臂凿岩台车能有效控制超挖量，提高钻爆效率，降低因地质原因引起的施工事故，保障工作人员的施工安全[1-3]。施工过程中，第一个关键技术为钎杆的快速准确定位，但是钎杆的绝对定位精度经常出现不满足工程实际需求的情况，严重影响了隧道施工效率和施工质量。三臂凿岩台车钎杆的绝对定位误差补偿对隧道施工有重要意义。

三臂凿岩台车的标定涉及臂架柔性误差补偿和运动学误差标定两个方面。目前，工业机器人常用误差补偿方法分为运动学标定和非运动学标定。运动学标定是针对各关节坐标系的DH参数进行补偿[4-5]，非运动学标定主要是对连杆的柔性变形进行误差补偿。近年来，国内外学者通过标定对机器人的定位误差补偿进行了大量研究，对于小型负载机器人，没有考虑连杆的柔性变形，即非运动学标定，只补偿DH参数误差和关节柔性误差，标定后绝对定位误差精度满足实际工业需求[6-8]。但是，对于大型工业负载机器人，连杆的柔性误差补偿对绝对定位精度影响更大[9-11]。

为此，作者以DH法建立臂架正向运动学模型，综合考虑运动学标定和非运动学标定中的臂架柔性变形，建立了位置误差标定模型，通过参数辨识获得DH模型参数保证三臂凿岩台车钎杆的绝对定位精度。

1 臂架正向运动学建模

1.1 臂架结构介绍

凿岩台车臂架包括6个回转关节和2个移动关节，钎杆安装在推进梁上。其主要结构如图1所示。

1.2 臂架运动学建模

限于篇幅，本文中仅对锚杆油缸固定的一般工况进行讨论，即锚杆关节θ7为过渡关节，θ7=0。根据臂架结构进行DH建模，最终臂架运动学模型如图2所示，臂架D-H参数如表1所示。

图1 凿岩台车臂架结构图

图2 臂架正向运动学模型

表1 臂架D-H参数表

将参数代入关节坐标变换矩阵，即式(1)，得到臂架正向运动学模型如式(2)所示。

(1)

式中，i表示第i个关节，

(2)

2 绝对定位误差标定模型建立

影响三臂凿岩台车臂架运动学模型位姿误差的主要因素分为柔性误差和运动学误差。柔性误差包括外力、惯性力等导致的臂架弹性变形和振动误差。运动学误差主要包括臂架结构DH参数误差。本文中臂架柔性误差主要针对大臂伸缩臂末端挠度变形和端截面转角变形进行补偿，关节的柔性变形误差则通过运动学标定，于运动学误差中补偿。

2.1 臂架柔性误差补偿

2.1.1 臂架挠度和转角变形影响参数分析

大臂伸缩运动是由大臂内臂基于外臂滑块的相对运动实现的。由于大臂末端到推进梁部件总质量超过2 t，大臂外臂滑块会产生较大变形，极限工况下其应力最高可达520 MPa，最大应力位置如图3所示。滑块末端变形会影响大臂末端挠度和端截面转角补偿效果，故在柔性误差补偿时需考虑滑块变形和间隙的影响。

影响臂架挠度和端截面转角的参数为大臂伸缩d3、大臂俯仰θ2、推进梁伸缩θ4和推进梁俯仰d8。影响参数较多，难以全部考虑，因此首先确定柔性误差的主要参数。基于有限元静力学仿真，不考虑影响因素间的交互作用，采用正交试验法对影响柔性误差的关节参数进行4因素3水平L9(34)分析。正交试验安排与结果如表2所示。根据极差值可以看出，大臂伸缩d3和大臂俯仰θ2影响最大，为主要因素；推进梁伸缩d8和推进梁俯仰θ4为非主要因素。

图3 大臂外臂静力学变形

表2 正交试验安排与结果

2.1.2 臂架挠度和转角变形计算

对大臂伸缩d3和大臂俯仰θ2可运动范围进行区间划分，考虑到大臂伸缩关节达到极限位置时滑块应力集中的影响，将运动区间划分为：d3=[0.25，0.75，1.25，1.75，2.25，2.5]；θ2=[30，12，-6，-24，-42，-60]。驱动臂架至36组对应关节值，其余非主要影响关节值取0，测试大臂伸缩关节末端对应的挠度变形和转角变形，并对所得变形值进行非线性拟合，当前臂架的柔性误差公式如式(3)、式(4)所示。所得拟合公式与测试数据对比如图4、图5所示。其中，挠度变形和转角变形的相关系数分别为0.98和0.96。

Δw=-0.08-0.18d3+0.66d32+0.14cos θ2-

0.01(cos θ2)2+0.06d3(cos θ2)2

(3)

Δθ=-0.56-0.16d3+0.06d32+0.8cos θ2+

0.49d3cos θ2

(4)

图4 柔性变形挠度补偿

图5 柔性变形端截面转角补偿

2.1.3 臂架柔性误差补偿

对大臂末端进行柔性误差补偿，将挠度变形Δw和端截面转角变形Δθ代入传递矩变换方式如图6所示。

图6 动态误差补偿坐标变换

图6中，坐标系O4先沿y4轴移动挠度值Δw，再沿z4轴旋转端截面转角Δθ，变换至坐标系再进行坐标系传递变换至变换关系为

T3·Trans(0，Δw，0)·Rot(z，Δθ)·T4=

(5)

此时，臂架正向运动学模型为

(6)

2.2 臂架位置误差运动学标定模型

2.2.1 臂架位置误差运动学标定模型建立

在建立臂架正向运动学模型并对柔性变形进行补偿后，可以采用工业机器人标定方法对臂架静态误差标定，降低钎杆的绝对定位误差。

对各关节传递矩阵结构参数求偏导，结果如式(7)所示。

(7)

结合臂架微分运动公式，可获得当前关节i的微分运动误差为

(8)

式中，Gi为臂架连杆的结构参数误差系数矩阵；Δxi为结构参数。

在建立臂架标定模型时，除了考虑臂架各关节的结构参数(α，a，θ，d)误差，还需考虑测量坐标系到基坐标系微分运动。在标定时，测量坐标系与基坐标系轴线重合。设从测量坐标系到臂架基坐标系的微分平移参数和转动参数分别为dx0、dy0、dz0和δx0、δy0、δz0，则测量坐标系到基坐标系的微分误差为

(9)

将臂架所有坐标系的微分误差变换到钎杆坐标系，得到钎杆末端定位误差D为

(10)

式中，为当前坐标系i与钎杆坐标系n的雅可比转换矩阵，

分别对定位误差和误差传递矩阵取前3行，即

(11)

(12)

式中，H为维度3×(4n+6)的误差传递矩阵。

则臂架的位置误差标定模型为

dP=H·Δx

(13)

式中，Δx为维度(4n+6)×1的结构误差参数。

2.2.2 标定模型冗余参数分析

由于三臂凿岩台车为6R2P型工业机器人，结合测量坐标系微分误差，共有38个待标定参数。但是这些参数并非线性无关的，参数之间存在耦合。待标定参数的冗余问题会导致标定效果变差，甚至出现无法标定情况。因此需要将待标定参数中的冗余参数剔除。

待标定参数分为独立参数、相关参数和无关参数。其中，相关参数和无关参数均属于冗余参数。对于位置误差标定模型，至少需要测量13个钎杆末端位置才能确定完整的待标定参数。构建完整的误差传递矩阵，并对其进行最简形变换，分析传递矩阵的列相关性，结果如表3所示。冗余参数共有11个，剔除冗余参数，并将误差传递矩阵对应的列剔除，最终待标定参数为27个。

表3 待标定参数冗余性分析

2.3 臂架标定算法

为提高标定效果，选取臂架移动全范围中的30个点坐标作为误差模型输入值，此时方程个数为90，远大于待标定参数，故采用LM算法(Levenberg-Marquardt算法)对待标定参数进行拟合，求解目标函数Δx的具体步骤如下：

(1)计算定位误差dP。将测试所得钎杆末端30个点坐标记为P90×1，把对应关节值代入动态误差补偿后的正运动学模型，得到此时钎杆末端名义位置计算

(2)将目标函数Δx赋初始值为设定LM算法初始阻尼系数λ=0.001，算法迭代次数为200。把对应参数代入H90×27，得到此标定模型下的误差传递矩阵。

(3)计算定位误差ek。根据当前Δxk值，计算dPk=H*Δxk，并计算当前定位误差ek=(dP-dPk)T·(dP-dPk)。

(4)计算定位误差计算ek+1。此时待标定参数Δxk+1=Δxk-(HTH+λI)-1HTdPk，计算得到新的定位误差dPk+1，并计算定位误差ek+1。

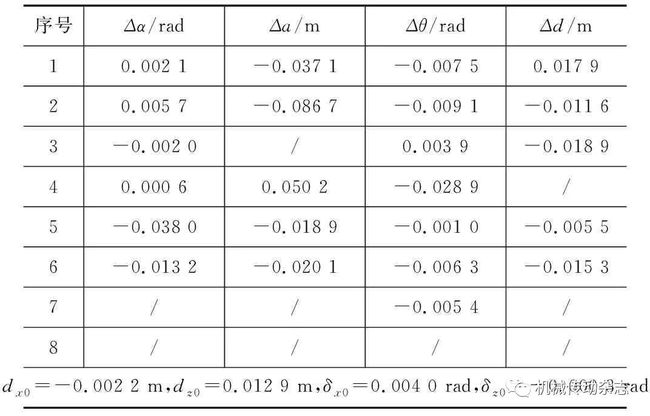
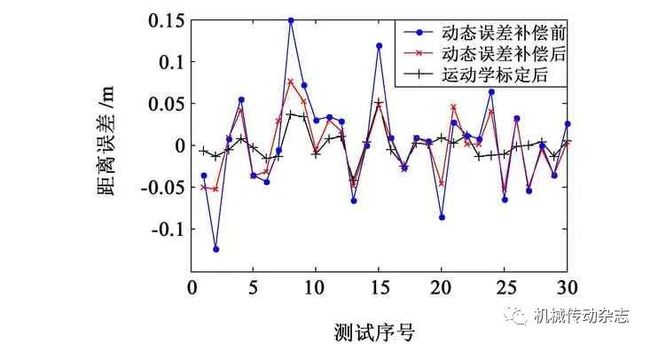
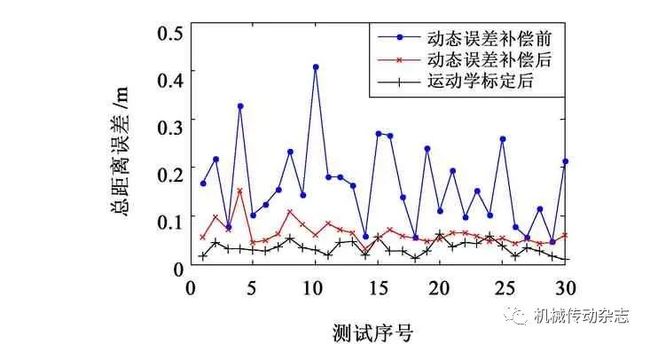
(5)判断ek+1

(6)判断迭代达到指定次数，输出待标定参数值。

3 标定实验研究

本文实验使用Leica激光全站仪作为测量设备对三臂凿岩台车的右臂进行标定，标定方式如图7所示。在臂架工作空间中采集30个点的坐标，待标定参数计算结果如表4所示。

图7 测试现场

表4 标定结果

对比标定前和标定后的三向坐标误差以及距离误差，结果如图8～图11所示。在运动学标定后，X方向绝对定位误差降低20.5%，Y方向降低85.1%，Z方向降低73.7%，总距离误差降低79.6%。其中，运动学模型在柔性误差补偿前的绝对定位误差最大值为0.411 m，最小值为0.048 m，平均值为0.165 m，均方差为0.087 0；在柔性误差补偿后的绝对定位误差最大值为0.153 m，最小值为0.031 m，平均值为0.063 m，均方差为0.024；在运动学标定后的绝对定位误差最大值为0.063 m，最小值为0.010 m，平均值为0.034 m，均方差为0.014。在施工过程中，三臂凿岩台车钎杆的实际定位要求小于0.1 m，标定后的运动学模型满足要求。

图8 标定前后X方向绝对定位误差

图9 标定前后Y方向绝对定位误差

图10 标定前后Z方向绝对定位误差

图11 标定前后总距离绝对定位误差

4 结论

针对三臂凿岩台车的钎杆绝对定位误差补偿问题，综合考虑臂架柔性变形误差和运动学标定方法，建立运动学误差标定模型。对运动学参数进行辨识时，针对三臂凿岩台车6R2P冗余自由度结构，对冗余参数进行判别和剔除，采用LM算法对待标定参数进行拟合以提高标定效果。实验结果表明，标定后的钎杆绝对定位误差降低了79.6%，利用该运动学误差标定模型对三臂凿岩台车进行绝对定位误差补偿有较好的试验效果。

参考文献

[1] KIM Y，MOON H. Application of the guideline for overbreak control in granitic rock masses in Korean tunnels[J]. Tunneling and Underground Space Technology，2013，35:67-77.

[2] WANG H S，ZHAN D Y，HUANG P L，et al. Inverse kinematics of a heavy duty manipulator with 6-DOF based on dual quaternion[J]. Journal of Central South University，2015，22(7):2568-2577.

[3] JIANG Q，AHMED S N. The kinematics of 6R-2P mining drill jumbo[J]. Journal of Mechanisms and Robotics，2014，6(3):034501.

[4] 杨小磊，丛明，刘冬，等. 六自由度工业机器人运动学标定方法[J]. 华中科技大学学报(自然科学版)，2015(S1):41-44.

[5] 杨源，曹彤，刘达. 一种利用标定板的机械臂DH参数标定方法[J]. 机械传动，2017，41(6):178-181.

[6] NOBIOLA A，BONEV I A. Absolute calibration of an ABB IRB 1600 robot using a laser tracker[J]. Robotics and Computer-Integrated Manufacturing，2013，29(1):236-245.

[7] 王旭，李东升，王明明. 工业机器人大负载刚度辨识及误差补偿研究[J]. 机械传动，2017，41(5):30-33.

[8] DUMAS C，CARO S，CHERIF M. Joint stiffness identification of industrial serial robots[J]. Robotica，2012，30(4):649-659.

[9] 刘志，赵正大，谢颖，等. 考虑结构变形的机器人运动学标定及补偿[J]. 机器人，2015(3):376-384.

[10] NGUYEN H，ZHOU J，KANG H. A calibration method for enhancing robot accuracy through integration of an extended Kalman filter algorithm and an artificial neural network[J]. Neurocomputing，2015，151(3):996-1005.

[11] 陈钢，王蕾，贾庆轩，等. 基于MCPC模型的机器宇航员运动学参数标定方法与实验[J]. 机器人，2017，39(2):151-159.

Study on Absolute Positioning Error Compensation for the Drill Rod of the Three-arm Rock-drilling Jumbo

Xia Yimin1,2 Li Zhengguang1,2 Luo Jianli3 Ma Jiesong1,2

(1 School of Mechanical and Electrical Engineering, Central South University, Changsha 410083, China)

(2 State Key Laboratory of High Performance Complex Manufacturing, Central South University, Changsha 410083, China)

(3 China Railway Construction Heavy Industry Co., Ltd., Changsha 410083, China)

Abstract In order to improve the absolute positioning accuracy for the drill rod of the three-arm rock-drilling jumbo，firstly，based on the finite element simulation, the main parameters that affect the flexible error of the arm are determined by the orthogonal test method，and the flexible error compensation formula is obtained. Then，after the transformation of the force joint coordinate system，the calibration model is set up based on the kinematics position error，and the redundant parameters are eliminated in the model by redundancy analysis. Finally，the laser total station is used as the measuring device, and the LM algorithm is used to solve the calibration parameters to verify the kinematics calibration effect. The results show that the method effectively compensates the absolute positioning error of the drill rod, the absolute positioning error of the drill rod is reduced by 79.6%.

Key words Three-arm rock-drilling jumbo Kinematics calibration Orthogonal test Flexible compensation

收稿日期：2018-01-06

基金项目：国家高技术研究发展计划(863计划)(2012AA041803)中央高校基本科研业务费专项资金资助(2017zzts400)

作者简介：夏毅敏(1967— )，男，江西永新人，博士，教授，研究方向为大型遂道掘进装备。

专家点评：  

    论文为提高三臂凿岩台车钎杆的绝对定位精度，采用正交试验法确定影响臂架柔性误差的主要参数，建立了基于位置误差的运动学误差标定模型，最后以激光全站仪为测量设备，利用LM算法对待标定参数进行求解，并验证运动学标定效果。研究工作具有较大的工程应用价值。

END

查看更多内容，请点击