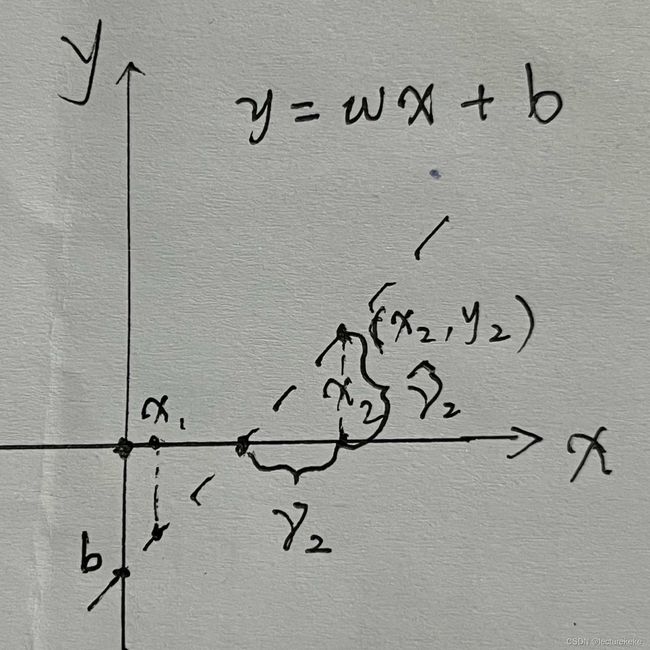理解函数间隔与几何间隔

从一维输入的支持向量机说起

如上图，一维输入的函数图像需要在二维坐标中表现。根据定义很容易得出：分离超平面是唯一的，这里分离超平面是一个点，函数\(y=\omega x+b\)与x轴相交于这个点。经过分离点的直线有无数条，因此\(\omega\)和b有无数取值。图中几何间隔\(\gamma_2\)不会变，函数间隔\(\hat{\gamma}_2\)则会随\(\omega\)的取值发生变化（b随\(\omega\)同步变化）。

一个是y轴上的长度，一个是x轴上的长度，只在\(\omega=1\)时二者相等。

再看看二维输入的情况

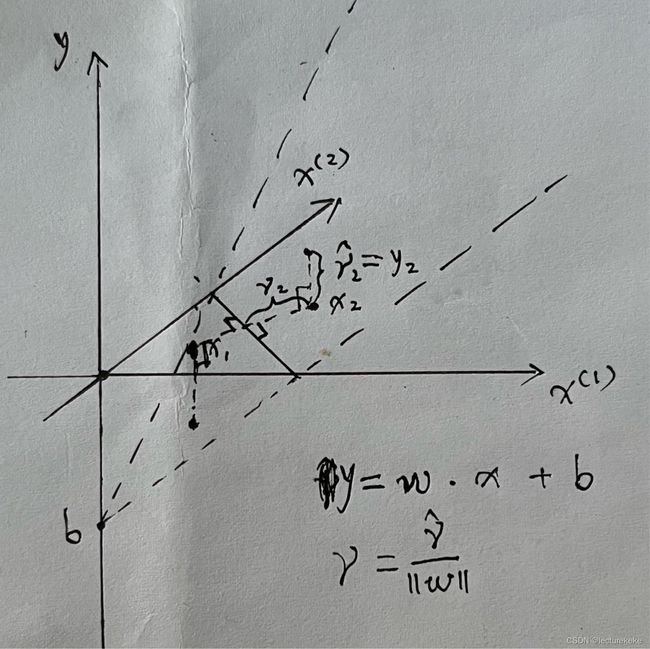
二维输入的函数图像需要在三维坐标系中表现。如上图所示，输入\(x\)为\(x^{(1)}\)和\(x^{(2)}\)二维空间上的点。输入与输出共同构成三维空间的函数的曲面（在这里为一个与y轴相交于b点的倾斜平面，\(x^{(1)}\)轴与\(x^{(2)}\)轴构成的平面与该平面相交线就是支持向量机的超平面），例如\(x_2\)在这个平面上对应的点可记作\(x{_2}\)'(\(x{^{(1)}_2},x{^{(2)}_2},y_2\))。

\(\gamma_2\)不一定等于\(\hat{\gamma}_2\)。当\(||\omega||=1\)时，二者相等。

同样三维输入的函数为四维图像，不过就无法做图，高维度输入向量原理同上。

结论：

函数间隔与几何间隔不相等，归根结底是由于二者的长度不在一个维度上。