遗传算法解决TSP问题
一、背景
遗传算法是基于自然选择和自然遗传机制的一种随机搜索算法,具有良好的并行性和全局寻优能力,能够自适应地调整搜索方向。这是一种相对来说比较简单的算法,因为它不需要问题求解者具备非常完备的问题领域知识,它能够通过类似生物体繁殖后代的机制自动生成问题的解,不过这个解往往不是该问题的最优解,而是相对来说的次优解。正是由于遗传算法简单的算法思路以及强大的搜索能力,它在机器人寻路、函数优化以及组合优化等诸多领域都得到了相当广泛的应用。用遗传算法求解旅行商问题就是遗传算法应用到组合优化问题中的一个经典例子。
二、旅行商问题
旅行商问题的目的是求解最优线路,是一类经典的规划类问题。旅行商问题是指,一个旅行商,要去往 n个不同的城市,需要每个城市都去,并且仅仅去一次,再回到最初的城市,形成一个环路,从众多可能路径中求解出一个最短的路径。旅行商问题是一个N完全问题,其所有的路线 数的搜索空间随着城市数 n的增大而快速增大,就产生了所谓的 “组合爆炸 ”问题。
旅行商问题的数学模型为:假设有 n 个( n 为有限正自然数)城市集合C={ 1,2,…,i,j,…,n } ;其中两城市间的距离为d_{ij}∈Z + ,其中的 i,j∈C(1≤i,j≤n);求解一个城市的序列 I(1),I(2),…,I(n) 使得使得从一个城市出发,遍历所有城市后又回到原城市的总路程最小时的。这里的 I(1),I(2),…, I(n)是城市序号 1,2,…,n 的一个全排列。根据上面的分析,可以得到的数学模型为:
min\sum_{i≠j}d_{ij}x_{ij}\qquad
s.t\sum_{i≠j}^nx_{ij} = 1,i = 1,2,…,n
\sum_{j= 1}^nx_{ij }= 1,j = 1,2,…,n
\sum_{i,j∈C}x_{ij}≤|C|-1,2≤ |C| ≤n - 2,C∈{1,2,…,n}
x_{ij}∈ {0,1} ;i = j = 1,2,…,n;i≠j
三、遗传算法
遗传算法是模拟自然进化过程来搜索全局最优解的方法。从一组随机生成的初始解(称为种群)开始搜索过程。其中每一个在种群内的个体都称为染色体(个体),它可以是多种不同的编码形式,现实意义代表着问题的一个解。在种群的繁衍过程中染色体会被遗传到子代中并在遗传过程中发生一些变异。在每一代种群中,适应度被用来衡量度个体的质量。下一代染色体被称为后代。后代是通过上一代染色体的杂交或变异而形成的。在形成新一代的过程中,将根据后代适应度的大小进行筛选,一些适应度较小的将被淘汰,以便保持种群规模不变。适应度高的染色体被选择的概率较高,经过有限次迭代后,算法收敛到最佳染色体。
1.种群初始化
生成顺序为1到city_num,长度为city_num的染色体,打乱该染色体的排列顺序。重复individual_num遍,组成初始种群。
2.编码
本实验采用路径表示编码方式,路径表示是 TSP 的自然、直观的表示方式。染色体中基因的值表示城市,基因的顺序表示访问城市的顺序,将基因顺序作为染色体的编码。在个体的染色体中,不允许有重复的基因编码,满足了任一个城市必须而且只能访问一次的约束。
程序中最初建立了一个 city_num*2 的矩阵,每一行代表一个城市的x轴、y轴坐标。每一个城市都有一个 1 到 city_num之间的数字的编号,这些编号的顺序作为染色体的编码。
3.交叉
交叉算子在遗传算法中起着核心的作用,它是指将个体进行两两配对。本实验使用的是部分映射交叉,如前面所述,路径表示的编码方法要求任一个城市必须而且只能访问一次,基本遗传算法的交叉操作生成的个体一般不能满足这一约束条件。为此本实验使用的部分映射交叉法在进行两点的简单交叉后,使用修复程序,是后代合法化。具体步骤如下
(1)随机抽取两个个体
(2)随机选取两个index1和index2。由两点定义的子串称为映射段。记录初始基因片段位置
(3)交换双亲的子串,形成原始后代。
(4)根据映射关系,将原始后代合法化。
4.变异
求解 TSP 时,变异算子的设计要比交叉算子的设计灵活的多,任何具有局部搜索功能的算子都可作为它的变异算子。本实验使用反转变异法,具体步骤如下
(1)按照变异概率=0.25选出变异个体
(2)随机选取两个index1和index2。由两点定义一个子串
(3)将子串中的城市顺序进行反转
5.适应度函数
适应性度是用来衡量一个可能解的好坏的度量标准,遗传算法参照适应度来选择后代。本实验选择个体解码后旅行城市路径长度,作为个体的适应度。
6.选择
在看论文的过程中看到了一种新的选择方法—竞标赛选择法,可以直接将根据适应度值对个体进行选择。所以本实验采用竞标赛选择法,每次从种群中取出一定数量个体组成一个小队,然后选择其中最好的一个进入子代种群。具体步骤如下
(1)从种群中随机选择10个个体组成一个小组
(2)使用冒泡排序法选出适应度值最大的个体加入种群
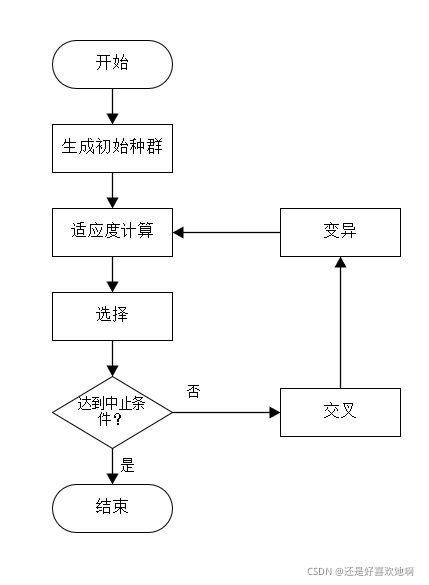
四、程序流程
五、原始数据及分析
本实验采用TSPLIB数据库对遗传算法进行测试,为保证实验的可靠性,采用遗传算法针对TSPLIB标准库中的eil51和eil101连续进行20次仿真。实验结果如下
| 问题 | 迭代次数100 | 迭代次数500 | 迭代次数1000 | 迭代次数2000 | 迭代次数5000 |
|---|---|---|---|---|---|
| eil51-avg | 869.61 | 547.69 | 462.13 | 445.33 | 440.74 |
| eil51-opt | 836.15 | 479.06 | 429.81 | 430.68 | 428.90 |
| eil101-avg | 2185.79 | 1312.10 | 1010.99 | 796.89 | 708.96 |
| eil101-opt | 2055.62 | 1254.77 | 957.62 | 764.84 | 685.17 |
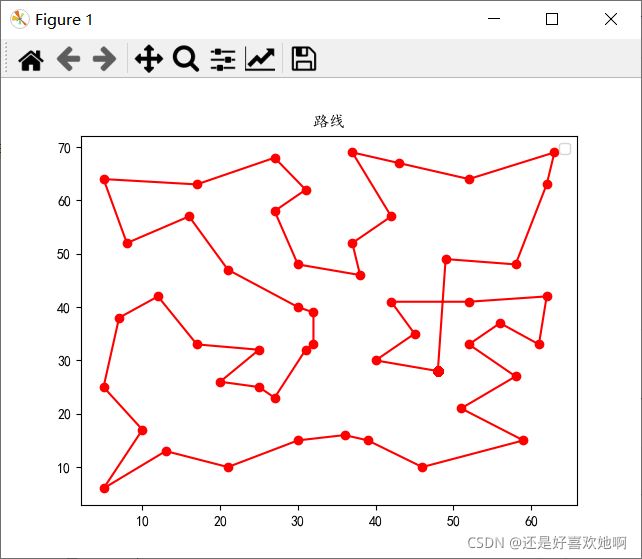
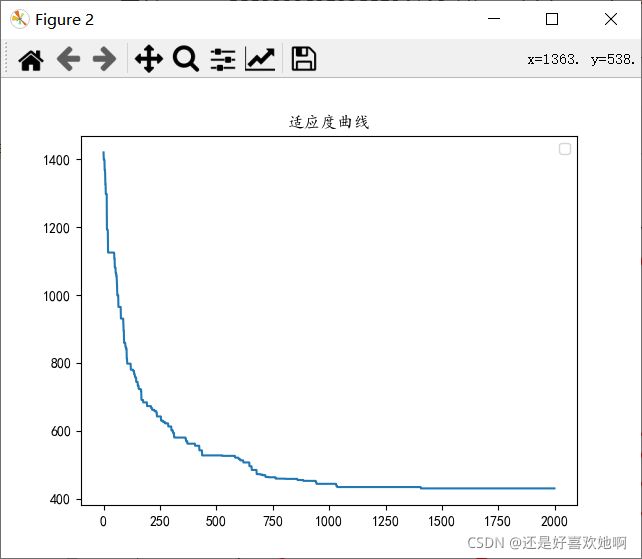
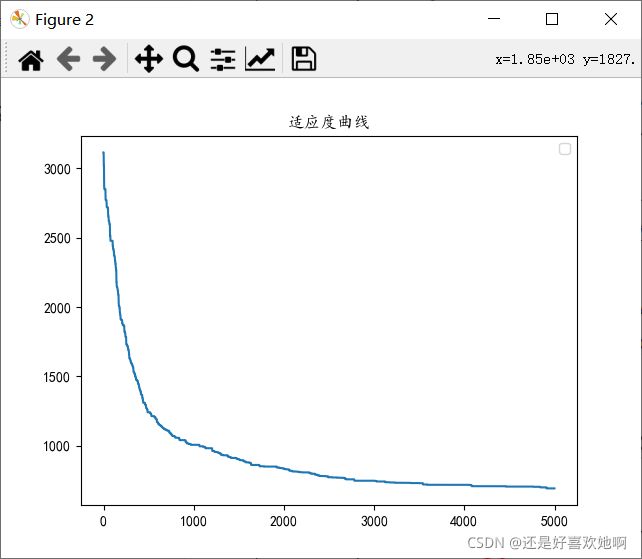
对于eil51问题,迭代次数为1500次左右时适应度曲线收敛,20次实验总路径长度平均值为445.33451306670287,最优值为430.681290988851,与TSPLIB中eil51最优解426相差较小。迭代2000次时的最优路径为[34, 35, 19, 2, 27, 30, 7, 25, 6, 42, 23, 22, 47, 5, 26, 50, 45, 11, 46, 3, 17, 13, 24, 12, 40, 39, 18, 41, 43, 16, 36, 14, 44, 32, 38, 9, 29, 33, 8, 49, 20, 28, 1, 21, 0, 31, 10, 15, 37, 48, 4, 34]。下图为最优路线及其适应度曲线
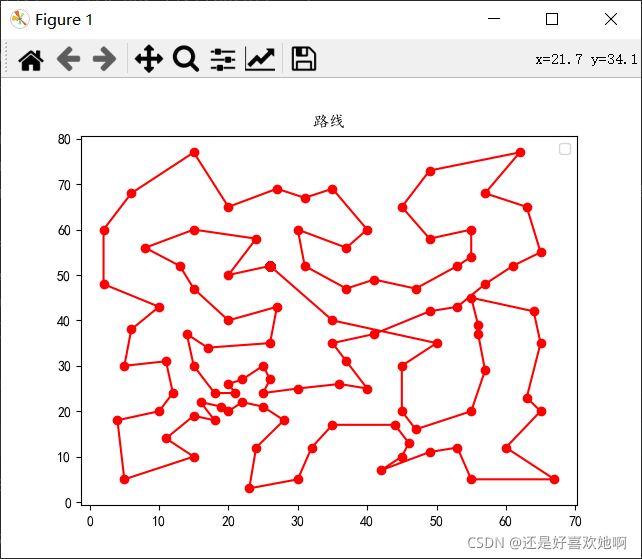
对于eil101问题,迭代次数为5000左右时适应度曲线收敛,20次实验总路径长度平均值为708.9668424017993,最优值为685.1710512581108,与TSPLIB中eil101最优解629相差不大。迭代次数为5000时,最优路径为[87, 6, 61, 18, 46, 47, 81, 17, 51, 88, 59, 82, 4, 92, 58, 98, 95, 5, 93, 94, 12, 57, 39, 52, 100, 27, 75, 76, 78, 77, 33, 34, 70, 64, 65, 19, 50, 8, 80, 32, 49, 0, 68, 30, 9, 69, 29, 31, 89, 62, 10, 63, 48, 35, 45, 7, 44, 16, 83, 60, 15, 85, 37, 13, 43, 90, 99, 84, 97, 36, 91, 96, 86, 41, 42, 14, 56, 1, 72, 73, 21, 40, 74, 55, 22, 66, 38, 24, 54, 23, 28, 2, 67, 79, 53, 3, 71, 20, 25, 11, 26, 87]
六、结论
通过运用遗传算法对上面两个问题(eil51和eil101)求解结果可以看出,运用遗传算法能够求解旅行商问题。对于同一个问题,随着迭代次数的增多,所得到的解越来越好。但当增加到某一值时,适应度函数会收敛并趋于平缓(这时可以认为达到了最优解)。
对于不同问题,当城市数量比较多时,需要的迭代搜索的次数就越多,求解完成需要的时间越长。使用遗传算法求解旅行商问题,理论上只要迭代次数足够多,就能够无限接近最优解。但是由于计算机算力限制,所以应该采用合适的交叉变异方法使用尽可能少的迭代次数,求得最优解的近似解。
七、展望
因为本次实验时间有限,只分析了遗传算法对于TSPLIB标准库中eil51个eil101两个问题在不同迭代次数时解的情况。其实遗传算法不同的交叉变异和选择方法对于算法性能的影响较大,如果后续从事相关研究,可以尝试使用控制变量法研究使用不同交叉变异和选择方法对算法性能的影响。