【论文精读】 使用空间梯度和噪声分割标签（伪标签）的深度学习配准

Deep learning based registration using spatial gradients and noisy segmentation labels

Théo Estienne, et al. “Deep Learning-Based Registration Using Spatial Gradients and Noisy Segmentation Labels.” MICCAI 2020

Abstract

Image registration is one of the most challenging problems in medical image analysis. In the recent years, deep learning based approaches became quite popular, providing fast and performing registration strategies. In this short paper, we summarise our work presented on Learn2Reg challenge 2020. The main contributions of our work rely on (i) a symmetric formulation, predicting the transformations from source to target and from target to source simultaneously, enforcing the trained representations to be similar and (ii) integration of variety of publicly available datasets used both for pretraining and for augmenting segmentation labels. Our method reports a mean dice of 0.64 for task 3 and 0.85 for task 4 on the test sets, taking third place on the challenge.

code

• https://github.com/TheoEst/abdominal_registration
• https://github.com/TheoEst/hippocampus_registration

---

配准

医学图像配准已经被研究很久了，这个问题依赖于找到一个合适的变形场来扭曲一个图像到另一个图像上，使它们结构上的相同部位尽可能重叠。即，给定一个浮动图像（moving image）$I_M$ 和一张固定图像（fixed image）$I_F$。预测一个位移场（displacement field）$u$，进而得到变形场（deformation field）$\Phi$，即从浮动图像到固定图像的映射，使得配准后的浮动图像（warped image）$I_W=I_M\circ \Phi$ 和固定图像尽可能相似。其中像素位置的变换可以表示为 $\Phi (x)=x+u(x)$。浮动图像又称源图像（source image），固定图像又称参考图像（reference image）、模板图像（template image），变形场又称流场（flow field）、配准场（registration field）、转换（transformation）¹。

介绍

随着深度学习的发展，许多基于深度学习的配准方法变得非常流行，提供了非常有效和先进的性能。尽管深度学习在图像配准领域已经做了很多工作，仍然有很多挑战需要解决。为了应对这些挑战，并为基于学习和传统方法的基准测试提供通用数据集，组织了 Learn2Reg 挑战。

主办方提出了四个 Tasks，各有不同的器官和模态。在这项工作中，我们集中在患者间（ inter-patient）² 的两个配准任务：

• 腹部 CT（Task 03）：这项任务的目的是在病人间配准腹部 CT 扫描。
• 海马体 MRI 配准（Task 04）：这项任务是将海马体的头部和身体对齐，以便患者间的比较。

在这项工作中，我们的深度神经网络学习如何以类似于^{3 4} 的方式获得空间梯度（spatial gradients $\nabla \Phi$），而不是直接输出变形场（deformation field $\Phi$）。

为了对变形部分进行建模，一种简单而直接的方法是为每个输出体素生成采样坐标，我们可以让网络直接计算这些采样点。然而，这样的选择需要网络生成具有值范围更大的特征图，这会使训练复杂化。此外，如果没有适当的正则化，可能会产生不平滑甚至不连续的变形。为了规避这个问题，我们采用⁵ 提出的方法并预测变形沿每个维度的空间梯度 Φ 而不是变形场本身。空间梯度 Φ 测量连续像素的位移，通过强制这些位移具有正值并随后沿每个维度应用积分操作，可以检索空间采样坐标。

这项工作的主要贡献在于：

• 使用相同的网络来预测两个变形场：${\Phi }_{M\to F}$ 和 ${\Phi }_{F\to M}$，由于使用了相同的编码器，这隐式地表现了其对称性（symmetric）；
• 充分利用公开可用的数据集在训练期间加入来自不同器官的噪声标签（伪标签）。

方法

我们的方法是基于这篇文章：Deep Learning-Based Concurrent Brain Registration and Tumor Segmentation， 2020 年 5 月，我们发表在 4 区期刊《Frontiers in Computational Neuroscience》上。

这是我对该文章的精读笔记：【论文精读】DL-Based 脑部医学图像双任务：联合配准和肿瘤分割

我们使用 3D Unet 作为 backbone，有 3 类损失函数：

• Reconstruction loss（均方差 MSE Loss 或局部互相关 Local-CC Loss）
• Segmentation loss（变形后的分割标签和 ground truth 分割标签之间的 Dice Loss）
• Regularisation loss（保证变形场的平滑）

• 编码器（E）

  网络的 backbone 是 3D-UNet，编码器部分（E）有四个 blocks，通道数分别为 64，128，256，和 512。每个 block 由一个 norm 层、Leaky-ReLU激活层、内核大小为 3 × 3 × 3 的 3D 卷积以及大D小为 2 的 stride 组成，以降低空间分辨率。每个固定、浮动图像独立地通过网络的编码器部分。

• 解码器（D）

  在通过解码器部分（D）之前使用减法运算融合浮动图像和固定图像的编码。（论文中没讲，merge 这步操作只在配准解码器前进行，分割解码器不需要 merge，因为浮动图像和固定图像是分别分割）

  解码器预测的是空间梯度（spatial gradients）$\nabla \Phi$，并计算对应的变形场（deformation field）$\Phi$。我们用累积求和运算近似积分来从其空间梯度 $\nabla \Phi$ 获得变形场 $\Phi$。然后使用 $\Phi$ 来变形浮动（固定）图像及其分割出来的伪标签（ground truth）：$M^{\text{warp }}=\mathcal{W}\left(M,{\Phi }_{M\to F}\right)$。最后，我们应用深度监督以类似于 ⁶ 的方式训练我们的网络。

  深度监督（Deep supervision）：利用多尺度估计和归一化损失函数提高配准性能。说人话就是使用多个不同的损失函数来训练。说真的计算机论文怎么这么爱炒概念，这不得不说也是严重内卷的一种现象。

• 对称训练（Symmetric training）

  尽管我们的网格公式（grid formulation）对空间梯度有限制，以避免 x、y、z 轴在垂直和水平方向上的自交叉（self-crossings），但我们的公式还不是同胚（diffeomorphic）的，这意味着我们无法计算 ${\Phi }_{M\to F}$ 的逆变换 ${\Phi }_{F\to M}$。为了解决这个问题，我们选择全部通过预测来得到 ${\Phi }_{M\to F}$ 和 ${\Phi }_{F\to M}$，并把它们加入到网络训练优化的损失函数中。由于我们在编码器部分的融合策略，我们的方法能够用较少的参数学习两种变换。

  我们的空间梯度 $\nabla \Phi$ 是通过以下方式获得的：
  $$\nabla {\Phi }_{M\to F}=\mathbf{D}(\mathbf{E}(M)-\mathbf{E}(F))，以及，\nabla {\Phi }_{F\to M}=\mathbf{D}(\mathbf{E}(F)-\mathbf{E}(M))$$

  总的来说对称训练就是同一个网络同时预测 ${\Phi }_{M\to F}$ 和 ${\Phi }_{F\to M}$（把它当成双任务学习，对称就是两个任务看起来是互逆的），然后把每个任务的 3 类损失函数加起来，总共 6 个损失函数相加进行总的反向传播。至于这样做的合理性，作者在实验结果部分给出了消融实验证实是有不错的效果的。

• 预训练和伪标签

  实验证明，在训练过程中，基于学习的配准方法结合了内隐解剖学知识，提高了配准效果。基于这个原因，在这项研究中，我们使用了公开可用的数据集（KITS 19，Medical Segmentation Decathlon（sub-cohort Liver, Spleen, Pancreas, Hepatic Lesion and Colon）and TCIA Pancreas）来提高神经网络的性能。

  特别地，我们指定了 11 个器官来训练一个也是基于 3D-UNet 的分割网络，目标是预测补充数据的分割标签，并将其当作伪标签用于配准的预训练。为了协调每个数据集的信息，我们使用修改后的 dice loss 来训练我们的网络，这样我们只反向传播 11 个器官的损失。

  下图来自作者的那篇文章：Deep Learning-Based Concurrent Brain Registration and Tumor Segmentation。

  通过这个图我们可以更加直观地看出分割网络的实现，其实就是双任务网络，分割和配准任务是独立的两个头，分割的结果（伪标签）会被用到配准网络的训练中去。
  
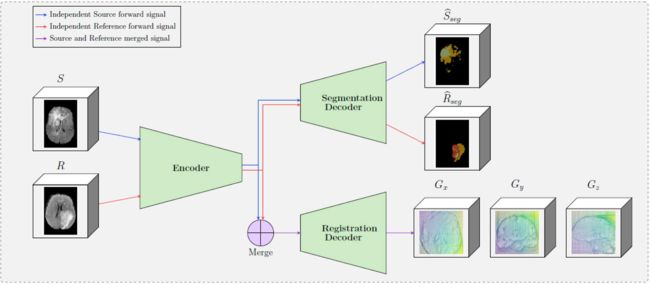
  在使用 ANTs 进行仿射配准步骤和进行 2mm 体素间距的各向同性重采样（isotropic resampling to 2mm voxel spacing）等小的预处理之后，补充数据和它们的分割标签（伪标签）将被用于 Task 03 的配准网络的预训练。

  此外，对于 Task 04，我们使用来自 OASIS3 数据集的大约 750 个 T1 MRI 进行了无监督的预训练，没有使用分割标签。对于这两项任务，预训练进行了 300 个 epochs。

训练策略和实现细节

为了训练我们的网络，我们使用了多个损失函数的组合（所谓深度监督，Deep supervision）。

• 图像相似性损失：$L_{recon}$

  第一个是重建损失（reconstruction loss），优化衡量两个图像灰度相似性的损失函数 $L_{recon}$。在我们的实验中，我们使用均方差函数和归一化互相关，计算变形图像 $M^{warped}$ 和固定图像 $F$ 之间的体素值相似度。

• 分割标签的 dice loss：$L_{seg}$

  第二个损失函数是通过优化变形后的浮动图像的分割标签和固定图像的分割标签之间的 dice 系数来整合解剖学知识：${\mathcal{L}}_{seg}=\mathrm{Dice}\left(M_{seg}^{\mathrm{warp}},F_{seg}\right)$。

• 位移场平滑度损失：$L_{reg}$

  整合了正则化损失，以加强位移场的平滑度：${\mathcal{L}}_{reg}=\Vert \nabla {\Phi }_{M\to F}\Vert$。

这些损失函数整合起来，构成了预测最佳 $\nabla {\Phi }_{M\to F}$ 和 $\nabla {\Phi }_{F\to M}$ 的最终优化策略：

$$\mathcal{L}={\left(\alpha {\mathcal{L}}_{recon}+\beta {\mathcal{L}}_{seg}+\gamma {\mathcal{L}}_{reg}\right)}_{M\to F}+{\left(\alpha {\mathcal{L}}_{recon}+\beta {\mathcal{L}}_{seg}+\gamma {\mathcal{L}}_{reg}\right)}_{F\to M}$$

α, β 以及 γ 是自定义的权重。使用 Adam optimiser 对网络训练进行优化，学习速率设置为 $1e^{-4}$。

• Task 03

  设置 batch size 为 2，限于显存的原因，使用 patch size 为 144×144×144。归一化策略包括三个 CT 窗口的提取，所有这些窗口都用作附加通道，并且 min-max 归一化到范围（0,1）内。对于 Task 03，我们没有使用任何数据增强，我们设置 α = 1，β = 1和 γ = 0.01。使用两张 V100 显卡跑了 300 个 epochs，花了大约 12 个小时。

• Task 04

  设置 batch size 为 6，限于显存的原因，使用 patch size 为 64×64×64。对于 Task 04 的少量原数据，我们通过随机翻转，随机旋转和转化（random flip, random rotation and translation）来进行数据增强。归一化策略包括：$\mathcal{N}(0,1)$ 归一化，把值在范围 [-5, 5] 外的剪切掉，min-max 到范围（0,1）内。我们设置 α = 1，β = 1和 γ = 0.01。使用两张 GTX 1080 显卡跑了 600 个 epochs，花了大约 20 个小时。

• 分割网络

  用于生成伪标签的分割网络使用 3D-UNet，batch size 设为 6，学习率为 $1e^{-4}$，激活函数使用 Leaky-ReLU，使用 instance normalisation 归一化层，随机裁剪出大小 144×144×144。在预测分割标签过程中，只要有的，我们都使用 ground truth 分割标签。

实验结果

对于每项任务，我们都进行了消融实验，以评估每个成分的贡献。我们的方法分别需要 6.21 秒和 1.43 秒来完成 Task 03 和 Task 04 的配准。这比其他 Learn2Reg 的参与者要慢，可能是因为我们的深度网络有大约 2000 万个参数（有点大啊）。

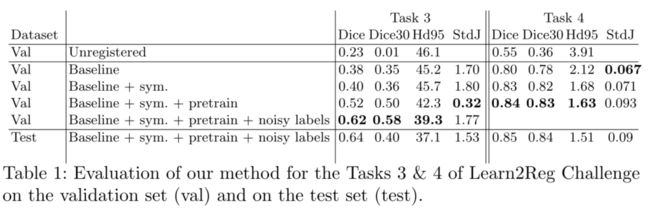
关于 Task 03，我们可以观察到，当使用伪标签进行预训练时，效果显著提高，从0.52 提升到 0.62。但是对称训练的促进效果则没有这么好，只从 0.38 提升到 0.40。

另一方面，对于 Task 04，预训练 + 对称训练增强了方法的鲁棒性，但影响程度比 Task 03 小。

结论

在这项工作中，我们总结了在 Learn2Reg 挑战赛中获得第三名的方法，我们参与了 Task 03和 Task 04。我们的公式基于空间梯度，探讨了对称性、预训练和公共可用数据集的伪标签造成的影响。在未来，我们的目标是在我们的方法中进一步探索对称性，并探讨我们的公式能够保持微分同胚性质的方法。最后，对抗性训练也是我们要探讨的问题，以便处理多模态配准。（对抗性训练是啥呀，他那篇文章的结论也提到了这个未来计划）

---

1. 棉花糖 - 基于深度学习的单模医学图像配准综述（附VoxelMorph配准实例） ↩︎

2. 患者自身 intra-patient，患者间 inter-patient。 ↩︎

3. Christodoulidis, Stergios et al. “Linear and Deformable Image Registration with 3D Convolutional Neural Networks.” RAMBO+BIA+TIA@MICCAI (2018). ↩︎

4. Théo Estienne, Marvin Lerousseau, et al. “Deep Learning-Based Concurrent Brain Registration and Tumor Segmentation.” Frontiers in Computational Neuroscience 14 (2020). https://doi.org/10.3389/fncom.2020.00017. ↩︎

5. Shu, Z., Sahasrabudhe, M., G¨uler, R.A., Samaras, D., Paragios, N., Kokkinos, I.:Deforming Autoencoders: Unsupervised Disentangling of Shape and Appearance.2018 IEEE European Conference on Computer Vision (ECCV) (2018) ↩︎

6. Julian Krebs, Herv´ e Delingette, Boris Mailh´ e, Nicholas Ayache, and TommasoMansi. Learning a probabilistic model for diffeomorphic registration. IEEE Transactions on Medical Imaging, 38(9), 2019. ↩︎