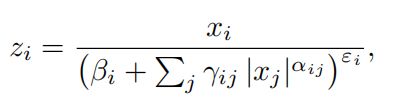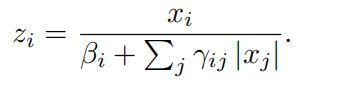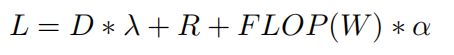阅读笔记:《Computationally Efficient Neural Image Compression》
《Computationally Efficient Neural Image Compression》
Nick Johnston, Elad Eban, Ariel Gordon, Johannes Ballé
Google Research
论文连接:https://arxiv.org/pdf/1912.08771.pdf
代码链接:暂未公开源码
摘要
这篇是Balle大神挂名关于神经网络图像压缩的计算效率研究的文章。目前在率-失真性能达到最好效果的深度学习图像压缩模型在计算量上还是一大挑战,作者分析解码器在运行时的复杂性,使用自动网络优化技术来降低神经图像压缩模型的计算复杂度,并在失真评价指标、率-失真表现以及运行时间之间达到平衡,同时作者设计并研究了有效计算的神经图像压缩模型。
本文的主要工作如下:
- 分析图像压缩框架(balle压缩模型)中解码器的计算复杂度;
- 在表现没有损失的情况下优化GDN激活函数;
- 采用一种正则化方法来优化解码器结构的有效计算的神经图像压缩模型(Computationally Efficient Neural Image Compression Models, CENIC),主要就是依据Group Lasso Reguarization来通过MorphNet[1](也是Google开源的一种深度学习网络模型优化的方法)来优化原有的解码器结构,使得优化后的解码器结构更简洁、计算效率更高同时不影响解码器的率失真性能;
- 依据率失真表现来平衡这些可学习的结构;
文章中图像压缩模型的baseline结构
baseline(如图1所示)结构也称为Mean-Scale Hyperprior network,其编解码器的参数配置如表1所示,但是网络中去掉了上下文模型(context model),去掉的原因有两个:
1:要求baseline测试的简洁性,并且baseline结构的性能已经优于BPG了;
2:对于实现隐含特征有效计算的自回归上下文模型很困难;
图1 baseline的编解码网络结构(不包含上下文模型)
表1 Mean-Scale Hyperprior Network的参数配置
因为组套索正则化(Group Lasso Regularization)可以从网络结构中删除作用冗余的通道,而且了解到在整个学习到的最终结构中的计算量较少,所以我们从一个过度参数化的网络开始。基于图1 的编解码模型结构,作者定义参数过度的网络称为Larger Mean-Scale Hyperprior Network,其参数配置如表2所示,经由MorphNet方法优化学习后得到的最终结构称为Computationally Efficient Neural Image Compression model。
表2 Larger Mean-Scale Hyperprior Network的参数配置
GDN激活函数
GDN作为一个概率流模型,它的定义如下:
其中![]() 是输入向量,
是输入向量,![]() 是输出向量,
是输出向量,![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别为可训练的参数,i和j是通道的索引。在自编码风格的图像压缩模型中,实验证明在相同数量的隐藏单元下,相对于常规的激活函数relu和tanh,GDN可以产生更好的表现。同样在baseline中使用GDN作为激活函数。为了简化有论文固定一些参数(
分别为可训练的参数,i和j是通道的索引。在自编码风格的图像压缩模型中,实验证明在相同数量的隐藏单元下,相对于常规的激活函数relu和tanh,GDN可以产生更好的表现。同样在baseline中使用GDN作为激活函数。为了简化有论文固定一些参数(![]() =2,
=2, ![]() =0.5),而鉴于计算平方根需要更多循环计算,我们发现
=0.5),而鉴于计算平方根需要更多循环计算,我们发现![]() =
=![]() =1并不影响效果当去掉计算平方根的需要,简化后的GDN的计算方式如下:
=1并不影响效果当去掉计算平方根的需要,简化后的GDN的计算方式如下:
实验证明去掉了平方根运算后,模型的PSNR表现不受影响。
由Group Lasso Regularization训练
针对前面所说的参数过度的Larger Mean-Scale Hyperprior模型存在参数冗余,作者采用MorphNet对参数过度的模型进行训练和学习,由于Mean-Scale Hyperprior模型没有使用批归一化(BatchNorm)操作,作者便采用加权的Group Lasso Regularization项。
对于矩阵W和n输出的全连接层,正则项定义为:
其中![]() 代表第j个输出相关的所有权重。类似地,这也适用于卷积。
代表第j个输出相关的所有权重。类似地,这也适用于卷积。
实验中,FLOP-regularizer的阈值设为0.001来决定激活哪一个输出,按照MorphNet的流程,首先通过使用增加的正则化强度来学习几种结构,然后在结构收敛之后,根据给定的学习好的结构重新训练模型。在这两个阶段之间不存储任何checkpoint或重复使用任何权重,而且第二阶段的训练是从头开始。
对于训练的设置:
Model:Larger Mean Scale model architectures
Learning Rate: 1e-4
Optimizer: Adam(β1=0.9,β2=0.999, ε=1e8)
除了训练通常的率-失真损失项外,对训练的第一遍进行了修改,以包括针对FLLOP(W)表示的解码器和超解码器中的权重的FLOP-regularizer。损失约束为:
对于失真损失D,当D为MSE时,lambda可取的值为:
当D为MSSSIM时,lambda可取的值为:
而对于alpha,不论失真损失是哪一种,alpha可取的值为:
在第一个阶段,这些模型大概训练100K步,通过对lambda和alpha的扫描可以创建207个唯一的解码器结构。
在第二个训练阶段,我们将解码器中的卷积滤波器减小到由FLOP正则化器确定的值,并进行1e6步以上的训练或收敛。
文章对实验进行了详细的分析,包括baseline与Larger Mean-Scale Hyperprior之间的PSNR,MSSSIM的分析,GDN激活函数的表现,CENIC结构的表现, CPU与GPU之间的差异表现等等,具体的细节详见论文。
结论
首先,在探索FLOP正则化架构的过程中,我们发现仅向每层添加更多容量(比如卷积核的数量)不会带来额外的速-失真增益。 这导致我们得出以下结论:这些四层解码器和三层超解码器网络已经针对高速率失真性能进行了很好的调整,尤其是在频谱的高比特率/高质量端,并且这样做在运行时间和训练时间上需要更高的成本。
其次,我们发现在将网络限制为特定运行时间的同时,自动进行架构搜索以及使用诸如MorphNet之类的方法可以直接在FLOP上进行优化非常重要,因为超参数搜索空间太大,无法手动有效地找到好的架构。
模型对CPU和GPU的比较表明,计算平台和实现至关重要。 在强大的GPU上运行,运行时间几乎提高了3倍。 针对MSE的优化还降低了跨两个平台的方差解码时间。 差异是由于神经网络编码和概率分布之间的复杂相互作用影响距离编码器的编码和解码时间,因为神经网络组件的计算量对于这些模型是固定的。
看完GDN激活功能后,我们还建议简化![]() 和
和![]() 参数以减少解码时间,同时还保持速率失真性能几乎相同。
参数以减少解码时间,同时还保持速率失真性能几乎相同。
最后,MS-SSIM优化模型比MSE优化模型更易于优化计算。 这是令人鼓舞的,因为MS-SSIM通常比MSE与人的感知质量更好地相关。 针对解码器速度进行优化不仅允许使用更实用,更快速的推理模型,而且由于参数较少且梯度较小,因此可以更快地进行神经网络训练。
[1] Ariel Gordon, Elad Eban, Ofifir Nachum, Bo Chen, Hao Wu, Tien Ju Yang, and Edward Choi. Morphnet: Fast & simple