pytorch 矩阵分解
We come across recommendations multiple times a day — while deciding what to watch on Netflix/Youtube, item recommendations on shopping sites, song suggestions on Spotify, friend recommendations on Instagram, job recommendations on LinkedIn…the list goes on! Recommender systems aim to predict the “rating” or “preference” a user would give to an item. These ratings are used to determine what a user might like and make informed suggestions.
我们每天都会遇到很多建议-在决定在Netflix / Youtube上观看什么,在购物网站上推荐商品,在Spotify上推荐歌曲,在Instagram上推荐朋友,在LinkedIn上推荐工作...等等! 推荐系统旨在预测用户对某项商品的“评价”或“偏好”。 这些评分用于确定用户可能喜欢的内容并提出明智的建议。
There are two broad types of Recommender systems:
推荐系统分为两种:
Content-Based systems: These systems try to match users with items based on items’ content (genre, color, etc) and users’ profiles (likes, dislikes, demographic information, etc). For example, Youtube might suggest me cooking videos based on the fact that I’m a chef, and/or that I’ve watched a lot of baking videos in the past, hence utilizing the information it has about a video’s content and my profile.
基于内容的系统 :这些系统尝试根据项目的内容(类型,颜色等)和用户的个人资料(喜欢,不喜欢,人口统计信息等)为用户匹配项目。 例如,Youtube可能会基于我是厨师和/或我过去看过很多烘焙视频的事实而建议我烹饪视频,从而利用其有关视频内容和个人资料的信息。
Collaborative filtering: They rely on the assumption that similar users like similar items. Similarity measures between users and/or items are used to make recommendations.
协同过滤 :他们基于类似用户喜欢类似项目的假设。 用户和/或项目之间的相似性度量用于提出建议。
This article talks about a very popular collaborative filtering technique called Matrix factorization.
本文讨论了一种非常流行的协作过滤技术,称为矩阵分解。
矩阵分解 (Matrix Factorization)
A recommender system has two entities — users and items. Let’s say we have m users and n items. The goal of our recommendation system is to build an mxn matrix (called the utility matrix) which consists of the rating (or preference) for each user-item pair. Initially, this matrix is usually very sparse because we only have ratings for a limited number of user-item pairs.
推荐系统具有两个实体-用户和项目。 假设我们有m用户和n项目。 我们的推荐系统的目标是构建一个mxn矩阵(称为效用矩阵 ),该矩阵由每个用户项对的评分(或偏好)组成。 最初,此矩阵通常非常稀疏,因为我们仅对有限数量的用户项对进行评级。
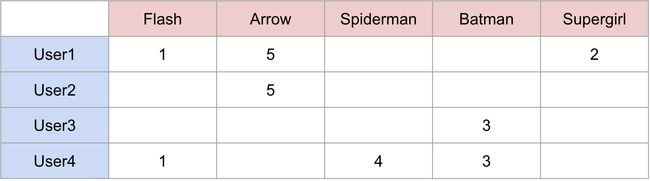
Here’s an example. Say we have 4 users and 5 superheroes and we’re trying to predict the rating each user would give to each superhero. This is what our utility matrix initially looks like:
这是一个例子。 假设我们有4个用户和5个超级英雄,我们正在尝试预测每个用户对每个超级英雄的评价。 这是我们的效用矩阵最初的样子:
4x5 utility matrix for superhero ratings (Image by author) 超级英雄评级的4x5实用矩阵(作者提供)Now, our goal is to populate this matrix by finding similarities between users and items. To get an intuition, for example, we see that User3 and User4 gave the same rating to Batman, so we can assume the users are similar and they’d feel the same way about Spiderman and predict that User3 would give a rating of 4 to Spiderman. In practice, however, this is not as straightforward because there are multiple users interacting with many different items.
现在,我们的目标是通过查找用户和项目之间的相似性来填充此矩阵。 例如,为了获得直觉,我们看到User3和User4对蝙蝠侠给予了相同的评分,因此我们可以假设用户相似并且他们对Spiderman的感受相同,并预测User3给予4的评分。蜘蛛侠。 但是,实际上,这并不是那么简单,因为有多个用户与许多不同的项目进行交互。
In practice, The matrix is populated by decomposing (or factorizing) the Utility matrix into two tall and skinny matrices. The decomposition has the equation:
在实践中,通过将Utility矩阵分解(或分解)为两个又高又瘦的矩阵来填充矩阵。 分解具有以下公式:
where U is m x k and V is n x k. U is a representation of users in some low dimensional space, and V is a representation of items. For a user i, uᵢ gives the representation of that user, and for an item e, vₑ gives the representation of that item. The rating prediction for a user-item pair is simply:
其中U是mxk ,V是nxk 。 U是某些低维空间中用户的表示,而V是项的表示。 对于用户i,uᵢ给出该用户的表示,对于项目e,vₑ给出该项目的表示。 用户项对的评级预测很简单:
PyTorch实施 (PyTorch Implementation)
To implement matrix factorization using PyTorch, we can use embedding layers provided by PyTorch for the user and item embedding matrices and use Gradient Descent to get the optimal decomposition. If you’re unfamiliar with embeddings, you can check out this article where I’ve talked about them in detail:
为了使用PyTorch实现矩阵分解,我们可以使用PyTorch为用户和项目嵌入矩阵提供的嵌入层,并使用Gradient Descent获得最佳分解。 如果您不熟悉嵌入,可以在我详细讨论嵌入的文章中查看:
码 (Code)
All the code I’ve used in this article can be found here: https://jovian.ml/aakanksha-ns/anime-ratings-matrix-factorization
我在本文中使用过的所有代码都可以在这里找到: https : //jovian.ml/aakanksha-ns/anime-ratings-matrix-factorization
数据集 (Dataset)
I’ve used the Anime Recommendations dataset from Kaggle:
我使用了Kaggle的Anime Recommendations数据集:
We have a total of 69600 users and 9927 anime. There are 6337241 ratings provided (out of 690,919,200 possible ratings).
我们共有69600用户和9927动漫。 提供了6337241个等级(可能的等级为690,919,200个)。
问题陈述 (Problem Statement)
Given a set of user ratings for anime, predict the rating for each user-anime pair.
给定一组动漫用户评级,预测每个动漫对的评级。
数据探索 (Data Exploration)
We see that there are lots of rows with a rating of -1 , indicating missing ratings, we can get rid of these rows.
我们看到有很多行的评分为-1 ,表示缺少评分,我们可以摆脱这些行。
We can also look at the distribution of ratings and number of ratings per user.
我们还可以查看评分的分布和每个用户的评分数量。
前处理 (Preprocessing)
Because we’ll be using PyTorch’s embedding layers to create our user and item embeddings, we need continuous IDs to be able to index into the embedding matrix and access each user/item embedding.
因为我们将使用PyTorch的嵌入层来创建用户和项目嵌入,所以我们需要连续的ID,以便能够索引到嵌入矩阵中并访问每个用户/项目嵌入。
训练 (Training)
Our goal is to find the optimal embeddings for each user and each item. We can then use these embeddings to make predictions for any user-item pair by taking the dot product of user embedding and item embedding
我们的目标是为每个用户和每个项目找到最佳的嵌入。 然后,我们可以通过获取用户嵌入和项目嵌入的点积,使用这些嵌入对任何用户项对进行预测
Cost function: We are trying to minimize the Mean squared error over the utility matrix. Here N is the number of non-blank elements in the utility matrix.
成本函数:我们正在尝试使效用矩阵的均方误差最小。 N是效用矩阵中非空白元素的数量。
Cost function for Matrix factorization 矩阵分解的成本函数 Prediction using item and user embeddings 使用项目和用户嵌入进行预测 MSE 微软Initializing user and item embeddings: There are many ways to initialize embedding weights and it’s an active area of research, for example, fastai uses something called Truncated Normal initializer. In my implementation, I’ve just initialized my embeddings with uniform values in (0, 11/K) (randomly, worked well in my case!) where K is the number of factors in the embedding matrix. K is a hyperparameter that’s usually decided empirically— it shouldn’t be too small because you want your embeddings to learn enough features but you also don’t want it to be too large as it can start overfitting to your training data and increase the computational time.
初始化用户和项目的嵌入 :初始化嵌入权重的方法有很多,这是一个活跃的研究领域,例如, fastai使用一种称为Truncated Normal初始化器的东西。 在我的实现中,我刚刚使用(0,11 / K)中的统一值初始化了嵌入(随机,在我的情况下效果很好!),其中K是嵌入矩阵中的因子数。 K是一个通常根据经验确定的超参数-不应太小,因为您希望您的嵌入学习足够的特征,但又不希望它太大,因为它可能会开始过度拟合您的训练数据并增加计算量时间。
Creating Sparse utility matrix: Since our cost function needs the utility matrix, we need a function to create this matrix.
创建稀疏效用矩阵:由于我们的成本函数需要效用矩阵,因此我们需要一个函数来创建此矩阵。
Gradient Descent:
梯度下降 :
The gradient descent equations are:
梯度下降方程为:
I’ve used momentum in my implementation which is a method that helps accelerate gradient descent in the relevant direction and dampens oscillations leading to faster convergence. I’ve also added regularization to ensure my model does not overfit to the training data. Hence, the gradient descent equations in my code are slightly more complex than the ones mentioned above.
我在实现过程中使用了动量,该动量可以帮助加速相关方向上的梯度下降并抑制振荡,从而加快收敛速度。 我还添加了正则化以确保我的模型不会过度适合训练数据。 因此,我的代码中的梯度下降方程比上述方程稍微复杂。
The regularized cost function is:
正则成本函数为:
Training 训练验证集预测 (Prediction on Validation Set)
Because we cannot make predictions for users and anime (cold start problem) we have not encountered in our training set, we need to remove them from our unseen dataset.
因为我们无法为我们的训练集中未遇到的用户和动漫(冷启动问题)做出预测,所以我们需要从看不见的数据集中删除它们。
Our model has slightly overfitted the training data, so the regularization factor (lambda) can be increased to make it generalize better.
我们的模型略微拟合了训练数据,因此可以增加正则化因子(lambda)以使其更好地泛化。
Let’s look at a few predictions:
让我们看一些预测:
Given that these ratings are based solely on similarities between user behaviors, a root mean square of just 3.4 in a rating range of 1–10 is pretty impressive. It shows how powerful matrix factorization can be even though it is so simple.
鉴于这些评分仅基于用户行为之间的相似性,在1-10的评分范围内,均方根值仅为3.4相当令人印象深刻。 它显示了即使如此简单,矩阵分解仍然具有多么强大的功能。
矩阵分解的局限性 (Limitations of Matrix Factorization)
Matrix factorization is a very simple and convenient way to make recommendations. However, it has its pitfalls, one of which we have already encountered in our implementation:
矩阵分解是一种非常简单方便的建议方法。 但是,它有其陷阱,在实现过程中我们已经遇到了其中之一:
冷启动问题 (Cold Start Problem)
We cannot make predictions for items and users we’ve never encountered in the training data because we don’t have embeddings for them.
我们无法对训练数据中从未遇到的项目和用户进行预测,因为我们没有针对它们的嵌入。
The cold-start problem can be addressed in many ways including Recommending popular items, Asking the user to rate some items, using a content-based approach until we have enough data to use collaborative filtering.
冷启动问题可以通过多种方式解决,包括推荐热门商品,要求用户对某些商品进行评分,使用基于内容的方法,直到我们有足够的数据来使用协作过滤。
难以包含有关用户/项目的其他上下文 (Hard to include additional context about user/item)
We only used user IDs and item IDs to create the embeddings. We are not able to use any other information about our users and items in our implementation. There are some complex hybrid models of content-based collaborative filtering that can be used to address this.
我们仅使用用户ID和商品ID来创建嵌入。 我们无法在实现中使用有关用户和项目的任何其他信息。 有一些基于内容的协作筛选的复杂混合模型可以用来解决此问题。
评级并非总是可用 (Ratings are not always available)
It’s hard to get feedback from users. Most users rate things only when they really like something or absolutely hate it. In such cases, we often have to come up with a way to measure implicit feedback and use negative sampling techniques to come up with a reasonable training set.
很难从用户那里获得反馈。 大多数用户仅在真正喜欢或绝对讨厌的情况下对事物进行评分。 在这种情况下,我们常常不得不想出一种方法来测量隐式反馈,并使用负采样技术来得出合理的训练集。
结论 (Conclusion)
Recommendation systems are really interesting but can also get too complex too easily, especially when implemented at scale where there are millions of users and millions of items. If you want to dive deeper into recommendation systems, check out various case studies — how Youtube recommends videos, LinkedIn job recommendations, Ad ranking. Often, you can find research papers/ videos/ engineering blogs corresponding to these case studies. Here are a few helpful resources:
推荐系统确实很有趣,但也可能太容易变得太复杂,尤其是在有数百万用户和数百万项的大规模实施时。 如果您想深入了解推荐系统,请查看各种案例研究-Youtube如何推荐视频,LinkedIn职位推荐,广告排名。 通常,您可以找到与这些案例研究相对应的研究论文/视频/工程博客。 以下是一些有用的资源:
https://engineering.linkedin.com/blog/2019/04/ai-behind-linkedin-recruiter-search-and-recommendation-systems
https://engineering.linkedin.com/blog/2019/04/ai-behind-linkedin-recruiter-search-and-recommendation-systems
https://static.googleusercontent.com/media/research.google.com/en//pubs/archive/45530.pdf
https://static.googleusercontent.com/media/research.google.com/en//pubs/archive/45530.pdf
https://labs.pinterest.com/user/themes/pin_labs/assets/paper/p2p-www17.pdf
https://labs.pinterest.com/user/themes/pin_labs/assets/paper/p2p-www17.pdf
翻译自: https://towardsdatascience.com/recommender-systems-matrix-factorization-using-pytorch-bd52f46aa199
pytorch 矩阵分解