Self-Ensembling For Visual Domain Adaptation

Self-Ensembling For Visual Domain Adaptation视觉域自适应的自封装

ABSTRACT

This paper explores the use of self-ensembling for visual domain adaptation problems. Our technique is derived from the mean teacher variant (Tarvainen & Valpola (2017)) of temporal ensembling (Laine & Aila (2017)), a technique that achieved state of the art results in the area of semi-supervised learning. We introduce a number of modifications to their approach for challenging domain adaptation scenarios and evaluate its effectiveness. Our approach achieves state of the art results in a variety of benchmarks, including our winning entry in the VISDA-2017 visual domain adaptation challenge. In small image benchmarks, our algorithm not only outperforms prior art, but can also achieve accuracy that is close to that of a classifier trained in a supervised fashion.
本文探讨了在视觉领域适应问题中使用自组装技术。 我们的技术源自时间合奏（Laine＆Aila（2017））的平均教师变体（Tarvainen＆Valpola（2017）），该技术在半监督学习领域取得了最先进的成果。 我们对他们的方法进行了许多修改，以应对具有挑战性的领域适应方案，并评估了其有效性。 我们的方法在各种基准测试中均达到了最先进的结果，其中包括我们在VISDA-2017视觉领域适应挑战赛中的获胜作品。 在小型图像基准测试中，我们的算法不仅优于现有技术，而且可以获得与以监督方式训练的分类器接近的精度。

INTRODUCTION

The strong performance of deep learning in computer vision tasks comes at the cost of requiring large datasets with corresponding ground truth labels for training. Such datasets are often expensive to produce, owing to the cost of the human labour required to produce the ground truth labels.
深度学习在计算机视觉任务中的强大表现是以需要具有相应地面真理标签的大型数据集进行训练为代价的。 由于产生地面真相标签所需的人工成本，这种数据集的生产成本通常很高。

Semi-supervised learning is an active area of research that aims to reduce the quantity of ground truth labels required for training. It is aimed at common practical scenarios in which only a small subset of a large dataset has corresponding ground truth labels. Unsupervised domain adaptation
is a closely related problem in which one attempts to transfer knowledge gained from a labeled source dataset to a distinct unlabeled target dataset, within the constraint that the objective (e.g.digit classification) must remain the same. Domain adaptation offers the potential to train a model using
labeled synthetic data – that is often abundantly available – and unlabeled real data. The scale of the problem can be seen in the VisDA-17 domain adaptation challenge images shown in Figure 1. We will present our winning solution in Section 4.2.
半监督学习是一个活跃的研究领域，旨在减少训练所需的地面真相标签数量。 它针对的是常见的实际情况，在这些情况下，大型数据集的仅一小部分具有相应的地面真相标签。 无监督域适应是一个密切相关的问题，其中人们试图在目标（例如数字分类）必须保持相同的约束下，将从标记源数据集获得的知识转移到不同的未标记目标数据集。 域自适应提供了使用标记的合成数据（通常是大量可用的）和未标记的真实数据来训练模型的潜力。 问题的严重程度可以从图1所示的VisDA-17域适应挑战图像中看出。我们将在第4.2节中介绍我们的获奖解决方案。

Recent work (Tarvainen & Valpola (2017)) has demonstrated the effectiveness of self-ensembling with random image augmentations to achieve state of the art performance in semi-supervised learning benchmarks.We have developed the approach proposed by Tarvainen & Valpola (2017) to work in a domain adaptation scenario. We will show that this can achieve excellent results in specific small image domain adaptation benchmarks. More challenging scenarios, notably MNIST -> SVHN and the VisDA-17 domain adaptation challenge required further modifications. To this end, we developed confidence thresholding and class balancing that allowed us to achieve state of the art results in
a variety of benchmarks, with some of our results coming close to those achieved by traditional supervised learning. Our approach is sufficiently flexble to be applicable to a variety of network architectures, both randomly initialized and pre-trained.
最近的工作（Tarvainen＆Valpola（2017））证明了在随机监督的学习基准中自组装和随机图像增强的有效性，以达到最先进的性能。 在域适应方案中工作。 我们将证明，在特定的小图像域自适应基准测试中，这可以取得出色的结果。 更具挑战性的场景，尤其是MNIST-> SVHN和VisDA-17域自适应挑战，需要进一步修改。 为此，我们开发了置信度阈值和类平衡，使我们能够在各种基准中获得最先进的结果，其中一些结果接近于传统的有监督学习所达到的结果。 我们的方法足够灵活，可以应用于随机初始化和预训练的各种网络体系结构。

Our paper is organised as follows; in Section 2 we will discuss related work that provides context and forms the basis of our technique; our approach is described in Section 3 with our experiments and results in Section 4; and finally we present our conclusions in Section 5.
我们的论文组织如下： 在第二部分中，我们将讨论相关的工作，这些工作提供了背景并构成了我们技术的基础。 我们的方法在第3节中进行了介绍，在第4节中介绍了我们的实验和结果； 最后，我们在第5节中提出结论。

RELATED WORK

In this section we will cover self-ensembling based semi-supervised methods that form the basis of our approach and domain adaptation techniques to which our work can be compared.
在本节中，我们将介绍基于自我组装的半监督方法，这些方法构成了我们的方法和领域自适应技术的基础，可以与我们的工作进行比较。
SELF-ENSEMBLING FOR SEMI-SUPERVISED LEARNING
Recent work based on methods related to self-ensembling have achieved excellent results in semisupervised learning scenarious. A neural network is trained to make consistent predictions for unsupervised samples under different augmentation Sajjadi et al. (2016), dropout and noise conditions
or through the use of adversarial training Miyato et al. (2017). We will focus in particular on the self-ensembling based approaches of Laine & Aila (2017) and Tarvainen & Valpola (2017) as they form the basis of our approach.
基于与自我组装相关的方法的最新工作在半监督学习场景中取得了优异的成绩。 训练了一个神经网络，以在不同的增强下对无监督样本做出一致的预测Sajjadi等（2016），辍学和噪声条件下或通过对抗训练使用Miyato等（2017）。 我们将特别关注Laine＆Aila（2017）和Tarvainen＆Valpola（2017）的基于自我集合的方法，因为它们构成了我们方法的基础。

Laine & Aila (2017) present two models; their Π-model and their temporal model. The Π-model passes each unlabeled sample through a classifier twice, each time with different dropout, noise and image translation parameters. Their unsupervised loss is the mean of the squared difference in class probability predictions resulting from the two presentations of each sample. Their temporal model maintains a per-sample moving average of the historical network predictions and encourages subsequent predictions to be consistent with the average. Their approach achieved state of the art
results in the SVHN and CIFAR-10 semi-supervised classification benchmarks.
Laine＆Aila（2017）提出了两种模型; 他们的Π模型和他们的时间模型。 Π模型将每个未标记的样本两次通过分类器，每次具有不同的滤失，噪声和图像转换参数。 它们的无监督损失是由每个样本的两次表示导致的类概率预测的平方差的均值。 他们的时间模型维持历史网络预测的每个样本移动平均值，并鼓励后续预测与平均值保持一致。 他们的方法在SVHN和CIFAR-10半监督分类基准中达到了最新水平。

Tarvainen & Valpola (2017) further improved on the temporal model of Laine & Aila (2017) by using an exponential moving average of the network weights rather than of the class predictions.Their approach uses two networks; a student network and a teacher network, where the student is trained using gradient descent and the weigthts of the teacher are the exponential moving average of those of the student. The unsupervised loss used to train the student is the mean square difference between the predictions of the student and the teacher, under different dropout, noise and image translation parameters.
Tarvainen＆Valpola（2017）通过使用网络权重的指数移动平均值而非类别预测对Laine＆Aila（2017）的时间模型进行了进一步改进。 学生网络和教师网络，其中使用梯度下降训练学生，而教师的权重是学生的指数移动平均值。 用于训练学生的无监督损失是在不同的辍学，噪声和图像翻译参数下，学生和老师的预测之间的均方差。
DOMAIN ADAPTATION
There is a rich body of literature tackling the problem of domain adaptation. We focus on deep learning based methods as these are most relevant to our work.
关于域适应问题的文献很多。 我们专注于基于深度学习的方法，因为这些方法与我们的工作最相关。

Auto-encoders are unsupervised neural network models that reconstruct their input samples by first encoding them into a latent space and then decoding and reconstructing them. Ghifary et al. (2016) describe an auto-encoder model that is trained to reconstruct samples from both the source and target domains, while a classifier is trained to predict labels from domain invariant features present in the latent representation using source domain labels. Bousmalis et al. (2016) reckognised that samples from disparate domains have distinct domain specific characteristics that must be represented in the latent representation to support effective reconstruction. They developed a split model that separates the latent representation into shared domain invariant features and private features specific to the source and target domains. Their classifier operates on the domain invariant features only.
自动编码器是无监督的神经网络模型，通过先将其编码到一个潜在空间中，然后对其进行解码和重构，从而重构其输入样本。 Ghifary等。 （2016年）描述了一种自动编码器模型，该模型经过训练可以从源域和目标域中重建样本，而分类器则可以通过使用源域标签根据潜在表示中存在的域不变特征来预测标签。 Bousmalis等人（2016）认识到，来自不同域的样本具有独特的域特定特征，必须在潜在表示中表示这些特征以支持有效的重建。 他们开发了一个拆分模型，将潜在表示分为源域和目标域专用的共享域不变特征和私有特征。 他们的分类器仅对域不变特征进行操作。

Ganin & Lempitsky (2015) propose a bifurcated classifier that splits into label classification and domain classification branches after common feature extraction layers. A gradient reversal layer is placed between the common feature extraction layers and the domain classification branch; while the domain classification layers attempt to determine which domain a sample came from the gradient reversal operation encourages the feature extraction layers to confuse the domain classifier by extracting domain invariant features. An alternative and simpler implementation described in their appendix minimises the label cross-entropy loss in the feature and label classification layers, minimises the domain cross-entropy in the domain classification layers but maximises it in the feature layers. The model of Tzeng et al. (2017) runs along similar lines but uses separate feature extraction sub-networks for source and domain samples and train the model in two distinct stages.
Ganin＆Lempitsky（2015）提出了一种分叉的分类器，该分类器在共有特征提取层之后分为标签分类和域分类分支。 梯度反转层位于公共特征提取层和域分类分支之间； 而领域分类层试图确定样本来自梯度反转操作的哪个领域，则鼓励特征提取层通过提取领域不变特征来混淆领域分类器。 在其附录中描述的另一种更简单的实现方式是将特征和标签分类层中的标签交叉熵损失最小化，将域分类层中的域交叉熵最小化，但将其在特征层中最大化。 Tzeng等人（2017）的模型沿相似的路线运行，但对源和域样本使用单独的特征提取子网，并在两个不同的阶段训练模型。

Saito et al. (2017a) use tri-training (Zhou & Li (2005)); feature extraction layers are used to drive three classifier sub-networks. The first two are trained on samples from the source domain, while a weight similarity penalty encourages them to learn different weights. Pseudo-labels generated for target domain samples by these source domain classifiers are used to train the final classifier to operate on the target domain.
Saito等人（2017a）使用三重训练（Zhou＆Li（2005））; 特征提取层用于驱动三个分类器子网。 前两个是针对源域中的样本进行训练的，而权重相似度的惩罚则鼓励他们学习不同的权重。 这些源域分类器为目标域样本生成的伪标签用于训练最终分类器以在目标域上运行。

Generative Adversarial Networks (GANs; Goodfellow et al. (2014)) are unsupervised models that consist of a generator network that is trained to generate samples that match the distribution of a dataset by fooling a discriminator network that is simultaneously trained to distinguish real samples from generates samples. Some GAN based models – such as that of Sankaranarayanan et al. (2017) – use a GAN to help learn a domain invariant embedding for samples. Many GAN based domain
adaptation approaches use a generator that transforms samples from one domain to another.
生成对抗网络（GANs; Goodfellow等人（2014））是无监督模型，由受训生成器网络组成的生成器网络组成，该网络通过欺骗鉴别器网络来生成与数据集分布相匹配的样本，鉴别器网络同时受过训练以区分真实样本与生成者 样品。 一些基于GAN的模型（例如Sankaranarayanan等人（2017）的模型）使用GAN来帮助学习样本的域不变嵌入。 许多基于GAN的域自适应方法都使用将样本从一个域转换到另一个域的生成器。

Bousmalis et al. (2017) propose a GAN that adapts synthetic images to better match the characteristics of real images. Their generator takes a synthetic image and noise vector as input and produces an adapted image. They train a classifier to predict annotations for source and adapted samples alonside the GAN, while encouraing the generator to preserve aspects of the image important for annotation. The model of Shrivastava et al. (2017) consists of a refiner network (in the place of
a generator) and discriminator that have a limited receptive field, limiting their model to making local changes while preserving ground truth annotations. The use of refined simulated images with corresponding ground truths resulted in improved performance in gaze and hand pose estimation.
Bousmalis等人（2017）提出了一种GAN，它可以适应合成图像以更好地匹配真实图像的特征。 他们的生成器将合成图像和噪声矢量作为输入，并生成自适应图像。 他们训练一个分类器来预测GAN旁边的源和适应样本的注释，同时鼓励生成器保留对注释重要的图像方面。 Shrivastava等人（2017）的模型由一个精炼网络（代替发电机）和鉴别器组成，它们的接收场有限，将其模型限制为进行局部更改，同时保留地面真相注释。 使用具有相应地面真实性的精炼模拟图像可提高凝视和手势估计的性能。

Russo et al. (2017) present a bi-directional GAN composed of two generators that transform samples from the source to the target domain and vice versa. They transform labelled source samples to the target domain using one generator and back to the source domain with the other and encourage the network to learn label class consistency. This work bears similarities to CycleGAN, by Zhu et al.(2017).
Russo等人（2017）提出了由两个生成器组成的双向GAN，该生成器将样本从源域转换到目标域，反之亦然。 他们使用一个生成器将标记的源样本转换为目标域，然后使用另一个生成器将其转换回源域，并鼓励网络学习标记类的一致性。 这项工作与Zhu等人（2017）的CycleGAN有相似之处。

A number of domain adaptation models maximise domain confusion by minimising the difference between the distributions of features extracted from source and target domains. Deep CORAL Sun & Saenko (2016) minimises the difference between the feature covariance matrices for a mini-batch of samples from the source and target domains. Tzeng et al. (2014) and Long et al. (2015) minimise the Maximum Mean Discrepancy metric Gretton et al. (2012). Li et al. (2016) described adaptive batch normalization, a variant of batch normalization (Ioffe & Szegedy (2015)) that learns separate batch normalization statistics for the source and target domains in a two-pass process, establishing new state-of-the-art results. In the first pass standard supervised learning is used to train a classifier for samples from the source domain. In the second pass, normalization statistics for target domain samples are computed for each batch normalization layer in the network, leaving the network weights as they are.
许多域自适应模型通过最小化从源域和目标域提取的特征的分布之间的差异，使域混淆最大化。 Deep CORAL Sun＆Saenko（2016）最小化了来自源域和目标域的小批量样本的特征协方差矩阵之间的差异。 Tzeng等人（2014）和Long等人（2015）最小化了最大平均差异度量Gretton等人（2012）。 Li等人（2016）描述了自适应批量归一化，这是批量归一化的一种变体（Ioffe＆Szegedy（2015）），它在两次通过过程中学习了源域和目标域的单独批量归一化统计信息，从而建立了新的状态 艺术成果。 在第一遍中，标准监督学习用于训练来自源域的样本的分类器。 在第二遍中，为网络中的每个批处理归一化层计算目标域样本的归一化统计量，而网络权重保持不变。

METHOD

Our model builds upon the mean teacher semi-supervised learning model of Tarvainen & Valpola (2017), which we will describe. Subsequently we will present our modifications that enable domain adaptation.
我们的模型建立在Tarvainen＆Valpola（2017）的平均教师半监督学习模型的基础上，我们将对此进行描述。 随后，我们将介绍实现域自适应的修改。

The structure of the mean teacher model of Tarvainen & Valpola (2017) – also discussed in section 2.1 – is shown in Figure 2a. The student network is trained using gradient descent, while the weights of the teacher network are an exponential moving average of those of the student. During training each input sample xi is passed through both the student and teacher networks, generating predicted class probability vectors zi (student) and z~i (teacher). Different dropout, noise and image translation parameters are used for the student and teacher pathways.
Tarvainen＆Valpola（2017）的平均教师模型的结构（也在第2.1节中进行了讨论）如图2a所示。 使用梯度下降训练学生网络，而教师网络的权重是学生的指数移动平均值。 在训练期间，每个输入样本xi都通过学生和教师网络，生成预测的班级概率向量zi（学生）和z〜i（教师）。 不同的辍学，噪声和图像翻译参数用于学生和教师的途径。

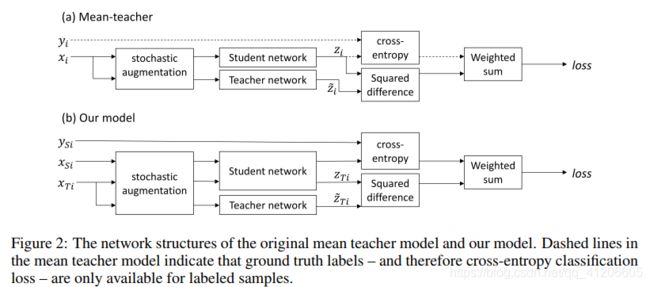
During each training iteration a mini-batch of samples is drawn from the dataset, consisting of both labeled and unlabeled samples. The training loss is the sum of a supervised and an unsupervised component. The supervised loss is cross-entropy loss computed using zi (student prediction). It is masked to 0 for unlabeled samples for which no ground truth is available. The unsupervised component is the self-ensembling loss. It penalises the difference in class predictions between student (zi) and teacher (z~i) networks for the same input sample. It is computed using the mean squared difference between the class probability predictions zi and z~i.
在每次训练迭代期间，从数据集中抽取一小批样本，其中包括标记样本和未标记样本。 训练损失是有监督和无监督部分的总和。 监督损失是使用zi（学生预测）计算的交叉熵损失。 对于没有基础真相的未标记样本，它将被屏蔽为0。 无监督的成分是自聚集损失。 对于相同的输入样本，它惩罚了学生（zi）和教师（z〜i）网络之间的班级预测差异。 它是使用类别概率预测zi和z〜i之间的均方差来计算的。
Laine & Aila (2017) and Tarvainen & Valpola (2017) found that it was necessary to apply a timedependent weighting to the unsupervised loss during training in order to prevent the network from getting stuck in a degenerate solution that gives poor classification performance. They used a function that follows a Gaussian curve from 0 to 1 during the first 80 epochs.
Laine＆Aila（2017）和Tarvainen＆Valpola（2017）发现，有必要对训练过程中的无监督损失应用时间依赖性加权，以防止网络陷入退化的解决方案中，从而导致分类性能不佳。 他们使用了一个函数，该函数在前80个时期内遵循从0到1的高斯曲线。

In the following subsections we will describe our contributions in detail along with the motivations for introducing them.
在以下小节中，我们将详细描述我们的贡献以及引入它们的动机。

ADAPTING TO DOMAIN ADAPTATION适应域适应
We minimise the same loss as in Tarvainen & Valpola (2017); we apply cross-entropy loss to labeled source samples and unsupervised self-ensembling loss to target samples. As in Tarvainen & Valpola (2017), self-ensembling loss is computed as the mean-squared difference between predictions produced by the student (zT i) and teacher (z~T i) networks with different augmentation, dropout and noise parameters.
我们将与Tarvainen＆Valpola（2017）中相同的损失降至最低; 我们将交叉熵损失应用于标记的源样本，并将无监督的自组装损失应用于目标样本。 与Tarvainen＆Valpola（2017）一样，自整合损失的计算方法是学生（zT i）和教师（z〜T i）网络在具有不同的增强，衰减和噪声参数的情况下产生的预测之间的均方差。
The models of Tarvainen & Valpola (2017) and of Laine & Aila (2017) were designed for semisupervised learning problems in which a subset of the samples in a single dataset have ground truth labels. During training both models mix labeled and unlabeled samples together in a minibatch. In contrast, unsupervised domain adaptation problems use two distinct datasets with different underlying distributions; labeled source and unlabeled target. Our variant of the mean teacher model – shown in Figure 2b – has separate source (XSi) and target (XT i) paths. Inspired by the work of Li et al. (2016), we process mini-batches from the source and target datasets separately (per iteration) so that batch normalization uses different normalization statistics for each domain during training.1.We do not use the approach of Li et al. (2016) as-is, as they handle the source and target datasets separtely in two distinct training phases, where our approach must train using both simultaneously.We also do not maintain separate exponential moving averages of the means and variances for each dataset for use at test time.
Tarvainen＆Valpola（2017）和Laine＆Aila（2017）的模型设计用于半监督学习问题，其中单个数据集中的样本子集具有地面真实性标签。在训练过程中，两个模型都将标记和未标记的样本混合在一起进行小批量处理。相反，无监督域适应问题使用具有不同基础分布的两个不同数据集。标记来源和未标记目标。我们的平均教师模型变体（如图2b所示）具有单独的源（XSi）和目标（XT i）路径。受Li等人（2016）的启发，我们从源数据集和目标数据集分别处理了迷你批处理（每次迭代），以便在训练过程中批量归一化对每个域使用不同的归一化统计数据1。 Li等人（2016）的现状，因为它们在两个不同的训练阶段分别处理源数据集和目标数据集，在这种情况下，我们的方法必须同时使用这两个方法进行训练。我们也没有保持均值和方差的指数移动平均值在测试时使用的每个数据集。
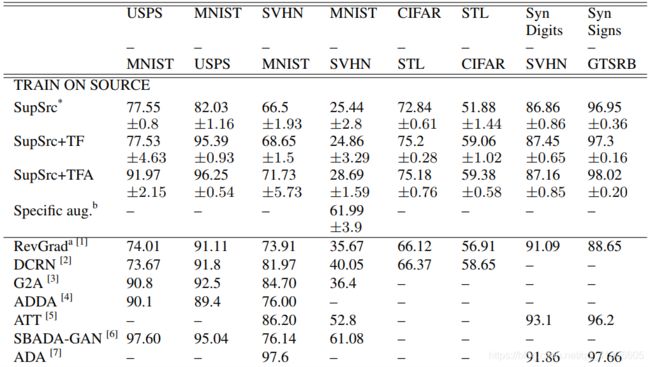
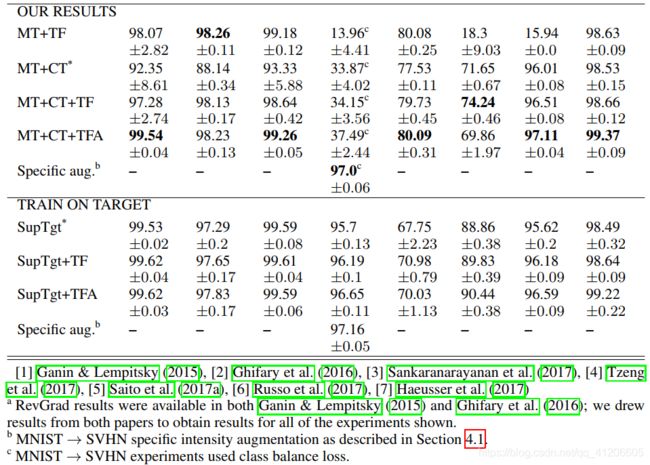
As seen in the ‘MT+TF’ row of Table 1, the model described thus far achieves state of the art results in 5 out of 8 small image benchmarks. The MNIST -> SVHN, STL ->CIFAR-10 and Syn-digits -> SVHN benchmarks however require additional modifications to achieve good performance.
如表1的“ MT + TF”行所示，到目前为止，描述的模型在8个小图像基准测试中有5个达到了最新水平。 但是，MNIST-> SVHN，STL-> CIFAR-10和Syn-digits-> SVHN基准需要进行其他修改才能获得良好的性能。

CONFIDENCE THRESHOLDING信心阈值
我们发现，在更具挑战性的域适应方案中，用置信阈值稳定训练代替了可缩放无监督损失的高斯上升因子。 对于每个未标记的样本xT i，教师网络都会生成预测的班级概率向量z〜T ij-其中j是从班级C集合中得出的班级索引-我们从中计算置信度f〜T i = maxj2C（〜zT ij ）; 样本预测类别的预测概率。 如果f〜T i低于置信度阈值（参数搜索发现0.968是小图像基准的有效值），则样本xi的自聚集损耗被掩码为0。

Our working hypothesis is that confidence thresholding acts as a filter, shifting the balance in favour of the student learning correct labels from the teacher. While high network prediction confidence does not guarantee correctness there is a positive correlation. Given the tolerance to incorrect labels reported by Laine & Aila (2017), we believe that the higher signal-to-noise ratio underlies the success of this component of our approach.
我们的工作假设是置信度阈值充当过滤器，使平衡发生变化，有利于学生从老师那里学习正确的标签。 尽管较高的网络预测置信度不能保证正确性，但存在正相关。 鉴于Laine＆Aila（2017）报告的对不正确标签的容忍度，我们认为较高的信噪比是我们此方法成功的基础。
The use of confidence thresholding achieves a state of the art results in the STL -> CIFAR-10 and Syn-digits -> SVHN benchmarks, as seen in the ‘MT+CT+TF’ row of Table 1. While confidence thresholding can result in very slight reductions in performance (see the MNIST <-> USPS and SVHN -> MNIST results), its ability to stabilise training in challenging scenarios leads us to recommend it as a replacement for the time-dependent Gaussian ramp-up used in Laine & Aila (2017).
如表1的“ MT + CT + TF”行所示，置信度阈值的使用在STL-> CIFAR-10和Syn-digits-> SVHN基准测试中获得了最先进的结果。 在性能略有降低的情况下（请参见MNIST <-> USPS和SVHN-> MNIST结果），其在挑战性场景中稳定训练的能力使我们推荐它替代Laine中使用的时间依赖性高斯加速 ＆艾拉（2017）。

DATA AUGMENTATION数据扩充
We explored the effect of three data augmentation schemes in our small image benchmarks (section 4.1). Our minimal scheme (that should be applicable in non-visual domains) consists of Gaussian noise (with σ = 0.1) added to the pixel values. The standard scheme (indicated by ‘TF’ in
Table 1) was used by Laine & Aila (2017) and adds translations in the interval [−2, 2] and horizontal flips for the CIFAR-10 <-> STL experiments. The affine scheme (indicated by ‘TFA’) adds random affine transformations defined by the matrix in (1), where N(0; 0.1) denotes a real value
drawn from a normal distribution with mean 0 and standard deviation 0.1.
我们在小型图像基准测试中探索了三种数据增强方案的效果（第4.1节）。 我们的最小方案（应适用于非视觉域）由添加到像素值的高斯噪声（σ= 0.1）组成。 Laine＆Aila（2017）使用了标准方案（在表1中以“ TF”表示），并为CIFAR-10 <-> STL实验添加了间隔[−2，2]和水平翻转的转换。 仿射方案（用“ TFA”表示）添加了由（1）中的矩阵定义的随机仿射变换，其中N（0; 0.1）表示从均值0和标准偏差为0.1的正态分布得出的实数值。
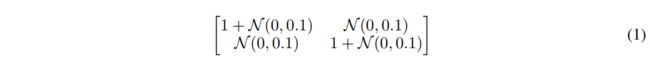The use of translations and horizontal flips has a significant impact in a number of our benchmarks. It is necessary in order to outpace prior art in the MNIST <-> USPS and SVHN -> MNIST benchmarks and improves performance in the CIFAR-10 <-> STL benchmarks. The use of affine augmentation can improve performance in experiments involving digit and traffic sign recognition datasets, as seen in the ‘MT+CT+TFA’ row of Table 1. In contrast it can impair performance when used with photographic datasets, as seen in the the STL -> CIFAR-10 experiment. It also impaired performance in the VisDA-17 experiment (section 4.2).
平移和水平翻转的使用对我们的许多基准产生了重大影响。 为了赶超MNIST-> USPS和SVHN-> MNIST基准中的现有技术，并提高CIFAR-10 <-> STL基准中的性能，这是必要的。 仿射增强的使用可以改善涉及数字和交通标志识别数据集的实验的性能，如表1的“ MT + CT + TFA”行所示。相反，与照片数据集一起使用时，仿射可以削弱性能，如表1所示。 STL-> CIFAR-10实验。 它还会损害VisDA-17实验的性能（4.2节）。
CLASS BALANCE LOSS等级平衡损失
With the adaptations made so far the challenging MNIST -> SVHN benchmark remains undefeated due to training instabilities. During training we noticed that the error rate on the SVHN test set decreases at first, then rises and reaches high values before training completes. We diagnosed the problem by recording the predictions for the SVHN target domain samples after each epoch. The rise in error rate correlated with the predictions evolving toward a condition in which most samples are
predicted as belonging to the ‘1’ class; the most populous class in the SVHN dataset. We hypothesize that the class imbalance in the SVHN dataset caused the unsupervised loss to reinforce the ‘1’ class more often than the others, resulting in the network settling in a degenerate local minimum. Rather than distinguish between digit classes as intended it seperated MNIST from SVHN samples and assigned the latter to the ‘1’ class.
到目前为止，由于训练的不稳定性，经过不断的修改，具有挑战性的MNIST-> SVHN基准仍然不败。 在训练过程中，我们注意到SVHN测试集的错误率先下降，然后上升并达到高值，然后训练完成。 我们通过在每个时期后记录SVHN目标域样本的预测来诊断问题。 错误率的上升与预测的发展趋势有关，在这种情况下，大多数样本被预测为“ 1”类； SVHN数据集中人口最多的类。 我们假设SVHN数据集中的类别不平衡会导致无监督的损失比其他类别更频繁地强化“ 1”类别，从而导致网络陷入退化的局部最小值。 与其按预期区分数字类，不如将MNIST与SVHN样本分开，并将后者分配给“ 1”类。
We addressed this problem by introducing a class balance loss term that penalises the network for making predictions that exhibit large class imbalance. For each target domain mini-batch we compute the mean of the predicted sample class probabilities over the sample dimension, resulting in the mini-batch mean per-class probability. The loss is computed as the binary cross entropy between the mean class probability vector and a uniform probability vector. We balance the strength of the class balance loss with that of the self-ensembling loss by multiplying the class balance loss by the average of the confidence threshold mask (e.g. if 75% of samples in a mini-batch pass the confidence threshold, then the class balance loss is multiplied by 0.75).
我们通过引入类平衡损失术语来解决此问题，该术语会惩罚进行较大类不平衡预测的网络。 对于每个目标域迷你批次，我们计算样本维度上预测样本类别概率的平均值，从而得出迷你批次平均每类别概率。 将损失计算为均值类别概率向量和均匀概率向量之间的二进制交叉熵。 通过将类平衡损失乘以置信度阈值掩码的平均值，我们可以平衡类平衡损失与自组装损失的强度（例如，如果微型批次中的75％的样本通过了置信度阈值，则 类别余额损失乘以0.75）。
We would like to note the similarity between our class balance loss and the entropy maximisation loss in the IMSAT clustering model of Hu et al. (2017); IMSAT employs entropy maximisation to encourage uniform cluster sizes and entropy minimisation to encourage unambiguous cluster
assignments.
我们要指出的是，Hu et al（2017）的IMSAT聚类模型中类平衡损失与熵最大化损失之间的相似性; IMSAT利用熵最大化来鼓励统一的簇大小，并利用熵最小化来促进明确的簇分配。

EXPERIMENTS

CONCLUSIONS

We have presented an effective domain adaptation algorithm that has achieved state of the art results in a number of benchmarks and has achieved accuracies that are almost on par with traditional supervised learning on digit recognition benchmarks targeting the MNIST and SVHN datasets. The resulting networks will exhibit strong performance on samples from both the source and target domains. Our approach is sufficiently flexible to be usable for a variety of network architectures, including those based on randomly initialised and pre-trained networks.
我们提出了一种有效的域自适应算法，该算法在许多基准测试中均达到了最新水平，并且其精度几乎与针对MNIST和SVHN数据集的数字识别基准测试的传统监督学习相当。 由此产生的网络将在来自源域和目标域的样本上展现出强大的性能。 我们的方法足够灵活，可用于各种网络架构，包括基于随机初始化和预训练网络的架构。

Miyato et al. (2017) stated that the self-ensembling methods presented by Laine & Aila (2017) – on which our algorithm is based – operate by label propagation. This view is supported by our results,in particular our MNIST -> SVHN experiment. The latter requires additional intensity augmentation in order to sufficiently align the dataset distributions, after which good quality label predictions are propagated throughout the target dataset. In cases where data augmentation is insufficient to align the dataset distributions, a pre-trained network may be used to bridge the gap, as in our solution to the VisDA-17 challenge. This leads us to conclude that effective domain adaptation can be achieved by first aligning the distributions of the source and target datasets – the focus of much prior art in the field – and then refining their correspondance; a task to which self-ensembling is well suited.
Miyato等人（2017年）指出，Laine＆Aila（2017年）提出的自组装方法（我们的算法基于该方法）通过标签传播进行操作。 我们的结果，尤其是我们的MNIST-> SVHN实验，支持了这种观点。 后者需要额外的强度增强以充分对齐数据集分布，然后在整个目标数据集中传播高质量的标签预测。 在数据扩充不足以对齐数据集分布的情况下，可以像在我们解决VisDA-17挑战的解决方案中那样，使用经过预训练的网络来缩小差距。 这使我们得出结论，有效的领域适应可以通过首先对齐源数据集和目标数据集的分布（本领域许多现有技术的重点），然后完善它们的对应关系来实现。 自组装非常适合的任务。