清风数学建模代码笔记1（正课

1.层次分析法

2.TOPSIS

3.插值算法

埃尔米特插值

分段三次埃尔米特插值：

y_hat = pchip(x,y,x_hat)【matlab】

三次样条插值

y_hat = spline(x,y,x_hat)【matlab】

4.拟合（min loss）

matlab

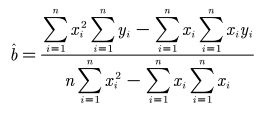
线性最小二乘法求解：

k = (n*sum(x.*y)-sum(x)*sum(y)) /(n*sum(x.*x)-sum(x)*sum(x))

b = (sum(x.*x)*sum(y)-sum(x)* sum(x.*y))/(n*sum(x.*x)-sum(x) *sum(x))

评价拟合好坏：

y_hat = k*x+b; % y 的拟合值

SSR = sum((y_hat-mean(y)).^2) % 回归平方和

SSE = sum((y_hat-y).^2) % 误差平方和

SST = sum((y-mean(y)).^2) % 总体平方和

SST-SSE-SSR

R_2 = SSR / SST

 ps：使用R^2是在线性函数时，比较线性函数与其他类型看SSE即可

 拟合工具箱

 APP->Curve Fitting

置信区间为所求得参数范围，拟合的方法有多种，还可以自定义

 5.相关系数

描述性统计

对数据进行描述性统计：

MIN = min(Test); % 每一列的最小值

MAX = max(Test); % 每一列的最大值

MEAN = mean(Test); % 每一列的均值

MEDIAN = median(Test); % 每一列的中位数

SKEWNESS = skewness(Test); % 每一列的偏度

KURTOSIS = kurtosis(Test); % 每一列的峰度

STD = std(Test); % 每一列的标准差

RESULT = [MIN;MAX;MEAN;MEDIAN;SKEWNESS;KURTOSIS;STD]

excel：数据->数据分析->描述分析

SPSS：分析->描述统计->描述

皮尔逊相关系数

首先你要确定两个变量之间是线性的关系，之后才可以用皮尔逊相关系数看他们的相关系数（可以通过画散点图：

计算相关系数：[R,P] = corrcoef(Test)   R为相关系数表，P为每个相关系数的p值

对皮尔逊相关系数进行假设检验

原假设：相关系数不显著异于0

 通过[R,P] = corrcoef(Test) 的P矩阵，如果其小于0.05，则在95%的概率下拒绝原假设，即相关系数显著异于0

皮尔逊相关系数的条件

要想使用皮尔逊相关系数，首先得保证数据为正态分布：

JB检验：（n>30)

[h,p] = jbtest(x,alpha)    当输出h等于1时，表示拒绝原假设；h等于0则代表不能拒绝原假设。 

alpha 就是显著性水平，一般取 0.05 ，此时置信水平为 1‐0.05=0.95

Shapiro-wilk检验（n位于3-50间）

使用SPSS：

斯皮尔曼相关系数

斯皮尔曼相关系数被定义成 等级之间的皮尔逊相关系数

(1 ） corr(X , Y , 'type' , 'Spearman')

这里的 X 和 Y 必须是列向量哦 ~

(2 ） corr(X , 'type' , 'Spearman')

斯皮尔曼假设性检验

 小样本直接查表（n<=30)

大样本：算其p值

 综述

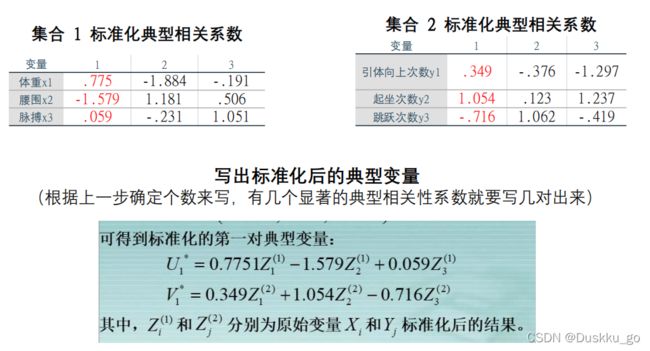
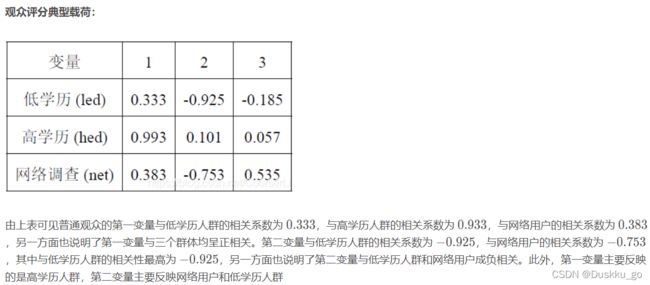
 6.典型相关分析

SPSS：导入数据->调整变量类型->分析->相关->典型相关性

结果分析：

当显著性<0.05时表示在95%的置信水平下相关性有效（不有效的直接排除）

典型在和分析可以看一下这个解释

 7.多元线性回归分析

描述性统计

使用Stata

【数据描述性统计也可以用excel中的数据透视表】

导入数据->sum ***描述性统计定量数据->tab ***，gen（A）描述定性数据并产生虚拟变量

 保存代码：

进行回归分析

reg 自变量 因变量1 因变量2....（定性数据要以虚拟变量的形式加入）【另外stata会自动解决数据完全多重共线性的问题，即将虚拟变量组合当中的一个作为对照】

 如果想看哪个变量对因变量影响最大：(标准化

reg y x1 x2 ,b

 异方差检验：

即原假设为存在异方差 

在reg之后：

1.BP检验   estat hettest ,rhs iid

2.怀特检验：estat imtest,white

 异方差处理

（ 1 ）使用 OLS +  稳健的标准误

   regress y x1 x2 … xk,robust

检查多重共线性

Stata 计算各自变量 VIF 的命令（在回归结束后使用）：

estat vif

 解决多重共线性

可以pe  r  b等同时使用

 综述

先进行数据的描述性统计->reg看prob>F是否小于0.05->异方差检验->（解决）->多重共线性检验->（解决）

8.图论最短路径问题

 无向图graph，有向图digraph

计算最短路径：[P,d] = shortestpath(G,start,end [,'Method',algorithm] )    【method不指定的话会自动认定】

任意两点间距离矩阵：d = distances(G [,'Method',algorithm])

距离某一个点为x的点及距离：[nodeIDs,dist] = nearest(G,s,d [,'Method',algorithm])

9.分类模型

二分类

逻辑回归

1.提前对数据进行处理（如类A设置为1，B为0）或在SPSS中设置虚拟变量

 2.逻辑回归利用sigmoid函数作为激活函数

 下表可以看出预测的准确率

 下表中的B即为函数当中的参数β

 如果预测结果较差，可以加入平方项、交互项等：

 确定合适的模型：将数据分为训练集和测试集（反复分）用训练集进行训练，测试集进行测试

 Fisher（LDA）

 下表中典则判别函数系数即为超平面wx=0的w，分类函数系数见图

 多分类问题

Fisher

不同于二分类的是，将范围写成对应的数字（如分类1234，则最小值1最大值4）

逻辑回归

10.聚类 

K-means与K-means++

SPSS（++的区别就是聚类中心是轮盘法选出）

 当各个值之间的量纲不同时：

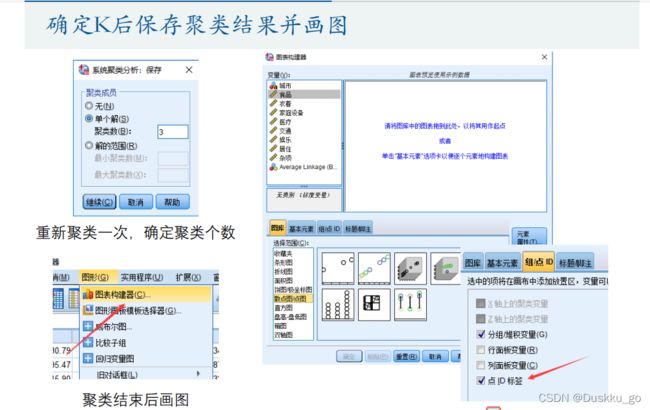
系统层次聚类算法

 

 其中最后一个阶段有一个类，29阶段2个....第一个阶段就是n-1，其中的系数就是所有类的总畸变程度（可用来画肘部图，依次来估计最优的聚类数目）【先对其降序排序然后画散点图】

 另外如果指标数比较少的时候还可以画图（例如两个指标就可以画一个二维图，三个就可以三维图，更高维不可以做图）

 

 DBSCAN（基于密度）

代码见资料

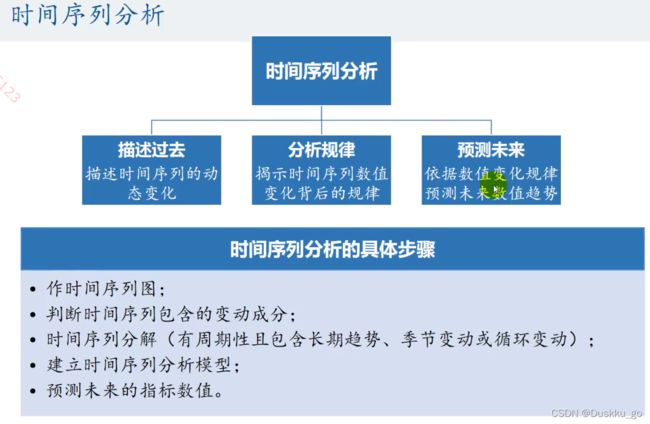
11.时间序列分析

数据缺失值处理

如果是开头或者结尾的数据可以直接删除，中间的数据需要利用spss对其处理

 季节分解模型

 定义时间变量

时间序列图

季节性分析

 产生的四个变量ERR、SAS、SAF、STC，季节性因子即SAF

 

 之后再画时序图要加上新产生的四个变量，可以根据这四个变量的图像合理拟合等再组合产生对于y的预测

时间序列分析步骤

实例

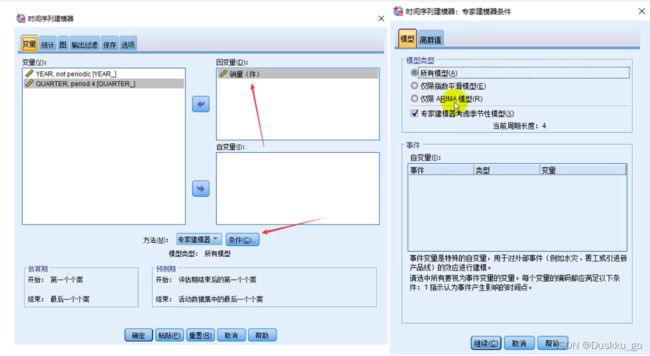
SPSS时间序列建模思路

创建模型

离群值全部勾选，选项那一部分是你想预测到什么时候

 

 

 

 

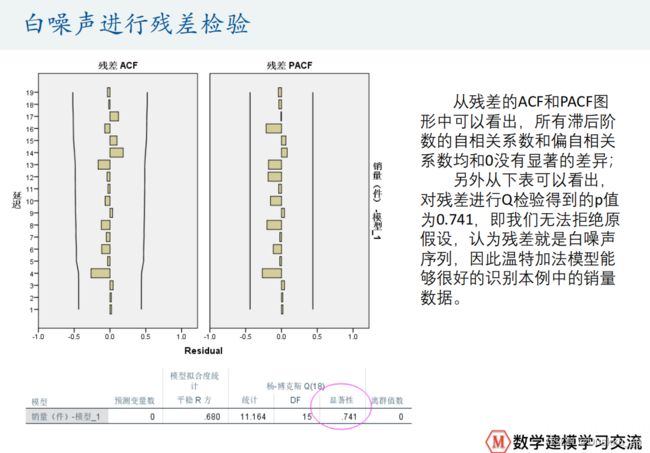
结果分析

 

 

 

12.预测模型

灰色预测：gm11，新信息gm11，新陈代谢gm11

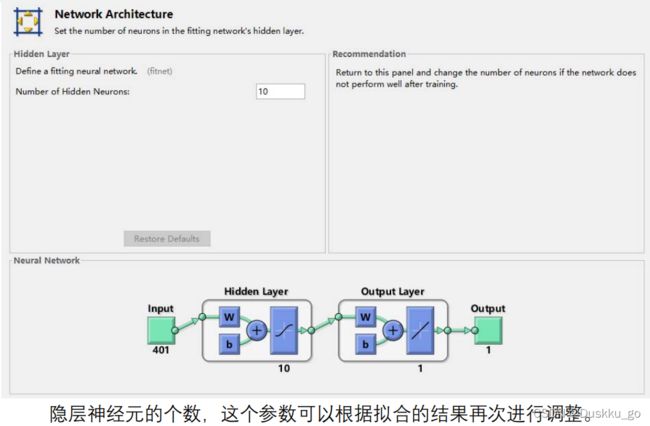
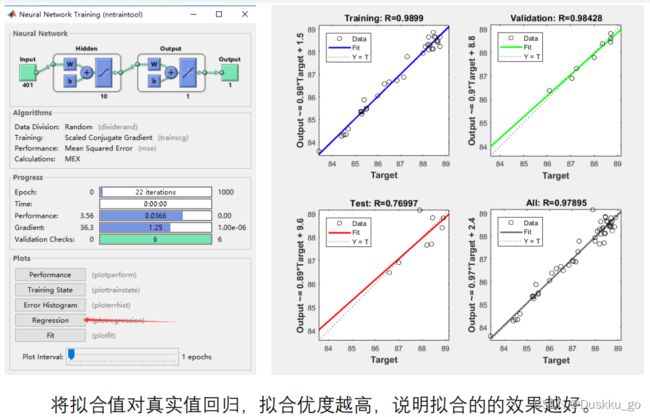
神经网络

选择模型进行训练

 

 

 

 结果分析

 （小绿圈是均方误差最小的时候所在位置）

 保存结果

 

 为了防止过拟合可以将数据分成训练集和测试集，通过调整神经元数量以及训练方法，使得SSEmin，之后再对新数据进行预测。

13.SVD及对图片视频的处理【降维】

14.主成分分析（可用于聚类、回归）

主成分分析是一种降维算法，它能将多个指标转换为少数几个主成分，这些主成分是原始变量的线性组合，且彼此之间 互不相关，其能反映出原始数据的大部分信息。一般来说， 当研究的问题涉及到多变量且变量之间存在很强的相关性时， 我们可考虑使用主成分分析的方法来对数据进行简化。

例子+matlab

1.计算相关系数矩阵

corrcoef计算相关系数矩阵，不用判断p（将标准化+协方差矩阵合二为一，z标准化：zscore，协方差：cov）

 2.根据累计贡献率判断关键变量

matlab中求的特征向量自动进行了归一化处理，diag返回主对角线元素

 3.写出主成成分并简要分析

 4.说明

 用于聚类

主成分聚类最大的意义就是能帮我们可视化最后的聚类效果，毕竟， 使用主成分是会降低部分息的。言外之意，只有在指标个数特别多，且指标 之间存在很强的相关性时才用主成分聚类。

用于回归

芜湖完结~接下来学习更新视频~